Тема 2.7. Расчёты на прочность при сложном напряжённом состоянии. 1 страница

Для заметок.

2.7.1. Напряжённое состояние в точке. Типы напряжённого состояния.

2.7.2. Линейное напряжённое состояние.

2.7.3. Плоское напряжённое состояние.

2.7.4. Объёмное напряжённое состояние.

2.7.5. Определение главных напряжений при плоском напряжённом состоянии.

2.7.6. Гипотезы предельных напряжённых состояний (гипотезы прочности).

2.7.7. Косой изгиб.

2.7.8. Изгиб с растяжением (сжатием) бруса большой жёсткости. Внецентренное растяжение (сжатие).

2.7.9. Изгиб с кручением брусьев круглого поперечного сечения.

2.7.1. Для расчета бруса на прочность при растяжении, сжатии, срезе, кручении, изгибе обычно достаточно уметь опреде­лять напряжения в поперечном сечении. При сложных ви­дах деформации бруса или при расчете элементов конструк­ций сложной формы необходимо устанавливать напряжен­ное состояние в точке. В п. 2.1.5. показано, что нельзя оп­ределить напряжение в точке тела, не указав положения сечения (площадки), проведенной через данную точку. Так как через точку можно провести бесчисленное множество се­чений, то и напряжений, по ним действующих, существует бесчисленное множество.

Совокупность всех напряжений, действующих по площадкам, прове­денным через данную точку, называют напряженным состоянием в точке.

Чтобы выявить напряженное состояние в точке тела, в ее окрестности выделяют бесконечно малый параллелепипед с длинами сторон dx, dy, dz. Можно представить, что при уменьшении размеров этого параллелепипеда он стягивает­ся в точку. Таким образом, под точкой тела в сопротивлении материалов понимают бесконечно малый объем (параллеле­пипед), выделенный в окрестности точки.

В общем случае по граням параллелепипеда действуют напряжения, показанные на рисунке 2.7.1. Напряжения по­казаны только на видимых гранях, очевидно из условий равновесия, что такие же напряжения возникают на невиди­мых гранях. Нормальные напряжения растяжения считают положительными, сжатия — отрицательными.

При повороте параллелепипеда значения всех напряже­ний, действующих на его гранях, изменяются. Можно вы­брать такое положение параллелепипеда, при котором на его гранях возникают только нормальные напряжения (каса­тельные напряжения равны нулю). Площадки, по которым действуют только нормальные напряжения, называют глав­ными. Нормальные напряжения, действующие по главным площадкам, также называют главными. Главные напряже­ния обозначают 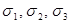. Наибольшее (с учетом знака) глав­ное напряжение обозначают 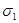, наименьшее 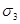. Напряжен­ное состояние в точке тела считают полностью известным, если известны напряжения на любых трех взаимно перпен­дикулярных площадках, например главных. Удобнее выби­рать такие площадки, для которых наиболее просто опреде­ляются напряжения. Обычно определяют положение глав­ных площадок и значения главных напряжений.

В общем случае главные напряжения могут действовать в направлении всех трех координатных осей (рис. 2.7.2. Б). Та­кое напряженное состояние называют трехосным или объ­емным. Главные напряжения могут быть как положитель­ными, так и отрицательными. В объемном напряженном состоянии находится, например, материал в зоне контакта двух тел (рис.2.7.2. А).

Напряженное состояние, при котором главные напряже­ния действуют в направлении двух осей, называют двухосным или плоским (рис. 2.7.3. А). Двухосное напряженное со­стояние возникает, например, в стенке тонкостенного сосуда, находящегося под давлением газа или жидкости (рис. 2.7.3. Б),при чистом сдвиге.

Напряженное состояние, при котором главное напряжение действует в направлении одной оси (два других главных напряжения равны нулю), называют одноосным или линейным (рис. 2.7.4. А). Такое напряженное состояние возникает в убрусе при растяжении (рис. 2.7.4. Б), сжатии и чистом изгибе (рис. 2.7.4. В).

Исследуем различные типы напряженного состояния с тем,чтобы получить зависимости между главными напряжениями и напряжениями в точке, действующими по любой, проведенной через нее площадке. Эти зависимости позволят определять наибольшие значения нормальных и касательных напряжений в точке и положение площадок, по кото­рым они действуют.

2.7.2. Выделим в окрестности какой-либо точки растянутого бруса бесконечно малый параллелепипед так, чтобы две его грани совпадали с поперечными сечениями (см. рис. 2.7.4. Б). В теме 2.2. показано, что на гранях, совпадающих с поперечными сечениями, возникают только нормальные напряжения, а на гранях, параллельных оси бруса, напряжения отсутствуют (рис. 2.7.5. А). В соответствии с принятым соотношением между главными напряжениями можно обозначить

Дата добавления: 2015-06-30