
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 2.7. Расчёты на прочность при сложном напряжённом состоянии. 2 страница
|
|
|
|
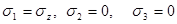 .
.
 Зная напряжение
Зная напряжение 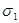 , можно определить нормальное и касательное напряжения, действующие по любой площадке, проведенной через точку:
, можно определить нормальное и касательное напряжения, действующие по любой площадке, проведенной через точку:
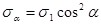 ,
, 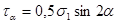 , (2.7.1.)
, (2.7.1.)
следовательно, главное напряжение 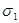 полностью определяет одноосное напряженное состояние в точке.
полностью определяет одноосное напряженное состояние в точке.
Разновидностью рассмотренного одноосного напряженного состояния является напряженное состояние, при котором возникает одно главное напряжение 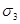 . Расчетные формулы (2.7.1.) остаются справедливыми с заменой в них
. Расчетные формулы (2.7.1.) остаются справедливыми с заменой в них 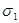 на
на 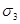 .
.
2.7.3. Выделим из элемента конструкции, находящегося в плоском напряженном состоянии, элементарный кубик (рис. 2.7.6. А). Исследуем это напряженное состояние. Проведем сечение, нормаль к которому составляет угол 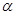 с направлением
с направлением 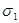 , и рассмотрим равновесие отсеченной части (рис. 2.7.6. Б). Угол
, и рассмотрим равновесие отсеченной части (рис. 2.7.6. Б). Угол 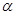 считаем положительным, если он отложен от направления
считаем положительным, если он отложен от направления 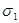 до нормали к площадке против часовой стрелки. Тогда, применив принцип независимости действия сил, получим
до нормали к площадке против часовой стрелки. Тогда, применив принцип независимости действия сил, получим
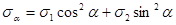 ,
, 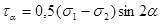 . (2.7.2.)
. (2.7.2.)
Из формул (2.7.2.):
 1) при
1) при 
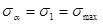 ,
, 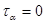 ;
;
2) при 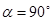
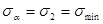 ,
, 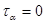 ;
;
3) при 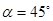
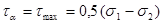 .
.
Таким образом, главные напряжения имеют наибольшее и наименьшее значения из всех нормальных напряжений, действующих по площадкам, проведённым через данную точку.
наибольшие касательные напряжения возникают на площадке, наклонённой под углом 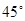 к оси бруса:
к оси бруса:

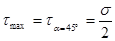 ;
;
Кроме того, касательные напряжения, возникающие на взаимно перпендикулярных площадках, равны по абсолютному значению:
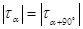 ,
,
а векторы касательных напряжений на взаимно перпендикулярных площадках должны быть направлены или к ребру, или от ребра. Данное утверждение носит название закона парности касательных напряжений.
2.7.4. Выделим в окрестности точки тела, находящегося в объемном напряженном состоянии, элементарный кубик, по граням которого действуют главные напряжения 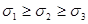 .
.
Определим нормальное и касательное напряжения для площадок, параллельных одному из главных напряжений. Из условий равновесия отсеченных такими площадками частей кубика можно установить, что действующие по площадкам напряжения не зависят от того из главных напряжений, параллельно которому проведена площадка. Следовательно, для трехосного напряженного состояния можно определять напряжения, действующие по площадкам, параллельным одному из главных напряжений, по формулам (2.7.2.), полученным для двухосного напряженного состояния.
 Наибольшее касательное напряжение при трехосном напряженном состоянии
Наибольшее касательное напряжение при трехосном напряженном состоянии

действует по площадке, параллельной 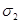 , причем нормаль к площадке составляет угол 45° с направлением
, причем нормаль к площадке составляет угол 45° с направлением 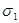 (рис. 2.7.7.).
(рис. 2.7.7.).
 2.7.5. Напряженное состояние в точке полностью известно, если известны главные напряжения. Однако при расчетах бруса, как показано ранее, определяют напряжения в поперечных сечениях. При растяжении, сжатии и чистом изгибе в поперечных сечениях бруса возникают только нормальные напряжения, а при кручении только касательные. Очевидно, при совместном действии изгиба и кручения, а также растяжения и кручения в поперечных сечениях возникают как нормальные, так и касательные напряжения. Нормальные и касательные напряжения возникают во всех точках поперечного сечения бруса (кроме крайних) также при поперечном изгибе. В продольных сечениях бруса при этом нормальных напряжений нет (рис. 2.7.8.).
2.7.5. Напряженное состояние в точке полностью известно, если известны главные напряжения. Однако при расчетах бруса, как показано ранее, определяют напряжения в поперечных сечениях. При растяжении, сжатии и чистом изгибе в поперечных сечениях бруса возникают только нормальные напряжения, а при кручении только касательные. Очевидно, при совместном действии изгиба и кручения, а также растяжения и кручения в поперечных сечениях возникают как нормальные, так и касательные напряжения. Нормальные и касательные напряжения возникают во всех точках поперечного сечения бруса (кроме крайних) также при поперечном изгибе. В продольных сечениях бруса при этом нормальных напряжений нет (рис. 2.7.8.).
Зависимость между главными напряжениями, с одной стороны, нормальными и касательными напряжениями, возникающими в поперечных сечениях бруса, — с другой имеет вид:
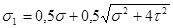 ,
,  ,
, 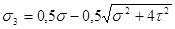 . (2.7.3.)
. (2.7.3.)
2.7.6. Нарушением прочности элемента конструкции считают появление хотя бы в одной его точке пластических деформаций или признаков хрупкого разрушения. Напряженное состояние в такой точке считают предельным.
При растяжении, сжатии и чистом изгибе напряженное состояние одноосное. Оно становится предельным, когда напряжение в точке достигает предела текучести для пластичных материалов или предела прочности для хрупких. При двухосном или трехосном напряженном состоянии в точке могут появиться пластические деформации или признаки хрупкого разрушения и напряженное состояние станет предельным, хотя значение каждого из главных напряжений меньше предела текучести или прочности. При расчете на прочность элемента конструкции необходимо знать, насколько напряженное состояние в опасной его точке отличается от предельного.
Точно на этот вопрос можно ответить, если испытать образец, изготовленный из данного материала при напряженном состоянии, подобном напряженному состоянию в опасной точке рассчитываемого элемента.
Подобными называют напряженные состояния с одинаковым соотношением главных напряжений
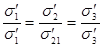
Увеличивая при испытании образца пропорционально все главные напряжения, можно заметить, при каком их значении напряженное состояние станет предельным, т. е. в образце появятся пластические деформации или признаки хрупкого разрушения.
Величину, показывающую, во сколько раз следует увеличить главные напряжения, чтобы напряженное состояние стало предельным, называют коэффициентом запаса прочности.
Такой способ оценки напряженного состояния и определения его запаса прочности практически невозможен вследствие сложности испытаний и большого разнообразия возможных соотношений главных напряжений. Так как в основном испытания материалов проводят при растяжении и сжатии, т.е. при одноосном напряженном состоянии, возникает вопрос, нельзя ли оценить прочность элементов конструкций при сложном напряженном состоянии по характеристикам прочности, полученным при растяжении или сжатии.
Такая оценка возможна с использованием гипотез предельных напряженных состояний (гипотез прочности).
Гипотезы прочности позволяют заменить сложное напряженное состояние равноопасным одноосным напряженным состоянием, возникающим при растяжении.
Равноопасными называют напряженные состояния, если они переходят в предельные при увеличении их главных напряжений в одинаковое число раз. Иначе говоря, равноопасными называют напряженные состояния, для которых равны коэффициенты запаса прочности.
Напряжение одноосного растяжения, равноопасного заданному сложному напряженному состоянию, называют эквивалентным напряжением 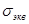 .
.
Таким образом, можно определить последовательность выполнения расчета на прочность элемента конструкции при сложном напряженном состоянии: установив положение опасной точки элемента, определить тип напряженного состояния и главные напряжения в этой точке, заменить на основе выбранной гипотезы прочности сложное напряженное состояние эквивалентным напряжением растяжения и сопоставить его с предельным напряжением (рис. 2.7.9.), равным пределу текучести или прочности при растяжении.
 При этом коэффициент запаса прочности элемента конструкции
При этом коэффициент запаса прочности элемента конструкции
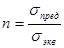 .
.
Остается выяснить, на основе какого критерия можно считать различные напряженные состояния равноопасными и как определить значение эквивалентного напряжения. Рассмотрим три наиболее широко применяемые на практике гипотезы предельных напряженных состояний, которые часто называют теориями прочности.
Гипотеза максимальных касательных напряжений. Два напряженных состояния считают равноопасными, если для них равны максимальные касательные напряжения.
При испытаниях на растяжение образцов из пластичных материалов было замечено, что разрушение происходит по сечению, наклоненному к оси образца под углом 45°. Особенно это заметно при испытаниях плоских образцов. Так как в этом сечении возникают при растяжении максимальные касательные напряжения, была высказана гипотеза (предположение) о том, что ответственными за наступление предельного состояния материала являются максимальные касательные напряжения.
Следовательно, можно заменить сложное напряженное состояние эквивалентным одноосным растяжением при условии, что для них равны 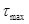 .
.
Для сложного напряженного состояния  , для эквивалентного растяжения
, для эквивалентного растяжения 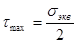 . Приравняв выражения для максимальных касательных напряжений, получим
. Приравняв выражения для максимальных касательных напряжений, получим
 . (2.7.4.)
. (2.7.4.)
Сопоставив полученное эквивалентное напряжение с допускаемым напряжением при растяжении, получим условие прочности
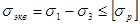 . (2.7.5.)
. (2.7.5.)
Гипотеза прочности максимальных касательных напряжений хорошо подтверждается экспериментально для пластичных материалов, имеющих одинаковые характеристики прочности при растяжении и сжатии.
Недостаток гипотезы в том, что она не учитывает влияния на прочность главного напряжения 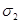 .
.
Обычно при расчетах брусьев на прочность известны не главные напряжения, а нормальное и касательное напряжения в поперечных сечениях. Подставив в формулу (2.7.4.) выражение (2.7.3.) для главных напряжений
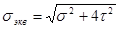 .
.
Энергетическая гипотеза прочности. Два напряженных состояния равноопасны, если для них одинаковы удельные потенциальные энергии формоизменения.
Условие прочности по энергетической гипотезе прочности принимает вид
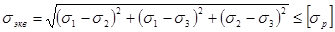 . (2.7.6.)
. (2.7.6.)
Если известны не главные напряжения, а нормальное и касательное напряжения в поперечном сечении бруса, то, подставив в (2.7.6.) выражения для 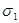 и
и 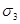 из (2.7.5.), получим
из (2.7.5.), получим
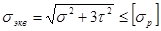 . (2.7.7.)
. (2.7.7.)
Энергетическая гипотеза прочности хорошо подтверждается экспериментально для пластичных материалов, имеющих одинаковые характеристики прочности при растяжении и сжатии.
Заметим, что в отличие от гипотезы прочности наибольших касательных напряжений (2.7.5.) условие прочности, по энергетической гипотезе (2.7.6.), включает все три главные напряжения.
Гипотеза прочности Мора. Гипотезу прочности наибольших касательных напряжений и энергетическую гипотезу прочности широко применяют в расчетной практике для пластичных материалов, но они не учитывают различия сопротивления материалов растяжению и сжатию. Для хрупких материалов, имеющих существенно различающиеся характеристики прочности при растяжении и сжатии, расчет по этим гипотезам может привести к заметным погрешностям.
На основе обобщения экспериментов, выполненных при различных типах напряженного состояния, О. Мором предложена гипотеза, учитывающая различие в сопротивлении материалов растяжению и сжатию. Условие прочности, по гипотезе Мора, имеет вид
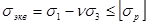 , (2.7.8.)
, (2.7.8.)
где  для пластичных материалов,
для пластичных материалов, 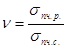 для хрупких материалов,
для хрупких материалов, 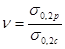 для хрупкопластичных материалов.
для хрупкопластичных материалов.
Гипотеза Мора хорошо подтверждается экспериментально как для пластичных, так и для хрупких материалов и используется в практических расчетах. При одинаковом сопротивлении материалов растяжению и сжатию  и условие прочности по гипотезе Мора совпадает с условием прочности по гипотезе наибольших касательных напряжений.
и условие прочности по гипотезе Мора совпадает с условием прочности по гипотезе наибольших касательных напряжений.
Для брусьев с известными нормальным и касательным напряжениями в поперечном сечении условие прочности (2.7.8.) с учетом выражений (2.7.3.) для главных напряжений 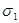 и
и 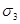 имеет вид
имеет вид
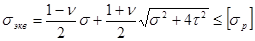 . (2.7.9.)
. (2.7.9.)
 2.7.7. Изгиб называется косым, если плоскость действия изгибающего момента, возникающего момента, возникающего в поперечном сечении бруса, не совпадает ни с одной из его главных плоскостей. Различают плоский косой изгиб (рис. 2.6.2.) и пространственный косой изгиб (рис. 2.7.10.).
2.7.7. Изгиб называется косым, если плоскость действия изгибающего момента, возникающего момента, возникающего в поперечном сечении бруса, не совпадает ни с одной из его главных плоскостей. Различают плоский косой изгиб (рис. 2.6.2.) и пространственный косой изгиб (рис. 2.7.10.).
Как плоский, так и пространственный случаи косого изгиба можно рассматривать как сочетание двух прямых изгибов в главных плоскостях инерции бруса. Все внешние силы и моменты, действующие на брус, следует разложить на составляющие по главным центральным осям его поперечного сечения и построить соответствующие эпюры изгибающих моментов 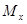 и
и 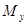 . При расчётах на прочность будем учитывать только влияние изгибающих моментов, пренебрегая влиянием поперечных сил
. При расчётах на прочность будем учитывать только влияние изгибающих моментов, пренебрегая влиянием поперечных сил 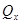 и
и 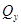 .
.
Нормальные напряжения в произвольной точке поперечного сечения определяют по формуле
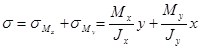 , (2.7.10.)
, (2.7.10.)
где 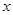 и
и  -координаты точки, в которой определяется напряжение. В формуле каждое из слагаемых должно быть подставлено со своим знаком (напряжения растяжения считают положительными). Знаки напряжений целесообразно устанавливать по характеру деформации бруса, а значения изгибающих моментов и координат точки принимать по абсолютной величине, т.е. относить знак ко всему слагаемому в целом.
-координаты точки, в которой определяется напряжение. В формуле каждое из слагаемых должно быть подставлено со своим знаком (напряжения растяжения считают положительными). Знаки напряжений целесообразно устанавливать по характеру деформации бруса, а значения изгибающих моментов и координат точки принимать по абсолютной величине, т.е. относить знак ко всему слагаемому в целом.
Для сечений (прямоугольные, двутавровые), имеющих две оси симметрии и точки одновременно наиболее удаленные от обеих главных осей, опасными являются те из угловых точек, в которых знаки напряжений 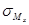 и
и 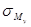 совпадают, и условие прочности имеет вид
совпадают, и условие прочности имеет вид
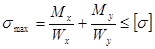 .
.
Для того, чтобы найти опасную точку поперечного сечения произвольной формы, следует в первую очередь определить положение нулевой линии этого сечения. Уравнение нулевой линии получают из выражения (2.7.10.). приравнивая нулю его правую часть,
 .
.
Наибольшие нормальные напряжения возникают в тех точках поперечного сечения, которые наиболее удалены от нулевой линии, и условие прочности имеет вид

Для бруса из хрупкого материала надо составлять условия прочности и для области растяжения и для области сжатия.
 2.7.8. Рассмотрим совместное действие на брус нагрузок, вызывающих его растяжение (сжатие) и изгиб (рис. 2.7.11.). В общем случае нагрузки, вызывающие изгиб бруса, могут действовать в различных продольных плоскостях или в одной плоскости, но не совпадающей с главной плоскостью бруса. В этом случае возникают растяжение (сжатие) и косой изгиб бруса.
2.7.8. Рассмотрим совместное действие на брус нагрузок, вызывающих его растяжение (сжатие) и изгиб (рис. 2.7.11.). В общем случае нагрузки, вызывающие изгиб бруса, могут действовать в различных продольных плоскостях или в одной плоскости, но не совпадающей с главной плоскостью бруса. В этом случае возникают растяжение (сжатие) и косой изгиб бруса.
В поперечном сечении бруса возникают продольная сила 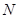 , изгибающие моменты
, изгибающие моменты 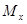 ,
, 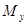 и поперечные силы
и поперечные силы 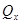 ,
, 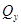 (рис. 2.7.11.).
(рис. 2.7.11.).
При сложной нагрузке, действующей на брус, когда положение опасного сечения неочевидно, строят эпюры продольной силы и изгибающих моментов. Влиянием на прочность бруса поперечных сил 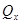 и
и 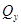 обычно пренебрегают. Если различные внутренние силовые факторы достигают наибольшего значения в различных сечениях, расчет бруса на прочность выполняют для всех предположительно опасных сечений.
обычно пренебрегают. Если различные внутренние силовые факторы достигают наибольшего значения в различных сечениях, расчет бруса на прочность выполняют для всех предположительно опасных сечений.
Напряжение в любой точке сечения бруса определяют на основании принципа независимости действия сил, как алгебраическую сумму нормальных напряжений, вызываемых каждым силовым фактором:
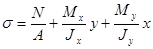 . (2.7.11.)
. (2.7.11.)
 Применение этого принципа допустимо только для бруса большой жесткости, для которого прогибы от изгибающих моментов невелики и можно пренебречь дополнительным изгибающим моментом, равным произведению растягивающей (сжимающей) силы
Применение этого принципа допустимо только для бруса большой жесткости, для которого прогибы от изгибающих моментов невелики и можно пренебречь дополнительным изгибающим моментом, равным произведению растягивающей (сжимающей) силы 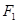 на прогиб
на прогиб 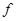 (рис. 2.7.12.).
(рис. 2.7.12.).
Опасной точкой бруса, для которой составляют условие прочности, является точка в опасном сечении, наиболее удаленная от нейтральной линии.
Положение нейтральной линии определяется уравнением, получить которое можно, приравняв нулю выражение (2.7.11.):
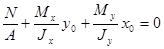 . (2.7.12.)
. (2.7.12.)
Здесь 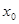 ,
, 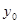 — координаты точек нейтральной линии сечения.
— координаты точек нейтральной линии сечения.
Уравнение (2.7.12.) составляют для точек, расположенных в первом квадранте сечения, т. е. для точек с положительными координатами. Знаки перед слагаемыми устанавливают с помощью правил определения знаков напряжений при растяжении (сжатии) и изгибе. Согласно уравнению (2.7.12.), нейтральная линия не проходит через начало координат (центр тяжести сечения).
Определив положение нейтральной линии сечения, можно построить эпюру нормальных напряжений. На рисунке 2.7.13. показаны эпюры напряжений  ,
, 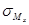 ,
, 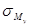 и суммарного напряжения
и суммарного напряжения 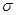 .
.
 Так как в любой точке бруса возникает только нормальное напряжение (при условии, что влиянием поперечных сил Qx и Qy можно пренебречь), напряженное состояние — одноосное, поэтому условие прочности имеет вид
Так как в любой точке бруса возникает только нормальное напряжение (при условии, что влиянием поперечных сил Qx и Qy можно пренебречь), напряженное состояние — одноосное, поэтому условие прочности имеет вид
 ,
,
Для брусьев, имеющих в опасном сечении точки, максимально удаленные от обеих главных осей инерции (например, в двутавре, прямоугольнике), опасной является угловая точка, в которой суммируются напряжения одного знака от 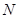 ,
, 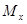 и
и 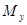 Для таких брусьев условие прочности записывают в виде
Для таких брусьев условие прочности записывают в виде
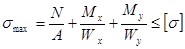 .
.
Для брусьев круглого поперечного сечения, изготовленных из пластичных материалов, положение опасной точки не определяют. Расчет на прочность выполняют по формуле
 ,
,
где 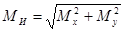 .
.
 Для брусьев, изготовленных из материалов с различным сопротивлением растяжению и сжатию (например, из чугуна), условие прочности составляют для двух опасных точек: с наибольшими напряжениями растяжения и сжатия.
Для брусьев, изготовленных из материалов с различным сопротивлением растяжению и сжатию (например, из чугуна), условие прочности составляют для двух опасных точек: с наибольшими напряжениями растяжения и сжатия.
Растяжение (сжатие) с изгибом возникает в брусе при действии только растягивающей (сжимающей) силы F, не проходящей через центр тяжести сечения. Такой вид деформации бруса называют внецентренным растяжением (сжатием) (рис. 2.7.14.).
Применим метод сечений и перенесем растягивающую (сжимающую) силу F в центр тяжести сечения (рис. 2.7.14.).Заметим, что продольная сила N равна F. В соответствии с правилами теоретической механики при параллельном переносе необходимо приложить моменты 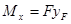 и
и 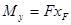 где
где  и
и 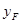 — координаты точки приложения силы.
— координаты точки приложения силы.
Таким образом, внецентренное растяжение (сжатие) есть сочетание обычного (центрального) растяжения (сжатия) и чистого изгиба.
В выражениях для изгибающих моментов отсутствует координата г, следовательно, внутренние силовые факторы во всех сечениях одинаковы и отпадает необходимость в построении их эпюр. Для бруса постоянного сечения все поперечные сечения равноопасны.
Для определения положения опасной точки сечения составляем уравнение нейтральной линии (2.7.12.), которое с учетом выражений для изгибающих моментов Мх и Му после сокращения на F принимает вид
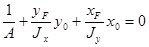 . (2.7.13.)
. (2.7.13.)
Опасной является точка, наиболее удаленная от нейтральной линии сечения, если материал бруса одинаково сопротивляется растяжению и сжатию.
Для брусьев, имеющих точки, максимально удаленные от обеих главных осей инерции х, у, положение опасной точки не определяют и условие прочности записывают в виде
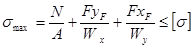 .
.
Для брусьев круглого или кольцевого поперечного сечений положение опасной точки можно не определять. Расчёт на прочность выполняют по формуле
 ,
,
где  .
.
2.7.9. Во всех машинах имеются брусья круглого или кольцевого поперечного сечения, нагруженные вращающим и изгибающим моментами. Такие брусья называют валами. На валах устанавливают вращающиеся вместе с валом детали: зубчатые колеса, шкивы, звездочки и т. д.
В общем случае для определения опасного сечения необходимо построить эпюры крутящего 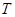 и изгибающих моментов
и изгибающих моментов 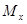 ,
, 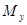 . Значение крутящего момента на участках вала, как правило, постоянно, поэтому положение опасного сечения определяют по эпюрам изгибающих моментов. Если изгибающие моменты
. Значение крутящего момента на участках вала, как правило, постоянно, поэтому положение опасного сечения определяют по эпюрам изгибающих моментов. Если изгибающие моменты 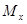 и
и 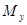 достигают наибольшего значения в различных сечениях бруса, следует вычислить для этих сечений суммарный изгибающий момент по формуле
достигают наибольшего значения в различных сечениях бруса, следует вычислить для этих сечений суммарный изгибающий момент по формуле
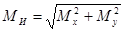 .
.
Опасным является сечение, в котором момент 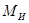 достигает наибольшего значения. Влиянием на прочность бруса (вала) поперечных сил
достигает наибольшего значения. Влиянием на прочность бруса (вала) поперечных сил 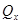 и
и 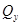 пренебрегают и их эпюры не строят.
пренебрегают и их эпюры не строят.
Рассмотрим расчет на прочность бруса круглого поперечного сечения, нагруженного вращающим и изгибающим моментами. Касательные напряжения от крутящего момента и нормальные напряжения от изгибающих моментов распределяются по сечению по линейному закону, достигая наибольшего значения в крайних точках сечения бруса.Положение опасной точки сечения не определяют, так как ее координаты не входят в расчетные формулы для 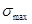 и
и  . Кроме того, валы, как правило, вращаются и все точки сечения у поверхности бруca равноопасны.
. Кроме того, валы, как правило, вращаются и все точки сечения у поверхности бруca равноопасны.
В поперечных сечениях бруса возникают напряжения
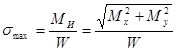 ,
, 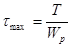 . (2.7.14.)
. (2.7.14.)
Согласно закону парности касательных напряжений, на плоскостях, параллельных оси бруса, также возникают касательные напряжения. Таким образом, в опасной точке возникает плоское напряженное состояние.
Так как напряжённое состояние не одноосное, для расчёта бруса на прочность необходимо использовать одну из гипотез прочности. Обычно валы изготавливают из среднеуглеродистых или легированных сталей, т.е. из пластичных материалов, поэтому их расчёт следует выполнять на основании гипотез прочности максимальных касательных напряжений, энергетической или Мора.
|
|
|
|
|
Дата добавления: 2015-06-30; Просмотров: 4097; Нарушение авторских прав?; Мы поможем в написании вашей работы!