Деформированию

Т. 3 СОПРОТИВЛЕНИЕ МЕТАЛЛОВ ПЛАСТИЧЕСКОМУ

Сопротивление деформации при одноосном растяжении (сжатии) σ_s – напряжение течения, т.е истинное напряжение, вызывающее стабильное пластическое течение при заданных условиях деформирования.

Величина σ_S не зависит от приложенного гидростатического давления, по крайней мере, при σ_S < 1000 МПа и если для металла справедливо условие текучести Мизеса, то сопротивление деформации при сложном напряженном состоянии есть интенсивность касательных напряжений Т_S, вызывающая стабильное пластическое течение при заданных параметрах деформирования. Так как

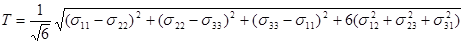
то при одноосном растяжении ; при кручении тонкостенных трубчатых образцов Т_S = τ_S, где τ_S – напряжение течения при кручении

Так как величины σ_S,Т_S,τ_S - напряжения, вызывающие стабильное пластическое течение, то устанавливают функциональную связь этих истинных напряжений с пластическими деформациями ε_пл, Г_пл и γ_пл при ОМД

путем создания общей теории определяющих уравнений, описывающих термомеханические свойства различных сплошных сред.

Тs = Тs [Тe (t)]^t_t0 или Тe = Тe [Тs (t)]^t_t0

с помощью реологических моделей, позволяющих описывать реальные термомеханические свойства деформируемых тел (реология от греческого слова «гео» — теку, наука о течении материала). Реология должна ответить на вопрос: каковы напряжения (деформации) в окрестности данной материаль­ной частицы в момент времени t при известном процессе ее деформирования (нагружения). Для теоретического решения этой задачи необходимо проведение большого объема экспериментальных исследований, основные и типичные свойства деформируемых материалов могут быть получены в опытах. Обратимся к экспериментальных исследованиях цилиндрических образцов на растяжение.

Для получения однородного напряженного и деформированного состояния в средней части образца расчетная длина l_o круглого цилиндрического об­разца должна в 5 или 10 раз превышать его диаметр d_o.

Для испытаний обычно применяют разрывные машины, позволяющие автоматически строить первичную диаграмму растяжения. В этой диаграмме по оси координат откладывают усилия Р, а по оси абсцисс — соответствующие им удлинения ∆ l.

УСЛОВНАЯ И ИСТИННАЯ ДИАГРАММА НАПРЯЖЕНИЙ. Вид диаграммы растяжения в координатах Р — ∆ l зависит не только от свойств материала, но и от размеров испытуемого об­разца. Чтобы получить диаграмму, характеризующую только механические свойства материала, первичную диаграмму растяжения пересчитывают в координатах σ — ε. Ординаты такой диаграммы получают делением растягивающей силы Р на первоначальную площадь поперечного сечения испытуемого образца:

s = Р/F₀.

Абсциссы диаграммы напряжений получают делением абсолютных удлинений расчетной части образца на первоначальную ее длину ε = Dl / l₀.

Полученный таким образом график зависимости напряжений от деформаций не учитывает изменения площади поперечного сечения образца, поэтому он называется условной диаграммой напряжений в отличие от истинной диаграммы напряжений, при построении которой силу Р делят на текущую площадь F поперечного сечения.

На рис. 1 приведены условная (сплошная линия) и истинная (штриховая линия) диаграммы напряжений для низкоуглероди­стой стали. На каждой из них можно отметить ряд характерных точек: А, В, С, D, Е, F.

Вначале на участке ОА диаграмма представляет собой на­клонную прямую. В этих пределах напряжения σ растут пропор­ционально деформациям ε, т. е. соблюдается закон Гукаσ = Еε, где Е — модуль упругости при растяжении. Закон Гука справедлив до предела пропорциональности σ_пр

Выше точки А диаграмма искривляется, закон Гука нарушается. Однако вплоть до точки В, соответствующей пределу упругости σ_уп, деформация образца остается упругой и полностью исчезает при снятии нагрузки. Точка В находится вблизи точки А, поэтому их часто считают совпадающими. Если через точку В провести вертикальную линию, то левее этой линии на диаграмме будет зона упругих, а правее — зона упруго-пластических деформаций, так как там наряду с упругими будут иметь место и остаточные пла­стические деформации, не исчезающие при разгрузке.

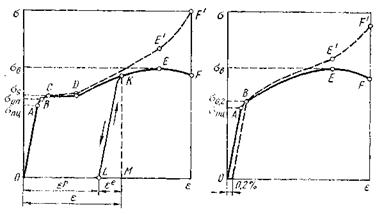
Рис.1 Диаграммы напряжений материала с площадкой текучести (а) и материала без площадки текучести (б)

Начиная от точки С на диаграмме имеется горизонтальный участок, которому соответствует предел текучести σ_s. (σ _т) На этом участке деформации растут без увеличения нагрузки — материал как бы «течет». Поэтому участок CD часто называют площадкой текучести - σ _т.

Наличие площадки текучести для материалов не является характерным. Во многих случаях при испытаниях на растяжение площадка CD не обнаруживается и диаграмма растяжения имеет вид кривых, показанных на рис.1 б. В этом случае предел текучести σ_s определяют условно как напряжение, при котором остаточная деформация составляет заданную величину.

Как показано на рис. 1 а начиная с точки D материал вновь приобретает способность увеличивать сопротивление дальнейшей деформации. Однако возрастание нагрузки при удлинении образца происходит гораздо медленнее, чем на упругом участке. Диаграмма изменяется по плавной кривой с наивысшей точкой Е, в которой условное напряжение (σ = Р/ F ₀) принимает наибольшее значение, достигая временного сопротивления σ_в.

После достижения точки Е на образце намечается место будущего разрыва и образуется шейка — локальное сужение образца. На диаграмме условные напряжения падают, что связано с уменьшением поперечного сечения образца. Однако если подсчитать истинное напряжение, отнесенное к наименьшей площади сечения шейки, то обнаружится возрастание напряжений до момента разрушения (точка F').

РАЗГРУЗКА И ПОВТОРНОЕ НАГРУЖЕНИЕ. Дойдя до некоторой точки К на условной диаграмме напряжений, будем уменьшать нагрузку на испытуемый образец. В процессе разгрузки зависимость σ—ε изобразится прямой KL, параллельной прямой ОА. При разгрузке в области упруго-пластических деформаций деформация полностью не исчезает. Она уменьшается на величину упругой части (отрезок LM). Отрезок OL представляет собой остаточную или пластическую деформацию.

При повторном нагружении образца диаграмма растяжения принимает вид прямой LК и далее — кривой KEF так, как будто промежуточной разгрузки мы не проводили. Таким образом, металл вследствие первоначальной деформации как бы приобретает упругие свойства и повышает предел упругости, одновременно с этим теряя в значительной степени способность к пластической деформации. Это явление называется упрочнением (наклепом).

Аналогичный характер имеют диаграммы напряжений, построенные при сжатии и кручении цилиндрических образцов.

Дата добавления: 2015-06-30