Оценка устойчивости модели

Определение объема выборки (числа прогонов)

Выше было сказано о необходимости проведения нескольких прогонов имитационной модели. Возникает вопрос - сколько про­гонов нужно провести, чтобы сформировать выборочную сово­купность значений определенного параметра, по которой можно найти доверительный интервал?

Точность суждений о значении какого-либо показателя от­клика (например, средней длины очереди) зависит от количества выборочных значений: чем выборка больше, тем точнее результа­ты. Если точность (т.е. доверительный интервал) задается заранее и исследователь остановился на каком-то одном уровне вероятно­сти суждения (чаще Р берется равным 0,95), необходимое количе­ство прогонов (N) определяется путем обратной задачи следую­щим образом:

, (4)

где N₀ - число пробных прогонов; d₀ - длина получившегося по результатам пробных прогонов доверительного интервала (в единицах измерения оцениваемого показателя); d - экспертно определяемая необходимая для исследователя длина доверительного интервала (в единицах измерения оцени­ваемого показателя).

Проведем десять прогонов (N = 10) модели, изменяя границы интервалов поступления автомобилей, но при неизменном сере­динном значении интервала, равного 5 мин:

Значение операнда В блока GENERATE	1,5	1,7	1,8	1,9	2,0	2,5	2,7	2,8	2,9	3,0
Отклик (результат про­гона - средняя длина очереди на заправку, ед.)	3,354	2,555	3,077	3,637	3,392	6,429	6,448	2,330	2,254	4,247

По результатам прогонов:

1) 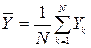=3,772.

2) 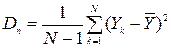= =2,347.

3) по таблице t -Стъюдента при (v = 9) = 2,15

4)доверительный интервал

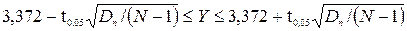или

Таким образом, по результатам пробных прогонов средняя длина очереди с вероятностью 0,95 находится в интервале от 2,86 до 3,88.

Примем, что это для нас недостаточно конкретное значение и
сузим интервал до следующих значений: [3,06; 3,68]. Тогда согласно формуле находим = = 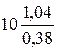27 прогонов.

Под устойчивостью результатов имитации понимается степень нечувствительности ее к изменению входных условий. Ус­тойчивость модели - это ее способность сохранять адекватность на всем диапазоне рабочей нагрузки, а также при внесении изменений в конфигурацию системы. Например, при увеличении работы сис­темы с пяти до восьми часов будет ли разработанная модель с дос­таточной точностью отражать работу системы? Чем ближе струк­тура модели соответствует структуре системы и выше степень ее детализации, тем выше устойчивость модели.

В целом устойчивость результатов моделирования можно оценить дисперсией значений отклика (одного из показателей ра­боты системы, например, коэффициента загрузки устройства). Если при увеличении времени моделирования дисперсия отклика не увеличивается, то результаты работы данной модели устойчивы.

Для получения первой выборочной статистической совокуп­ности, устанавливается какое-либо модельное время, например, пять часов. Затем выбирается некий шаг для контроля величины параметра работы системы, допустим, каждые 30 мин. Выбороч­ная совокупность будет состоять из десяти значений. Проводится расчет дисперсии (D₁). Затем модельное время увеличивается, на­пример, с пяти до восьми часов, и снова осуществляется прогон модели. Новая выборочная совокупность содержит уже 16 значе­ний. Рассчитывается новая дисперсия (D₂). Затем все рассчитан­ные дисперсии сравниваются между собой.

Чтобы результаты моделирования были устойчивыми, дис­персии должны различаться несущественно. Рост разброса кон­тролируемого параметра от начального значения при изменении числа шагов указывает на неустойчивый характер имитации ис­следуемого процесса. Четко установленной методики для проце­дуры проверки устойчивости модели не существует.

Можно установить границы колебания контролируемого па­раметра экспертным путем и если данный параметр выходит за пределы колебаний, то на данном временном интервале констати­руется потеря устойчивости результатов моделирования.

Реже для проверки существенности различия дисперсий ис­пользуется критерий Бартлетта, расчетное значение которого оп­ределяется по формуле:

, (5)

где 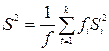, , 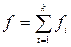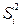- оценки выборочных дисперсий; - объем выборки, если математическое ожидание известно или = n -1 – если неизвестно [2]

Методика проверки статистической гипотезы следующая:

1) Выдвигается нулевая гипотеза Но несущественности расхождений дисперсий значений откликов.

2) По вышеуказанной формуле (5) рассчитывается фактическое значение критерия Бартлетта (B _факт).

3) Определяется теоретическое (табличное) значение крите­рия Бартлетта (B _табл).

4) Сравниваются В _факт и В _табл. Если фактическое значение превышает табличное, то гипотеза о несущественности расхожде­ний дисперсий значений откликов отвергается и принимается про­тивоположная гипотеза (т.е. характер имитации неустойчив), если наоборот - нулевая гипотеза принимается.

Для оценки устойчивости модели может быть также исполь­зован статистический критерий Вилкоксона.

Выберем шаг, по которому будем формировать статисти­ческую совокупность значений длины очереди на заправку, равным
30 мин. Проведем прогон модели со временем 3 часа (180 мин)
(рис. 8).

Рис. 8. Графические результаты прогона модели (модельное время 180 мин)

Зафиксируем длину очереди через каждые 30мин.: 0; 0,5; 1,2; 1,2; 2,5; 1,2. Дисперсия по этим точкам равна 0,71.

Далее проведем прогон модели с модельным временем 300 мин (рис. 9).

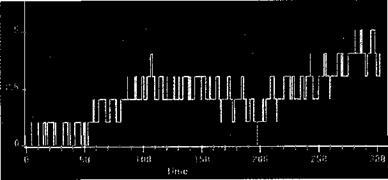
Рис. 9. Графические результаты прогона модели (модельное время 300 мин)

Зафиксируем длину очереди через каждые 30мин.: 0; 0,5; 1,2; 1,2; 2,5; 1,2; 3; 4; 2,3; 5. Дисперсия по этим точкам равна 2,49.

Проведя экспертную оценку существенности различий дис­персий, мы видим, что они сильно (в 3,5 раза) различаются между собой. Поэтому можно констатировать, что при увеличении пе­риода моделирования с трех до пяти часов модель теряет устой­чивость.

Дата добавления: 2015-06-30