Краткая теория. Гармоническим крутильным колебанием тела называется периодическое движение относительно оси, проходящей через центр тяжести этого тела

ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ТЕОРЕМЫ ШТЕЙНЕРА

Гармоническим крутильным колебанием тела называется периодическое движение относительно оси, проходящей через центр тяжести этого тела, когда угол отклонения от положения равновесия изменяется по закону синуса или косинуса.

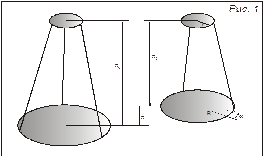Моменты инерции различных тел могут быть измерены методом крутильных колебаний с помощью трифилярного подвеса. Трифилярный подвес представляет собой диск массой m и радиуса R, подвешенный на трех симметрично располо­женных металлических нитях длиной λ., наверху эти нити закреплены по краям диска меньшего радиуса r (рис. 1).

При повороте, верхнего диска на небольшой угол вокруг вертикальной оси, перпендикулярной к плоскости диска и проходящей через его центр, все три нити, вследствие инерционности нижнего диска, примут наклонное положение, центр тяжести системы несколько приподнимется по оси вращения. Нижний диск начнет совершать крутильные колебания, период которых будет зависеть от момента инерции системы

Пусть при вращении диск поднялся на максимальную высоту h = h₁ – h₂, тогда приращение потенциальной энергии составит Δ Π = тgh. При похождении диском положения равновесия, вся его потенциальная энергия переходит в кинетическую: 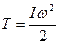. Пренебрегая трением, можно записать закон сохранения механической энергии для этой системы: 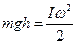(1)

Если угол отклонения невелик, то можно утверждать, что колебания маятника будут происходить по гармоническому закону:

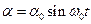(2)

где 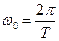– собственная частота колебания системы.

Угловую скорость диска можно найти, продифференцировав уравнение движения .Из уравнения видно, что максимальное значение угловой скорости равно: 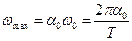(3)

Найдем величину h при повороте диска на малый угол α₀:

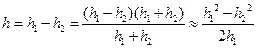(4)

Вследствие малости величины h можно утверждать, что .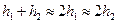

Из рис.1 видно, что по теореме Пифагора 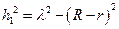, а по теореме косинусов: 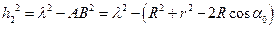. Подставляя значения h₁² и h₂² в (4), получим 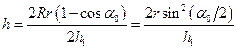. Вследствие малости угла поворота α₀ можно заменить синус угла его аргументом, выраженным в радианах: 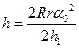. (5)

Выражаем из (1) момент инерции и подставляем значения из (3) и (5):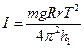

Дата добавления: 2015-06-30