Гладкие частотные фильтры /24/

В некоторых случаях (при последовательном соединении фильтров, при выделении сигналов на уровне сильных помех и т.п.) осцилляции на передаточных характеристиках фильтров являются весьма нежелательными даже при их малой остаточной величине. Так, например, двойное последовательное применение фильтров приводит к тому, что ошибки в полосе пропускания приблизительно удваиваются, а полосе подавления возводятся в квадрат, при этом длина окна эквивалентного фильтра практически удваивается.

Принцип синтеза фильтров. Очевидно, что фильтры с гладкой передаточной характеристикой можно получить только в том случае, если возможно разложение передаточной функции в конечный ряд Фурье.

Допустим, мы имеем симметричный НЦФ с передаточной функцией:

H(w) = h_о+2 h_n cos nw. (7.4.1)

Как известно, cos nw равен полиному по cos w степени n, при этом выражение (7.4.1) можно записать в виде:

H(w) = g_n (cos w)ⁿ = g_n xⁿ, (7.4.2)

где переменная х=cos w изменяется от 1 до -1 (поскольку w изменяется от 0 до p). Преобразование переменной представляет собой нелинейное растяжение оси абсцисс с поворотом на 180^o (по переменной х передаточные функции ФНЧ похожи на ФВЧ, и наоборот) с выражением функции через степенной полином. Последнее примечательно тем, что синтез гладких функций на базе степенных полиномов затруднений не представляет.

Так, например, для конструирования ФНЧ в качестве исходной может быть принята степенная функция вида:

g(x)= (1+x)^z (1-x)^r, (7.4.3)

где z и r - параметры.

Рис. 7.4.1. Примеры синтеза гладких фильтров.

Функция (7.4.3) имеет нули порядка z и r в точках соответственно х = -1 и х = 1 (рис. 7.4.1), при этом значения параметров z и r характеризуют степень касания функцией оси абсцисс. Чем больше порядок, тем медленнее функция отходит ("отрывается") от оси абсцисс.

Если выражение функции (7.4.3) проинтегрировать в пределах от -1 до х и нормировать на значение интеграла от -1 до 1, то будет получена гладкая передаточная характеристика низкочастотного фильтра. На рисунке 7.4.1 приведены передаточные функции для двух пар параметров z и r, вычисленные по формуле:

H(x)= 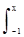g(x)dx / 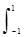g(x)dx. (7.4.4)

Рис. 7.4.2. Схема возврата к ряду Фурье.

Функция H(x) имеет перегиб в точке (z-r)/(z+r) и переходную зону, крутизна которой тем больше, чем больше значения z и r. Подстановкой x=cos w осуществляется возврат к частотной переменной w с сохранением монотонности функции.

В заключение, для определения коэффициентов фильтра h_n требуется осуществить обратное преобразование от степенной формы (7.4.2) к ряду Фурье (7.4.1). Выполнение данной операции достаточно просто производится рекурсивным способом, показанным на рис. 7.4.2. Подробное обоснование рекурсии приведено в /24/.

Дата добавления: 2015-07-02