Дифференцирующие цифровые фильтры

Пример расчета гладкого фильтра.

Произвести расчет ФНЧ с гладкой частотной характеристикой с перегибом характеристики в точке p/3. За исходную функцию принять функцию (7.4.3).

1. x= cos(p/3)= 0.5= (z-r)/(z+r). Принято: z=3, r=1.

Исходный многочлен: g(x) = (1-x)(1+x)³ = 1+2x-2x³-x⁴.

2. H(x)= g(x)dx = C+x+x²-0.5 x⁴-0.2 x⁵. При х= -1, H(-1)= 0, откуда С=0.3. При х=1, H(1)=1.6.

Отсюда: H(x)= (3+10x+10x²-5x⁴-2x⁵)/16. g_n = {3/16, 10/16, 10/16, 0, -5/16, -2/16}.

3. Применяя рекурсивное преобразование, получаем: h_n= {(98, 70, 20, -5, -5, -1)/256}.

Для расчетов гладких фильтров высоких частот в выражении (7.4.4) достаточно поменять местами пределы интегрирования. Гладкие полосовые фильтры получаются комбинацией ФНЧ и ФВЧ с перекрытием частот пропускания.

Курсовая работа 9-07. Разработка методики и программы расчета весовых функций на базе гладких нерекурсивных фильтров.

Передаточная функция. Из выражения для производной d(exp(jwt))/dt = jw exp(jwt)

следует, что при расчете фильтра производной массива данных необходимо аппроксимировать рядом Фурье передаточную функцию вида H(w) = jw. Поскольку коэффициенты такого фильтра будут обладать нечетной симметрией (h_-n = -h_n) и выполняется равенство

h_n [exp(jwn)-exp(-jwn)] = 2j h_n sin nw,

то передаточная характеристика фильтра имеет вид:

H(w) = 2j(h₁ sin w + h₂ sin 2w +... + h_N sin Nw),

т.е. является мнимой нечетной, a сам фильтр является линейной комбинацией разностей симметрично расположенных относительно s_k значений функции. Уравнение фильтрации:

y_n = h_n(s_k+n - s_k-n).

Если дифференцированию подлежит низкочастотный сигнал, а высокие частоты в массиве данных представлены помехами, то для аппроксимации в пределах главного частотного диапазона задается (без индекса мнимости) передаточная функция фильтра вида:

H(w) = w, w £ w_в, H(w) = 0, w_в< w £ w_N.

Оператор дифференцирующего фильтра:

h(n) = (2/p) H(w) sin(npw/w_N) dw, n = 0,1,2,... (7.5.1)

Принимая, как обычно, w_N = p (Dt = 1) и решая (7.5.1) при H(w) = w, получаем:

h_n = (2/p)[sin(nw_в)/n² - w_в cos(nw_в)/n], (7.5.2)

h_о = 0, h_-n = -h_n.

Частотная характеристика:

Im(H(w)) = h_n sin nw = 2 h_n sin nw. (7.5.3)

Точность дифференцирования. На рис. 7.5.1 приведен пример расчета коэффициентов дифференцирующего фильтра на интервал частот {0-0.5}p при Dt=1 (w_в = p/2). Операторы дифференцирующих фильтров, как правило, затухают очень медленно и, соответственно, достаточно точная реализация функции (7.5.3) весьма затруднительна.

Рис. 7.5.1. Коэффициенты оператора фильтра.

Ряд (7.5.3) усекается до N членов, и с помощью весовых функций производится нейтрализация явления Гиббса. Явление Гиббса для дифференцирующих фильтров имеет весьма существенное значение, и может приводить к большим погрешностям при обработке информации, если не произвести его нейтрализацию. Примеры ограничения оператора, приведенного на рис. 7.5.1, и соответствующие передаточные функции H'(w) усеченных операторов показаны на рис. 7.5.2.

Для оценки возможных погрешностей дифференцирования усеченными операторами произведем расчет фильтра при w_в = p/2. По формулам (7.5.2) определяем:

h_0-10 = 0, 0.3183, 0.25, -0.0354, -0.125, 0.0127, 0.0833, -0.0065, -0.0625, 0.0039, 0.05.

Рис. 7.5.2. Частотные функции фильтров.

Произведем проверку работы фильтра на простом массиве данных s_n = n, производная которого постоянна и равна 1. Для массива с постоянной производной фильтр может быть проверен в любой точке массива, в том числе и в точке n=0, для которой имеем:

у = h_n s_o-n = 2 n h_n,

при этом получаем: у=0.5512 при N=5, у=1.53 при N=10.

Рис. 7.5.3. Погрешность дифференцирования.

Такое существенное расхождение с действительным значением производной объясняется тем, что при w=0 тангенс угла наклона реальных передаточных функций фильтра, как это видно на рисунке 7.5.2, весьма существенно отличается от тангенса угла наклона аппроксимируемой функции H(w) = w. На рис. 7.5.3 приведены частотные графики относительной погрешности дифференцирования s = H_н'(w)/H_н(w) с вычислением значений на нулевой частоте по пределам функций при N → ∞. На рис. 7.5.4 приведен пример операции дифференцирования гармоники s с частотой w_o оператором с N=10 в сопоставлении с точным дифференцированием ds/dk.

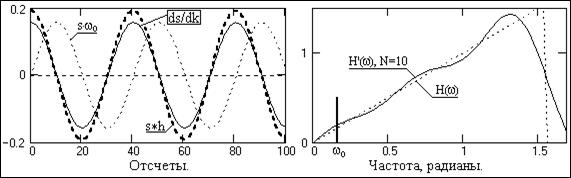
Рис. 7.5.4. Пример операции дифференцирования.

Применение весовых функций. Применим для нейтрализации явления Гиббса весовую функцию Хемминга. Результат нейтрализации для фильтра с N=10 приведен на рис. 7.5.5. Повторим проверочный расчет дифференцирования на массиве s_n = n и получим результат у=1.041, т.е. погрешность дифференцирования уменьшается порядок.

Рис. 7.5.5. Дифференцирование с применением весовой функции.

Аналогично производится расчет и полосовых дифференцирующих фильтров с соответствующим изменением пределов интегрирования в (7.5.1) от w_н до w_в. При этом получаем:

h_n = (w_нcos nw_н-w_вcos nw_в)/(np) + (sin nw_в-sin nw_н)/(n2p).

Фильтры с линейной групповой задержкой. Дифференцирующие фильтры, а равно и любые другие фильтр с мнимой частотной характеристикой, например, оператор преобразования Гильберта, могут быть выполнены в каузальном варианте при условии обеспечения линейной групповой задержки сигнала, которое записывается следующим образом:

j(w) = b - aw, (7.5.4)

где b и a - константы.

Оно выполняется, если импульсная характеристика фильтра имеет положительную симметрию:

h(n) = -h(N-n-1), n = 0, 1, 2, …, (N-1)/2, N – нечетное (тип 1);

n = 0, 1, 2, …, (N/2)-1, N – четное (тип 2).

При этом фазовая характеристика будет определяться длиной фильтра:

a = (N-1)/2, b = p/2.

Частотная характеристика фильтра:

H(w) = |H(w)| exp(jj(w)), (7.5.4)

где модуль |H(w)| задается нечетным. Оба типа фильтров вводят в выходной сигнал сдвиг фазы на 90^о. Кроме того, частотная характеристика фильтра типа 1 всегда равно нулю на частоте Найквиста, что определяется знакопеременностью левой и правой части главного диапазона спектра с учетом периодизации спектра дискретных функций.

Курсовая работа 10-07. Разработать и исследовать оптимальный способ закругления частотной характеристики дифференциального фильтра и реализовать его в программе расчета фильтра и фильтрации цифровых данных..

Дата добавления: 2015-07-02