Уравнивание сети трилатерации параметрическим методом

Студенту предлагается уравнять четырехугольник трилатерации параметрическим способом. Данные представлены в приложении 3. Последовательность уравнительных вычислений проследим на примере сети, изображенной на рис. 3.1.

Рис.3.1. Схема сети трилатерации

Таблица 24

Исходные данные
Пункт	X ( м)	Y (м)
	6013456,321	2373202,505
	6013610,202	2375303,311

Таблица 25

Значения измеренных сторон, приведенных

к центрам знаков и редуцированных на плоскость

Сторона	Длины сторон, (м)
1 – 3	3026,181
1 – 4	2747,965
2 – 3	2389,343
2 – 4	4264,458
2 – 5	2019,859
3 – 4	3343,757
3 – 5	2836,926

Стороны в данной сети приведены к центрам знаков и редуцированы на плоскость в проекции Гаусса-Крюгера, последовательность предварительной обработки измерений описана в предыдущих параграфах. Координаты исходных пунктов представлены в таблице 24, измеренные величины в таблице 25.

В сети измеренными величинами являются длины (n =7), в качестве независимых параметров выберем координаты пунктов 3,4 и 5 (k =6). Далее вычислительный процесс можно разбить на этапы.

1. Согласно алгоритму способа составляем 7 уравнений связи измеренные длины функционально связаны с параметрами (координатами) формулами обратной геодезической задачи:

,

,

,

,

,

,

.

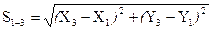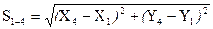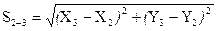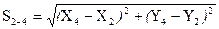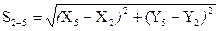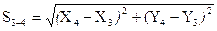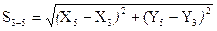2. Определяем веса измеренных величин по формуле , где С =100, принимается условно, чтобы значения весов были близкими к единице, поскольку длины в сети трилатерации измерены светодальномером СТ-5, для вычисления средней квадратической ошибки измерения используем уравнение светодальномера:

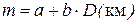, коэффициенты a = 10 мм и b = 5 мм соответствуют светодальномеру СТ-5, D – расстояние в километрах.

Дата добавления: 2015-07-02