Определение активности компонентов расплава

Для термодинамического описания процессов, происходящих при получении стали, необходимо располагать данными по активностям компонентов раствора.

В общем случае под активностью a_i понимают отношение парциального давления пара компонента над раствором 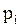к аналогичной величине для стандартного состояния компонента 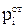[5]:

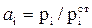. (29)

В стандартном состоянии активность компонента равна 1.

Растворы Fe–R (где R – S, P, O, N, C) при концентрациях, характерных для сталеплавильных процессов, являются разбавленными. В этих случаях за стандартное состояние удобно принять однопроцентный идеальный разбавленный раствор компонента в растворителе 1. Выражение для активности принимает следующий вид:

,

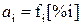где 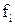– коэффициент активности, характеризующий отклонение от закона Генри;

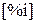– концентрация компонента в %.

Коэффициент активности компонента в растворе, состоящем из компонентов, можно определить по соотношению, предложенному Вагнером:

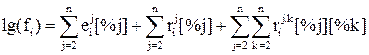, (30)

где 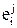– параметр взаимодействия первого порядка;

– параметр взаимодействия второго порядка;

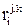– перекрестный параметр взаимодействия.

Параметры взаимодействия определяются по экспериментальным данным соответствующей математической обработкой. Наиболее часто ограничиваются параметрами первого порядка, данные по которым наиболее представительны (табл. 7). В этом случае активность выражается достаточно просто:

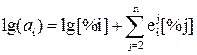. (31)

Таблица 5

Параметры взаимодействия 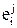в растворах на основе железа (1600 °С)

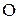
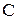
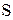
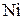
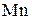
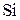
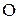
	–0,2	–0,45	–0,133	–0,04	0,006	–0,021	–0,131	0,07
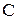
	–0,34	0,14	0,046	–0,024	0,012	–0,012	0,08	0,051
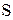
	–0,27	0,11	–0,028	–0,011		–0,026	0,063	0,29

Пример 1. Рассчитать активность серы в расплаве следующего состава, %:

Решение: ;

;

;

.

Пример 2. Проанализировать влияние углерода на активность серы. Концентрация углерода в расплаве изменяется от 0,5 до 2,5%.

Решение. Выделим слагаемое, характеризующее влияние углерода, и представим активность серы в виде

,

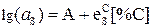где .

В случае расплава из примера 1 величина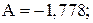

Результаты расчета приведены в табл. 8.

Таблица 8

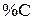
	0,5	0,75	1,00	1,25	1,50	1,75	2,00	2,25	2,50
	1,89	2,02	2,15	2,29	2,44	2,60	2,77	2,95	3,14

Таким образом, увеличение концентрации углерода в расплаве приводит к увеличению активности серы.

Пример 3. Методом ЭДС в легированном расплаве, содержащим 10% 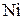, 18% , 0,5% 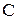и в расплаве, содержащим 0,5% 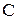определено значение ЭДС=270 мВ, соответствующее 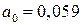. Рассчитать концентрацию кислорода в расплаве заданного состава, а также в расплаве, не содержащем легирующих.

Решение. Выраженная через концентрацию компонентов расплава и параметры взаимодействия первого порядка активность кислорода имеет вид:

.

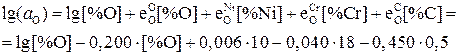Для .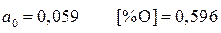

В случае расплава с 0,5% 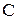концентрация кислорода равна .

Пример 4. Для процесса обезуглероживания, который описывается реакцией

, (32)

определить концентрацию кислорода, соответствующую равновесию с в железе. Расчёт провести для давления 1 атм и 0,1 атм.

Решение. Константа равновесия реакции (32) запишется в виде

.

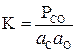Учитывая соотношение между изменением энергии Гиббса и константой равновесия, имеем

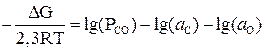. (33)

Выразив активности углерода и кислорода через их концентрации, можем записать

.

Температурная зависимость изменения энергии Гиббса для реакции (32) с учётом того, что для кислорода и углерода за стандартное число принято состояние 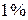-ного раствора, имеет вид

.

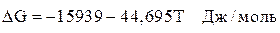Решая уравнение (33) для температуры 1773 К, получаем следующие концентрации кислорода: для давления 1 атм – 0,0032%; 0,1 атм – 0,0003%.

Задание

1. Определить коэффициент активности и активность компонента в расплаве заданного состава (табл. 9).

2. Построить и проанализировать график зависимости .

3. Рассчитать концентрацию кислорода при заданной активности в расплаве, содержащем .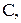

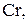
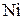4. Определить концентрацию кислорода для процесса обезуглероживания (32), соответствующую равновесию с указанным содержанием углерода в расплаве, содержащем 10% , при давлении

Таблица 9

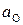
№ вар	Содержание элементов, %				р, атм
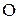
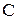
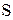
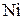
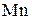
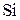
	0,15	0,10	0,05	0,30	0,30	0,35	0,12	0,04		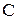	0,02	2,0
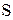
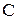
	0,10	0,12	0,05	0,30	0,30	0,30	0,25	0,04			0,03	1,0
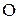
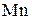
	0,20	0,16	0,05	0,25	0,30	0,45	0,07	0,04			0,04	0,5
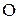
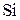
	0,15	0,18	0,05	0,27	0,30	0,50	0,15	0,04			0,05	0,1
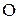
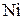
	0,15	0,16	0,05	0,27	0,25	0,40	0,25	0,04			0,06	0,01
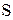
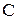
	0,13	0,15	0,05	0,30	0,20	0,90	0,15	0,04			0,07	2,0
	0,13	0,25	0,05	0,25	0,30	0,70	0,07	0,04		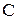	0,06	1,0
	0,12	0,27	0,05	0,20	0,15	0,65	0,09	0,04			0,05	0,5
	0,13	0,32	0,05	0,25	0,30	0,55	0,09	0,04			0,04	0,1
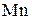
	0,15	0,35	0,04	0,25	0,25	0,65	0,20	0,35			0,03	0,01
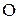
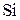
	0,16	0,39	0,04	0,25	0,25	0,70	0,25	0,35			0,02	2,0
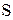
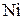
	0,15	0,59	0,04	0,15	0,26	0,20	0,15	0,35			0,03	1,0
	0,20	0,11	0,04	0,30	0,30	0,55	0,22	0,04		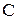	0,04	0,5
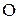
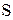
	0,10	0,12	0,04	0,10	0,20	0,95	0,27	0,11			0,05	0,01
	0,20	0,12	0,04	0,30	0,30	1,60	0,25	0,035			0,06	2,0
	0,15	0,14	0,04	0,30	0,30	0,90	0,60	0,035			0,07	1,0
	0,10	0,28	0,035	0,95	0,30	0,65	0,22	0,035			0,06	0,5
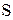
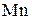
	0,15	0,39	0,035	1,45	0,30	0,47	1,35	0,035			0,05	0,01
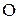
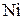
	0,20	0,38	0,035	0,55	1,25	0,72	0,22	0,035			0,04	2,0
	0,15	0,12	0,025	0,75	2,95	0,35	0,28	0,025			0,03	1,0
	0,15	0,21	0,025	0,70	2,85	0,45	0,25	0,025			0,02	0,5
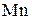
	0,20	0,35	0,025	9,50	0,60	0,80	2,50	0,030			0,03	0,1
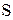
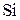
	0,15	0,08	0,025	13,0	0,60	0,80	0,80	0,030			0,04	0,01
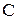
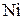
	0,20	0,15	0,025	29,0	0,60	0,80	1,00	0,035			0,05	2,0
	0,20	0,10	0,025	17,5	1,10	1,40	0,60	0,025			0,06	1,0

Контрольные вопросы

1. Понятие термодинамической активности компонентов расплава.

2. Типы стандартных состояний.

3. Термодинамические параметры взаимодействия первого и второго порядка.

4. Связь коэффициентов активности и параметров взаимодействия.

5. Расчет активностей компонентов сложнолегированного металлического расплава.

Дата добавления: 2015-07-02