
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод сечений
|
|
|
|
Частные случаи в методе вырезания узлов
A. Трёхстержневой незагруженный узел, в котором два стержня лежат на одной прямой, а третий расположен под углом (рис. 3.11). Усилия в стержнях, лежащих на одной прямой равнымеждусобой, а усилие в стержне, расположенном под углом, равно нулю.
Докажем это. Рассмотрим, как соотносятся между собой усилия в стержнях,
 |
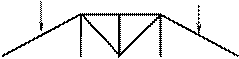
В. Двухстержневой незагруженный узел (рис. 3.12). Усилия в стержнях, соединяющихся в этом узле равно нулю.
| |||||
 | |||||
 |

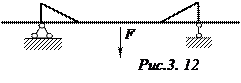 |
Разрежем ферму на две части и отбросим одну из них. Для оставшейся части можно составить три уравнения статического равновесия, куда будут входить внешние нагрузки, опорные реакции и продольные усилия в разрезанных стержнях. Таким образом, если в сечение попадают только три стержня, то при помощи уравнений статики можно определить усилия во всех разрезанных стержнях. Систему трех уравнений по возможности будем сводить к трем разделённым уравнениям, то есть составлять их так, чтобы в них входило 1 неизвестное. Для этого при определении усилия в интересующем нас i - м стержне составляется уравнение: сумма моментов, взятых относительно точки пересечения двух других стержней, попавших в сечение. Эта точка называется моментной точкой для i -го стержня.
На рис. 3.13 показано применение метода сечений при определении усилий в стержнях третьей панели фермы. Для этого проведено сквозное сечение через стержни этой панели (сечение II-II). Усилие в стержне 3-4 найдём из условия равенства нулю суммы моментов сил, приложенных по левую сторону от разреза II—II, относительно точки 8; для определения усилия в стержне 7-8 - относительно точки 3. При определении усилия в стержне 3-8 два стержня, исключаемые из уравнения статики (3-4 и 7-8), параллельны друг другу.
 | |||||
| |||||
|
Найдём усилия в стержнях третьей панели через значения F и d. При этом часть вычислений требуется выполнить самостоятельно.
N3-4=? (сеч.II-II). Искл. N3-8 и N7-8. Моментная точка – 8.
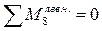 ; VA ∙3d-F/2∙3d-F∙2d-F∙d+N3-4∙h=0; отсюда
; VA ∙3d-F/2∙3d-F∙2d-F∙d+N3-4∙h=0; отсюда

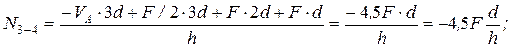 N7-8=? (сеч.II-II). Искл. N3-4 и N3-8. Моментная точка – _____
N7-8=? (сеч.II-II). Искл. N3-4 и N3-8. Моментная точка – _____
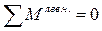 ; ____________________________________ отсюда
; ____________________________________ отсюда


N3-8=? (сеч.II-II). Искл. N3-4 и N7-8.
Моментная точка уходит в бесконечность, т. к. исключаемые стержни параллельны. Поэтому берём сумму проекций всех сил левой части фермы на ось Y.
 ; ___________________________ отсюда
; ___________________________ отсюда

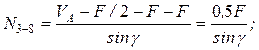
Можно проверить правильность вычисления усилий. Для этого возьмём сумму проекций всех сил левой части фермы на ось X.
 ; N3-4+ N7-8+N3-8 cos γ=
; N3-4+ N7-8+N3-8 cos γ= 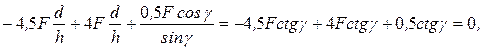 0º0.
0º0.
 | |||
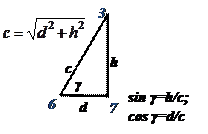 | |||
Другой способ вычисления плеча силы дан в приложении IV.
|
|
|
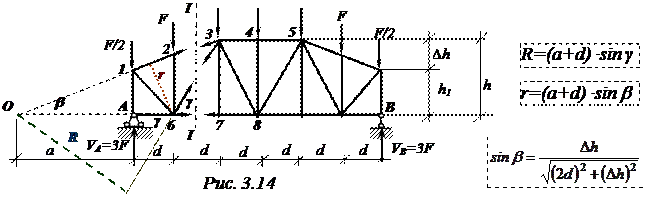 |
N6-7=? (сеч.I-I). Искл. N2-3 и N6-3. Моментная точка - 3.
 ; VA ∙2d-F/2∙2d-F∙d-N6-7∙rh=0; отсюда
; VA ∙2d-F/2∙2d-F∙d-N6-7∙rh=0; отсюда
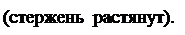
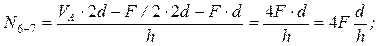
N2-3=? (сеч.I-I). Искл. N6-3 и N6-7.
Моментная точка (точка их пересечения ) _________
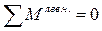 ; ______________________________ отсюда
; ______________________________ отсюда
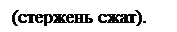

N6-3=? (сеч.I-I). Искл. N2-3 и N6-7. Моментная точка – О.
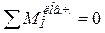 ; - VA ∙a+F/2∙a+F∙(d+a)-N3-6 R=0; отсюда
; - VA ∙a+F/2∙a+F∙(d+a)-N3-6 R=0; отсюда
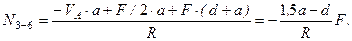
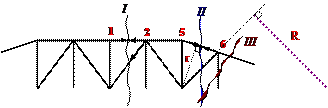
Пример 3.1. Требуется: определить усилия в стержнях 6-й и 8-й панели.
1. Приводим равномерно распределённую нагрузки q=2 кН/м по нижнему поясук узловой. Узловая нагрузка равна q∙d=2∙3=6 кН для средних узлов и q∙d/2=3 кН для крайних.
 | |||
 | |||















 |



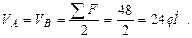 |
2. Определим опорные реакции:
3. Найдём усилий в стержнях 6 и 8 панели, включая стойки этих панелей.
 (сечение I–I). Исключаем N 2-3 и N 3-4.
(сечение I–I). Исключаем N 2-3 и N 3-4. 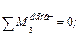


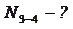 (сечение I–I). Исключаем N 2-3 и N 1-2.
(сечение I–I). Исключаем N 2-3 и N 1-2. 
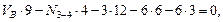


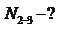
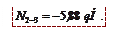 (сечение I–I). Исключаем N 3-4 и N 1-2.
(сечение I–I). Исключаем N 3-4 и N 1-2.

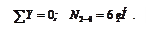
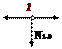
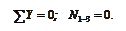
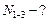 (вырезаем узел 1)
(вырезаем узел 1)

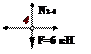

 (сечение II–II). Исключаем N 6-7 и N 7-8.
(сечение II–II). Исключаем N 6-7 и N 7-8. 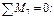


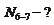 (сечение II–II). Исключаем N 5-6 и N 7-8.
(сечение II–II). Исключаем N 5-6 и N 7-8. 
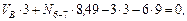

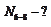
(сечение III-III) Исключаем N 6-9 и N 7-8. 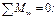


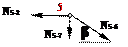
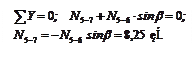


|

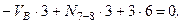

Вопросы и задачи для закрепления темы
1. Чем отличается реальная конструкция фермы от её расчетной схемы? Почему нагрузку в ферме приводят к узловой?
2. Записать условие статической определимости и статической неопределимости фермы. Доказать статическую определимость фермы пункта 5.
3. Cформулировать общий принцип подбора уравнений статики при определении усилия в стержне методом сечений.
4. Показать часть фермы, отсечённую сечением, сделанным для определения усилия в стержнях 4-5. Записать уравнение статики, из которого определяется это усилие в общем и развёрнутом виде.
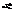


5. Перечислить нулевые стержни в ферме
   |
6. - 8. Определить усилия в указанных
стержнях
  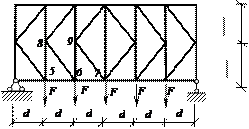 |
9. 10. Определить усилия в указанных стержнях
полураскосной фермы.
|
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 1226; Нарушение авторских прав?; Мы поможем в написании вашей работы!
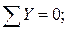 Ni∙sinα =0; Ni=0.
Ni∙sinα =0; Ni=0.
 ; Ni cosα +Nj =0; отсюда Nj∙=0.
; Ni cosα +Nj =0; отсюда Nj∙=0.
