Общие сведения

КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

Годовые пробеги АТС млн.км.

Исходные данные.

Учебно - тематический план

№	Наименование темы.	Количество часов.
всего	теория	практика
1.	Вводное занятие. История развития творчества			-
2.	Оборудования, материалы, инструменты. Организация рабочего места. Правила техники безопасности.
3.	Тренировочные упражнения по вырезанию линий различной сложности (прямая, полукруг, овал, зигзаг и пр.) Техника безотрывного вырезания.
4.	Понятие о трёх видах вырезания: Силуэт, Прорезь, Ажурная прорезу.			-
5.	Практическая работа. Вырезание простых силуэтов.
6.	Виды бумаги. Цвет. Особенности использования цвета при составлении работ...
7.	Совмещение работы и фона.
8.	Раскрашивание силуэтов.
9.	Упражнения на прорезь. Простейшая прорезь с элементами аппликации (практическая работа)		-
10.	Прорезь силуэтов		-
11.	Ажурная прорезь		-
12.	Оформление работ. Рамка. Разновидности рамок
13.	Выставки: «Мои первые работы»-ноябрь Тематическая-март Итоговая-май
14.	Внеклассные занятия (плетение, оригами)		-
15.	Участие в празднике народных мастеров			-
16.	Итоговое занятие.		-
	Итого:

Л/а	Груз/бенз.	Груз/диз.	Авт/бенз.	Авт/диз.
По территории города
660,1	589,07	76,61	253,3	25,1

Для легковых автомобилей k-го класса с двигателем g-го типа:

M ikg = m jkg *L kg *K rig *K tig; т.

%	Рабочий объем двигателя, л.	Населенный пункт
СО	СН	NOx
	<1,3	11,4	2,1	1,3
	1,3-1,8		2,6	1,5
	1,8-3,5		2,8	2,7

Для грузовых автомобилей k-го класса с двигателем g-го типа:

M ikg = m jkg* L kg *K nig *K rig *K tig; т.

%	Грузоподъемность, т.	Тип двигателя	Населенный пункт
СО	СН	NOx
	0,5-2,0	Б		3,4	2,6
	2,0-5,0	Б	52,6	4,7	5,1
	2,0-5,0	Д	2,8	1,1	8,2
	5,0-8,0	Б	73,2	5,5	9,2
	5,0-8,0	Д	3,2	1,3	11,4
	8,0-16,0	Б	97,8	8,2
	8,0-16,0	Д	3,9	1,6	13,4
	>16.0	Д	4,5	1,8	16,4

Для автомобилей k-го класса с двигателем g-го типа, использующихся на перевозках h-го типа: M ikgh = m jkg* L kgh *K nig *K rig *K tig; т.

%	Класс автобуса (l – габаритная длина, м.)	Тип двигателя	Населенный пункт
СО	СН	NOx
	<5.0	Б	13.5	2.9
	6.0-7.5	Б		3.4	6.1
31,5	8.0-9.5	Б	67.1		9.9
	7.5-9.5	Д	4.5	1.4	9.1
	10.5-12.0	Б		7.7	10.4
	10.5-12.0	Д	4.9	1.6
	>12.0	Д		1.6
31,5	8.0-9.5	Б	67.1		9.1

Рассмотрим цепь, содержащую последовательное соединение резистивного (активного) сопротивления R и катушку индуктивностью L.

По второму закону Кирхгофа для мгновенных значений приложенного напряжения 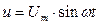к зажимам цепи равно падению напряжения на активном сопротивлении и падению напряжения на индуктивности.

.

(1.1)

Записанное уравнение в комплексной форме для действующих значений

,

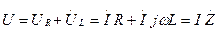(1.2)

где – комплекс полного сопротивления цепи (Ом):

,

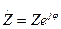(1.3)

где 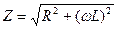- модуль полного сопротивления,

- угол сдвига фаз между синусоидами тока и напряжения (аргумент комплексного сопротивления):

.

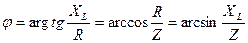(1.4)

Таким образом, напряжение на входе цепи с активно-индуктивной нагрузкой опережает ток на угол φ, т.е. φ > 0. Временная диаграмма и векторная диаграммы напряжений изображены на рис.1.1.

а) б)

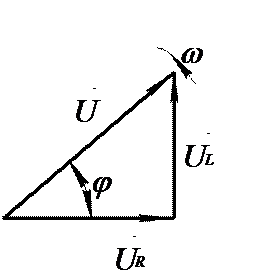
в)

Рис. 1.1. Схема RL - цепи (а), временная диаграмма (б) и векторная диаграммы (в)

Соотношение между векторами 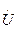, 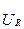и можно представить в виде треугольника напряжений (рис.1.1в).

Порядок построения векторной диаграммы напряжений следующий:

1.Проводим действительную и мнимую оси комплексной плоскости (1, j)

2.Выбираем вектор, c которого начинаем построение. При последовательном соединении сопротивлений построение диаграммы напряжений надо начинать с вектора тока - , он является общим для обоих элементов.

3. Строим вектор напряжения на активном сопротивлении . Он совпадает с вектором тока .

4. Строим вектор напряжения на индуктивном сопротивлении . Этот вектор равен вектору тока , умноженному на . Умножение вектора на величину, содержащую j (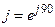), приводит к повороту вектора против часовой стрелки на угол 90^○.

5. Сложив два вектора напряжения, получим согласно (1.2) вектор приложенного напряжения .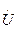

Из треугольника напряжений (рис.1.2а) следует, что вектор приложенного напряжения 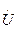состоит из активной и реактивной составляющих напряжения которые определяются по следующим формулам:

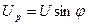,	(1.5)
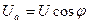.	(1.6)

Если комплексное напряжение на цепи разделить на комплексный ток, то получим комплексное сопротивление:

.

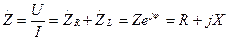(1.7)

Соотношение между векторам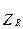и , и 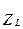можно представить в виде треугольника сопротивлений о’a’ b’ (рис.1.2б), при этом гипотенуза представляет полное сопротивление цепи Z, а два катета - активное R и реактивное X сопротивления цепи.

Из треугольника сопротивлений (рис.1.2б) активная и реактивная составляющие сопротивлений определяются по следующим формулам:

,	(1.8)
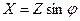.	(1.9)

Если каждую сторону векторного треугольника напряжений 0''а''в'' умножить на вектор тока, получим прямоугольный скалярный треугольник мощностей (Р=U^.I), где в масштабе мощностей гипотенуза представляет полную мощность цепи S, а два катета - активную Р и реактивную Q мощности цепи.

Из треугольника мощностей (рис.1.2в) активная, реактивная и полная мощность определяются по следующим формулам:

,	(1.10)
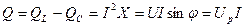,	(1.11)
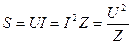
	(1.12)

а) б) в)

Рис. 1.2 Треугольники напряжений (а), сопротивлений (б), мощностей (в)

1.2. ИЗМЕРЕНИЕ ПАРАМЕТРОВ RL – ЦЕПИ С РЕАЛЬНОЙ КАТУШКИ ИНДУКТИВНОСТИ

Практически любая катушка индуктивности обладает не только индуктивностью L, но активным сопротивлением потерь R_k, которое связано с резистивным сопротивлением провода, которая намотана катушка.

Схема RL – цепи с учетом активного сопротивления потерь R_k в катушке приведена на рис.1.3.

Рис. 1.3. Схема RL – цепи с учетом активного сопротивления потерь R_k в катушке индуктивности

Для определения параметров катушки (R_k и L) необходимо c помощью вольтметра измерить U, U_R, U_Lк и построить векторную диаграмму, используя измеренные напряжения U, U_R, U_Lк.

Треугольник напряжений строится методом засечек по известным модулям | 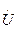|, | | и | 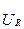| и известной фазе 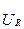относительно .

Порядок построения треугольника напряжений (рис. 1.4):

1. Проводим действительную и мнимую оси комплексной плоскости (1, j)

2. Выбираем вектор, c которого начинаем построение диаграммы. При последовательном соединении сопротивлений построение диаграммы напряжений надо начинать с вектора тока – , он является общим для обоих элементов. Считаем, что он имеет нулевую начальную фазу и потому совпадает с реальной осью 1.

3. Строим вектор напряжения на активном сопротивлении . Он совпадает с вектором тока .

4. Из начала координат 0 строим окружность с радиусом, пропорциональным измеренному напряжению U.

5. Из конца вектора 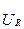(точка а) строим окружность с радиусом, пропорциональным измеренному напряжению U_L.

6. Засекаем, находим, точку пересечения двух окружностей (точка В).

7. Из точки В опускаем перпендикуляр на реальную ось и находим точку б.

Рис. 1.4. Векторная диаграмма напряжений для RL – цепи c реальной катушки индуктивности

Из векторной диаграммы следует:

.

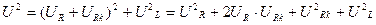(1.13)

Ввиду того, что получим:

.

(1.14)

Отсюда активная и реактивная составляющие напряжения катушки:

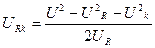,	(1.15)
.	(1.16)

Другие величины могут быть вычислены используя, следующие формулы:

Сопротивление резистора R:

.

(1.17)

Резистивное сопротивление катушки индуктивности R_к:

.

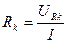(1.18)

Реактивное сопротивление катушки индуктивности X_k:

.

(1.19)

Отсюда индуктивность катушки индуктивности L_k:

.

(1.20)

Модуль комплексного сопротивления катушки индуктивности Z_k:

.

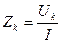(1.21)

Фазовый сдвиг между током и напряжением на катушке индуктивности φ_к:

.

(1.22)

Активная мощность P:

,

(1.23)

где

.

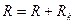(1.24)

Реактивная мощность Q:

.

(1.25)

Полная мощность S:

.

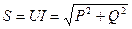(1.26)

Коэффициент мощности cosφ:

.

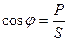(1.27)

1. Что называется переменным током?

2. Что называется периодом переменного тока?

3. В каких единицах измеряется частота переменного тока?

4. В какой цепи переменного тока ток и напряжение совпадают по фазе?

5. От каких величин зависит индуктивное сопротивление катушки?

6. По какой формуле можно вычислить сопротивление цепи переменного тока, содержащей активное и индуктивное сопротивления?

7. От каких величин зависит полная мощность генератора переменного тока?

8. Что называется коэффициентом мощности?

9. Какие методы применяют для определения параметров последовательной и параллельной схем замещения пассив­ного двухполюсника? В чем заключается сущность каждого метода?

10. Как определяют параметры последовательной схемы замещения пассивного двухполюсника методом трех вольт­метров при аналитическом расчете и путем построения век­торных диаграмм? Каким способом устанавливают знак ре­активного сопротивления двухполюсника?

11. Как определяют параметры параллельной схемы заме­щения пассивного двухполюсника методом трех ампермет­ров при аналитическом расчете и путем построения вектор­ных диаграмм? Каким способом устанавливают знак реак­тивной проводимости двухполюсника?

12. Как перейти от параметров последовательной схемы замещения к параметрам параллельной схемы замещения пассивного двухполюсника?

13. Как перейти от параметров параллельной схемы заме­щения к параметрам последовательной схемы замещения пассивного двухполюсника?

14. Как определить параметры последовательной схемы замещения двухполюсника, эквивалентного двум последова­тельно включенным пассивным двухполюсникам, если из­вестны:

а) комплексные сопротивления;

б) комплексные проводимости этих двухполюсников?

15. Как определить параметры параллельной схемы заме­щения двухполюсника, эквивалентного двум параллельно включенным пассивным двухполюсникам, если известны:

а) комплексные проводимости;

б) комплексные сопротивления этих двухполюсников?

16. Что такое коэффициент мощности приемника и как его определяют по известным параметрам последовательной и параллельной схем замещения?

17. С какой целью и каким образом осуществляют ком­пенсацию реактивной мощности активно-индуктивного при­емника?

18. Какие схемы включения конденсатора применяют для компенсации реактивной мощности приемников?

19. Как рассчитать емкость компенсирующего конденса­тора при включении его параллельно активно-индуктивному приемнику, если необходимо повысить коэффициент мощно­сти приемника до требуемого значения ?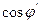

20. Как рассчитать емкость компенсирующего конденса­тора при включении его последовательно с активно-индук­тивным приемником, если необходимо повысить коэффици­ент мощности приемника до требуемого значения ?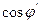

21. Как экспериментально определить ток ветви при от­сутствии амперметра? Какому условию должно удовлетво­рять сопротивление резистора, используемого при измере­ниях?

22. Чему равны комплексное и полное сопротивления по­следовательного соединения:

а) индуктивной катушки и резистора;

б) конденсатора и резистора?

23. В каких пределах может изменяться разность фаз напряжения и тока для последовательного соединения:

а) индуктивной катушки и резистора;

б) конденсатора и резистора?

Приведите векторные диаграммы.

24. Чему равны комплексное и полное сопротивления по­следовательного соединения резистора, индуктивной катуш­ки и конденсатора?

25. В каких пределах может изменяться разность фаз напряжения и тока для последовательного соединения резис­тора, индуктивной катушки и конденсатора? Приведите век­торные диаграммы.

26. Чему равны комплексная и полная проводимости па­раллельного соединения:

а) индуктивной катушки и резистора;

б) конденсатора и резистора?

27. В каких пределах может изменяться разность фаз напряжения и тока для параллельного соединения:

а) индуктивной катушки и резистора;

б) конденсатора и резистора?

Приведите векторные диаграммы.

29. Чему равны комплексная и полная проводимости па­раллельного соединения резистора, индуктивной катушки и конденсатора?

30. В каких пределах может изменяться разность фаз на­пряжения и тока для параллельного соединения резистора, индуктивной катушки и конденсатора? Приведите векторные диаграммы.

31. Какие процессы происходят на активном, индуктивном и емкостном элементах в цепи синусоидального тока?

32. Как определить индуктивное и емкостное сопротивление по заданным значениям L, C и частоты f?

33. Как определить параметры цепи синусоидального тока при наличии амперметра, вольтметра и ваттметра?

34. Как определить параметры цепи синусоидального тока при наличии только амперметра и вольтметра?

35. Каким соотношением определяется полное сопротивление цепи при наличии R, L, C элементов?

36. Как определить активные и реактивные составляющие напряжений, сопротивлений, мощностей, если известные полные значения указанных величин и углы сдвига фаз между синусоидами тока и напряжения?

37. Как сдвинуты относительно друг друга синусоиды (векторы) тока и напряжения на R, L, C элементах в цепи синусоидального тока?

Дата добавления: 2015-07-02