Крышка корпуса

Корпус насоса

Расчет насоса на прочность

Рабочие условия для проектирования:

Давление условное - Р_у = 4 мПа.

Температура - t = 400 ºC.

Среда - нефтепродукт.

Материал – стальное литье марки 25л – II по ГОСТ 977-75 с пределом прочности при растяжении δ_в = 12 МПа.

Толщину стенки корпуса определяем по формуле:

,

где P _y – условное давление, Р _у = 4 МПа;

D – максимальный внутренний диаметр корпуса, D = 0,491 м.;

R_z – допускаемое напряжение.

Исходя из запаса прочности 4,35 получаем R_z = 103,5 МПа.

С – прибавка на коррозию, С = 0,004 м.

Подставляя значение величин, получим толщину стенки:

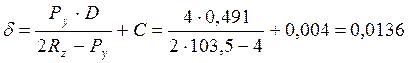м.

Принимаем толщину стенки корпуса: м.

Напряжение в стенке крышки оцениваем, рассматривая ее как кольцевую пластину, внешний край которой заделан по контуру радиуса R ₁ и неподвижен, а внутренний край заделан и может прогибаться. Считаем, что пластина нагружена по всей поверхности равномерно распределенным давлением Р_у = 4 МПа. Принятая расчетная схема приведена на рисунке 2.3.

Максимальное напряжение определяется по формуле:

,

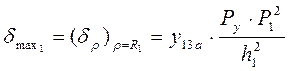где y _13a – коэффициент, зависящий от отношения r₁/R₁;

h ₁ – толщина пластины, h ₁ = 0,025 м.

при ; коэффициент y_13a = 0,53.

Тогд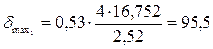а МПа.

При этом на контуре радиуса R₁,будет действовать изгибающий момент интенсивностью:

Н•м/м.

Для оценки напряжения во фланце крышки рассмотрим его как

кольцевую пластину с защемленным внешним и свободным внутренним краем, находящуюся под действием:

1) контурной нагрузкой, суммарно равной Q, возникающей от действия гидростатического давления Р_у = 4 МПа на стенку крышки.

Н

2) контурной нагрузкой, суммарно равной Q₂, возникающей при сжатии двух спирально – навитых прокладок. (Условно удваиваем нагрузку от сжатия прокладки большего диаметра):

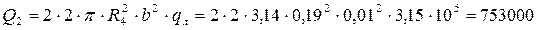Н.

Q₂ = 753000 H,

где b = 0,01 м – ширина прокладки;

q = 31,5 МПа – удельное давление необходимое для сжатия прокладки;

R₄ = 0,19 м – по рисунку 2.2;

3) изгибающего момента интенсивностью

М_ρ=R1 = 995 Н м/м.

Будем считать, что пластина защемлена по контуру расположения шпилек R₂ = 0,22 м.

За внутренний край пластины принимаем контур радиуса R₁ = 0,167 м.

Для упрощения расчета считаем, что контурная нагрузка Q₂ так же как и нагрузка Q ₁ и момент М_ρ=R1 приложены по контуру R ₁. Принятая расчетная схема показана на рисунке 2.3.

Напряжение на внешнем крае пластины:

,

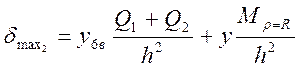при коэффициент y_{6 в} = 0,13 и у =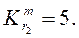

(коэффициент получен линейкой интерполяцией). Подставив значение в приведенную выше формулу, получим:

МПа.

Дата добавления: 2015-07-02