Определение и формулы вычисления центров тяжести

ЦЕНТР ТЯЖЕСТИ

Методические указания к выполнению

расчетно-графической работы

Ростов-на-Дону

УДК 531.01

Центр тяжести: методические указания к выполнению расчетно-графической работы. – Ростов-на-Дону: Рост. гос. строит. ун-т, 2010.-23с.

Предназначены для студентов дневного и заочного отделений всех специальностей при выполнении расчетно-графической работы. Приведены основные способы нахождения центра тяжести, даны решения определения центра тяжести сложных фигур.

УДК 531.01

Составитель: канд.техн.наук, доц. Д.А.Высоковский

Рецензент: канд.физ.-мат.наук Е.Б. Русакова

Редактор Н. Е. Гладких

Темплан 2010г., поз. 192

Подписано в печать 26.04.10. Формат 60х84/16

Бумага писчая. Ризограф. Уч.изд.л. 1,5

Тираж 100 экз. Заказ 545.

Редакционно-издательский центр РГСУ.

344022, Ростов-на-Дону, ул. Социалистическая, 162

© Ростовский государственный

строительный университет, 2010

Рассмотрим произвольное тело. Мысленно разобьем его на достаточно большое число малых по сравнению с телом частей произвольной формы. По закону всемирного тяготения на все части тела, находящегося вблизи земной поверхности, действует силы притяжения этих тел к Земле, т.е. силы тяжести. Силу тяжести i -й малой или элементарной частицы тела обозначим через , а силу тяжести всего тела — через .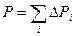

Силы тяжести элементарных частиц направлены к центру Земли, т.е. образуют систему сходящихся сил. Так как расстояние до центра Земли чрезвычайно велико по сравнению с расстояниями между частицами тела, то можно считать силы тяжести элементарных частиц тела системой параллельных сил, направленных в одну сторону.

Как бы мы не поворачивали тело и не изменяли его положение в пространстве, силы тяжести отдельных его частиц останутся параллельными друг другу; относительно тела они будут поворачиваться вокруг своих точек приложения, сохраняя свою параллельность и величину. При таком повороте равнодействующая параллельных сил всегда проходит через одну и ту же точку— центр данной системы параллельных сил. Эта точка называется центром тяжести тела.

Таким образом, центр тяжести тела это такая, неизменно связанная с этим телом, точка, через которую проходит линия действия равнодействующей сил тяжести данного тела при любом положении тела в пространстве.

Центр тяжести — это точка, которая может лежать и вне пределов данного тела. Например, центром тяжести кольца служит его геометрический центр, так как при любом положении кольца через эту точку будет проходить равнодействующая сил тяжести его элементарных частей.

Радиус-вектор центра тяжести тела 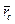вычисляем как радиус-вектор центра параллельных сил (рис.1) по формуле:

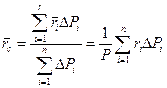, (1)

здесь 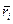— радиус-вектор точки приложения силы тяжести i -й элементарной частицы тела, — сила тяжести i элементарной части, n — число частей, на которое разбито тело. — сила тяжести всего тела.

Рис. 1

Если в формуле (1) перейти к пределу, увеличивая число элементарных частей n до бесконечности, то после замены дифференциалом dP, а суммы — интегралом получим

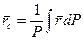. (2)

Здесь 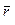— радиус-вектор элементарной части тела, принятой за точку.

Если (1) и (2) спроектировать на декартовые оси координат, то будем иметь:

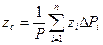; ; ; (3)

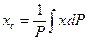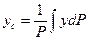; ; , (4)

где x_с , y_c, z_с — координаты центра тяжести; x_i, y_i, z_i — координаты точки приложения силы .

Введем понятие центра масс тела, используя понятие его центра тяжести. Силы тяжести элементарных частиц тела и всего тела можно выразить через их массы и M и ускорение силы тяжести g с помощью формул 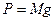, . Подставляем эти выражения сил тяжести (1) и (2) и сокращаем на g, получим:

(5)

и

. (6)

По формулам (5) и (6) вычисляется радиус-вектор центра масс тела. В проекциях на оси координат

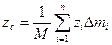; ; ; (7)

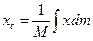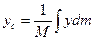; ; ; (8)

здесь x_с , y_c, z_с — координаты центра масс тела.

Для однородного тела сила тяжести и масса всего тела

; ,

где М — объем тела, и - соответственно удельный вес и плотность тела.

Для элементарной части тела

; ,

где — объем элементарной части.

Подставляем эти значения в (1) и (2), получаем формулы:

; ,

по которым определяют центр тяжести объема тела.

В проекциях на координатные оси.

; ; ; (9)

; ; . (10)

В случае однородной плоской фигуры, например тонкого листа железа, имеем

; ,

где F — площадь всей поверхности; — площадь элементарной частички поверхности.

Для однородной плоской фигуры получаем следующие формулы, по которым вычисляют центр тяжести ее площадки:

; ; (11)

; . (12)

Интегралы в формулах (12) называются статическими моментами площади плоской фигуры относительно осей Ох и Оу соответственно

; . (13)

В случае однородной линии, например тел типа проволоки, с постоянной площадью сечения, радиус-вектор центра тяжести длины линии можно определить по формулам:

; .

Здесь 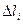— длина элемента линии, l —общая длина линии, центр тяжести которой

; ; (14)

; . (15)

Дата добавления: 2015-07-02