
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Энтропия и избыточность источника сообщений
|
|
|
|
Рассмотрим источник информации, который выдает последовательность независимых дискретных сообщений xi. Каждое сообщение случайным образом выбирается из алфавита источника X = x 1… xn (n – размер алфавита источника). Такой источник информации называется источником без памяти с конечным дискретным алфавитом, а сообщения, вырабатываемые им, называются простыми. В дальнейшем, для упрощения расчетов, будем работать именно с такими источниками.
Количество информации, содержащейся в одном элементарном сообщении источника (см. формулу 7) еще никак его не характеризует, так как одни элементарные сообщения могут нести в себе много информации, но при этом передаваться редко, а другие сообщения могут нести мало информации, но передаваться часто. Поэтому источник может быть охарактеризован средним количеством информации, приходящимся на одно элементарное сообщение – энтропия источника [1, 6, 7]:
 [ бит ], [ бит ],
| (8) |
где X – алфавит сообщений источника информации; n – размер алфавита источника.
Энтропия обладает рядом свойств:
1. Во-первых, Н(Х) ≥ 0. Положительность Н(Х) видна из (8), так как вероятности положительны и заключены между нулем и единицей, логарифмы таких чисел отрицательны, а равенство нулю возможно только для такого случая, когда вероятность появления одного из сообщений источника равна единицы, а для остальных равна нулю.
2. Во-вторых, при заданном размере алфавита источника n энтропия максимальна и равна Н(Х) = log2 n, когда вероятности появления сообщений источника равны, т.е. сообщения равновероятны.
3. В-третьих, энтропия обладает свойством аддитивности:
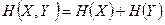 , ,
| (9) |
где Н(Х) – энтропия первого источника информации; Н(Y) – энтропия второго источника информации.
Пример 2. Представим источник сообщений в виде корзины, в которой находятся шары трех цветов: красный, зеленый и синий. Данные шары (сообщения) определяют размер алфавита источника.
Рассчитаем энтропию источника сообщений если:
1) красных шаров – 7 шт., зеленых шаров – 5 шт., синих шаров – 2 шт.
2) красных, зеленых и синих шаров – 2 шт.
Решение: В корзине находятся шары трех цветов, следовательно, размер алфавита источника n = 3.
1) Вероятность появления красного шара р 1 =  ; зеленого шара р 2 =
; зеленого шара р 2 =  ; синего шара р 1 =
; синего шара р 1 = 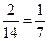 ;
;
Рассчитаем энтропию источника:
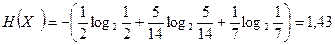 [ бит ] [ бит ]
|
2) Вероятность появления красного шара р 1 = 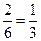 ; зеленого шара р 2 =
; зеленого шара р 2 =  ; синего шара р 1 =
; синего шара р 1 =  ;
;
Рассчитаем энтропию источника:
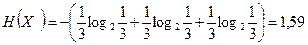 [ бит ] [ бит ]
|
Как видно из вышеизложенного, энтропия определяет среднее число двоичных знаков, необходимых для кодирования исходных символов источника информации. Она максимальна, когда символы вырабатываются источником с равной вероятностью. Если же некоторые символы появляются чаще других, энтропия уменьшается. Чем меньше энтропия источника отличается от максимальной, тем рациональнее он работает, тем большее количество информации несут его символы.
Для сравнения источников по их информативности вводится параметр, называемый избыточностью и равный [1, 6, 7]:
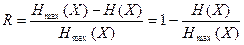 , ,
| (10) |
где Нmax(Х) – максимальная энтропия источника.
Источник, избыточность которого R = 0, называют оптимальным. Все реальные источники имеют избыточность R ≠ 0.
Предположим, что мы получили одинаковое количество информации I 0 от реального и оптимального источников. Тогда число символов k, затраченных на передачу этого количества информации реальным источником, будет больше числа символов kmin затраченных оптимальным источником. Зная число символов k и kmin можно также рассчитать избыточность:
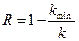
| (11) |
Избыточность увеличивает время передачи информации, поэтому она нежелательна. Однако, при передаче сообщений, при наличии помех в канале связи, избыточность используется для увеличения помехозащищенности передаваемых сообщений (помехоустойчивое кодирование).
Пример 3. Пусть источник информации передает русский текст. Если не различать буквы «е» и «ё», а также мягкий и твердый знаки, то в русском алфавите 31 буква; добавим пробел между словами и получим 32 символа.
Покажем, что пятиразрядный двоичный код (код Боде) не является оптимальным для передачи русского текста.
Решение: В данном коде на представление каждой буквы тратятся пять элементарных символов. Максимальная энтропия источника, использующего для передачи русского алфавита пятизначный код Боде равна Нmах(X) = log 232 = 5 (бит). В данном случае считается, что все буквы русского алфавита имеют одинаковую вероятность и статически независимы.
С учётом различной вероятности появления букв в тексте энтропия равна:
Н(X) = 4,42 [ бит ].
С учётом корреляции между двумя и тремя соседними буквами энтропия равна:
Н(X) = 3,52 [ бит ].
4. С учётом корреляции между восемью и более символами энтропия равна:
Н(X) = 2 [ бит ].
Далее всё остаётся без изменений.
Рассчитаем избыточность представленного источника информации при кодировании символов пятиразрядным двоичным кодом Боде:

Таким образом, можно сделать вывод, что каждые 6 букв из десяти являются избыточными и могут просто не передаваться, т.е. избыточность русского текста составляет 60 %.
Такой же и более высокой избыточностью обладают и другие источники информации – речь, музыка, ТВ изображения и т.д.
Зная энтропию Н(X) и время  , которое занимает в среднем каждое элементарное сообщение, можно рассчитать одну из важнейших характеристик источника – производительность (среднее количество информации в единицу времени) [1, 6, 7]:
, которое занимает в среднем каждое элементарное сообщение, можно рассчитать одну из важнейших характеристик источника – производительность (среднее количество информации в единицу времени) [1, 6, 7]:
 = =  , , 
| (12) |
Время  рассчитывается следующим образом:
рассчитывается следующим образом:
 = = 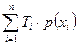 , ,
| (13) |
где  - длительность i -го сообщения; p(xi) – вероятность появления i -го сообщения.
- длительность i -го сообщения; p(xi) – вероятность появления i -го сообщения.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 8092; Нарушение авторских прав?; Мы поможем в написании вашей работы!