Корректирующие коды Хэмминга

Корректирующий код Хэмминга относится к категории неразделимых кодов. Если в разделимых (блочных) кодах все контрольные символы размещаются либо в начале, либо в конце кодовой комбинации, то в коде Хэмминга контрольные разряды располагаются среди информационных разрядов на определенных местах. В своей простейшей реализации этот код позволяет указать местоположение однократной ошибки и исправить ее. При этом двоичное представление кода ошибки соответствует в десятичной системе счисления номеру разряда, в котором найдена ошибка. Следовательно, легче формализовать процесс корректировки ошибок, а также нет необходимости в составлении таблицы кодов-опознавателей местоположения ошибок и хранении её на приёмной стороне.

Составление кода, с заданным количеством информационных разрядов n и необходимым количеством контрольных разрядов k, начинается с записи контрольных уравнений. Первое контрольное уравнение, по методу Хэмминга, включает те позиции кода, номера которых в двоичном представлении содержат единицу в крайнем правом разряде, т.е. 1 (000 1), 3 (001 1),5 (010 1),…

Второе контрольное уравнение включает позиции, номера которых в двоичном представлении содержат единицу во втором разряде справа, т.е. 2 (00 1 0), 3 (00 1 1),6 (01 1 0), …

Продолжая, таким образом, рассуждения, можно получить следующие контрольные уравнения:

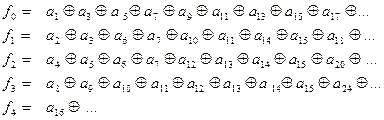
При этом на позициях 1, 2, 4, 8, 16, … располагаются контрольные разряды.

В этом случае не требуется составление проверочной матрицы, поскольку для составления контрольных уравнений она не нужна.

Пример.

Пусть n=4, k=3.

Запишем образующую матрицу:

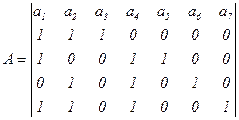
В информационные разряды записывается единичная матрица размером n×n. Контрольные разряды заполняются так, чтобы в результате расчета контрольных уравнений получались нули.

Используя эту матрицу можно получить все необходимые кодовые комбинации путем суммирования строк матрицы по модулю два в различных сочетаниях.

Руководствуясь вышеизложенным алгоритмом, запишем контрольные уравнения:

Допустим, передали комбинацию 3 1 строки: 1 0 1 1 0 1 0, а на приемной стороне получили 1 0 1 0 0 1 0.

Осуществляется проверка:

,

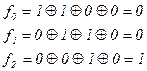Полученная кодовая комбинация записывается в обратном порядке (снизу ввверх) и переводится в число десятичной системы счисления. Получается номер разряда, содержащего ошибку.

f₂ f₁ f₀ = 100 =4₁₀ – ошибка в четвертом разряде (а₄).

После обнаружения ошибки на приемной стороне 4 -й разряд принятой кодовой комбинации должен быть инвертирован (операция «НЕ»), в результате ошибка устраняется.

В компьютерной технике используются более сложные коды Хемминга: после каждых четырех бит данных добавляются три контрольных бита. Такой код Хемминга обеспечивает исправление ошибки в одном бите и определение ошибки в двух следующих битах.

Дата добавления: 2015-07-02