Пояснения к работе

Вопросы для самоподготовки.

1. Статистическая зависимость. Корреляционная зависимость.

2. Корреляционная таблица.

3. Условные и безусловные распределения случайной величины.

4. Понятие об уравнении регрессии. Линейная регрессия.

5. Метод наименьших квадратов.

Статистической зависимостью называют зависимость между двумя случайными величинами, при которой изменение одной из величин влечет за собой изменение закона распределения другой величины. Статистическая зависимость называется корреляционной, если при изменении одной из величин меняет среднее значение другой величины.

Пусть в эксперементе по изучению случайных величин x и yполучены следующие результаты:

· значение x величины x зафиксировано n_x раз;

· значение y величины y зафиксировано n_y раз;

· появление пары значений (x;y) зафиксировано n_(x;y) раз

Полученные результаты удобно представить в виде следующей таблицы, называемой корреляционной таблицей:

Y X	Y1	Y2	…	YP	nx
X1	n (x1;y1)	n (x1;y2)		n (x1;yp)	n x1
X2	n (x2;y1)	n (x2;y2)		n (x2;yp)	n x2
…	…	…	…	…	…
Xk	n (xk; y1)	n (xk; y2)		n (xk; yp)	n xk
ny	ny1	ny2		nyp	n

При изучении случайной величины x можно рассматривать частоты n_x появление её значений x=x вне зависимости от того, какие значения при этом принимает y. Эти частоты определяют безусловное распределение случайной величины x. Кроме того, можно рассматривать и частоты n (x;y) появление значений x=x при определенном значении случайной величины y =y.Они определяют условные распределения случайной величины x. Указанные распределения риведены в корреляционной таблице. Так, каждый столбец y_i таблицы содержит частоты условных распределений при y =y_i. В последнем же столбце n_x находятся частоты безусловного распределения случайной величины x.

Аналогичным образом строки корреляционной таблицы задают условные и безусловные распределения случайной величины y.

Среднее арифметическое значений случайной величины y при x=x называется условной средней y_x. При наличии корреляционной зависимости y от x условная средняя является функцией переменной x. Данную функциональную зависимость, выражаемую уравнением 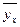= 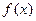, называют уравнением регрессии y на x, а соответствующий график – линией регрессии y на x.

В простейшем случае имеет место линейная регрессия, которая задается уравнением:

=

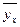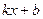
Для выборки, содержащей n пар чисел (x₁:y₁), (x₂;y₂), …,(x_n;y_n), коэффициенты k и b могут быть вычислены методом наименьших квадратов по следующим формулам:

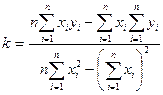
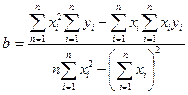
Дата добавления: 2015-07-02