Множественные коэффициенты корреляции и детерминации, их статистический смысл. Точечные оценки и проверка их значимости

Множественный корреляционный и регрессионный анализы. Их место в задачах исследования зависимости между показателями.

Задачи корреляционного анализа многомерной генеральной совокупности:

1. как выбрать с учетом специфики и природы анализируемых переменных подходящий измеритель тесноты статистической связи

2. Как оценить с помощью точечной и интервальной оценок его числовое значение по имеющимся выборочным данным

3. Как проверить гипотезу о том, что полученное значение анализируемого измерителя связи действительно свидетельствует о наличие статистической связи т.е. проверить исследуемую корреляционную характеристику на статистическое значимое отличие от нуля

4. Как определить структуру связей между компонентами исследуемого многомерного признака, сопоставив каждой паре ответ: связь есть или нет.

Характеристики статистической связи, рассматриваемые в корреляционном анализе используются в качестве «входной» информации при решении следующих задаx:

· Определение вида зависимости;

· Снижение размерности анализируемого признакового пространства;

· Классификации объектов и признаков.

Поэтому с корреляционного анализа начинаются все многомерные статистические исследования.

Основная задача корреляционного анализа – выявление связи между переменными и оценка её тесноты.

Основная задача регрессионного анализа – установление формы и изучение зависимости между переменными.

В общем случае многомерной корреляционной модели множественный коэффициент корреляции показывает тесноту связи между одной переменной и многомерным массивом остальных переменных.

Множественный коэффициент детерминации в общем случае многомерной корреляционной модели, например, R_{23/1,2,4,5,…k} показывает долю дисперсии случайной величины X₃, обусловленную влиянием остальных переменных X₁, X₂, X₄, X₅,… X_k, включённых в корреляционную модель.

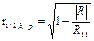- точечная оценка множественного коэффициента корреляции.

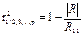- точечная оценка множественного коэффициента детерминации.

Значимость множественного коэффициента корреляции (детерминации) проверяется с помощью F - критерия.

1. Наблюдаемое значение статистики находится по формуле:

2. Нахождение критического значения статистики

3. Вывод по гипотезе

Множественный коэффициент корреляции считается значимым, т. е. имеет место линейная статистическая зависимость, между X₁ и остальными факторами X₂,...,X_р, если: F_набл. > F_кр. (α, р - 1, n – р).

5. Парный и частный коэффициенты корреляции. Их точечные и интервальные оценки. Что общего и в чем различия этих коэффициентов?

Парный коэффициент корреляции, например, между переменной x и y рассчитывается по формуле:

Частный коэффициент корреляции в общем случае многомерной корреляционной модели показывает тесноту связи между двумя рассматриваемыми переменными независимо от влияния фиксируемых остальных l переменных

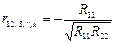
где R_ij – алгебраическое дополнение элемента r_ij корреляционной матрицы R.

Построение с надёжностью γ доверительного интервала для генерального коэффициента корреляции ρmin≤ρ≤ρmax. Используется Z-преобразование Фишера. Z(r) – функция нечётная, Z(-r) = - Z(r)

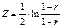
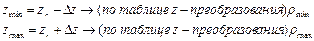
Частный коэффициент корреляции обладает всеми свойствами парного коэффициента корреляции

Парный коэффициент корреляции показывает тесноту связи между переменными X и Y на фоне действия Z.

Частный коэффициент корреляции показывает тесноту связи между переменными X и Y при фиксированной Z (независимо от её влияния).

Дата добавления: 2015-07-02