Момент инерции. Теорема Штейнера

Механика твердого тела

ЛЕКЦИЯ № 08

И биомедицинской техники

«Утверждаю» Заведующий кафедрой _________________ С.И. Шарапов «____»___________ 2010 г.

по разделу «Механика»

учебного курса «Общая физика»

для технических специальностей металлургического факультета

(1 семестр изучения физики)

1. Момент инерции.

2. Теорема Штейнера.

3. Векторное произведение векторов.

4. Моменты инерции однородных тел.

5. Момент силы относительно точки и оси.

6. Кинетическая энергия вращения.

7. Момент импульса и закон его сохранения.

8. Сравнительная таблица основных величин поступательного и вращательного движения.

Составил: _____________ Еремеев Б.Н.

Липецк – 2010

Лекция 08. МЕХАНИКА ТВЕРДОГО ТЕЛА

Момент инерции

Моментом инерции тела (механической системы) относительно оси вращения есть физическая величина, равная сумме произведений масс n материальных точек на квадраты их расстояний до рассматриваемой оси:

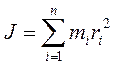
В случае непрерывного распределения масс эта сумма сводится к интегралу, где интегрирование производится по всему объему тела. Величина r в данном случае есть функция положения точки с координатами x, y, z:

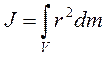
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис.7.1):

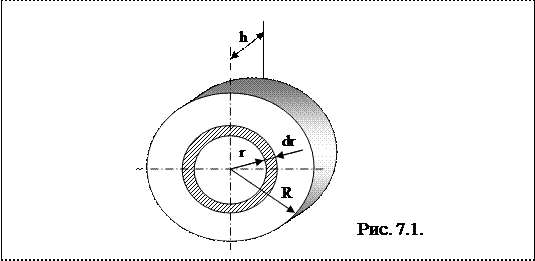
Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r + dr.

Момент инерции каждого полого элементарного цилиндра:

,

т.к. , то считаем, что расстояние всех точек элементарного цилиндра от оси равно 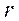. Масса всего элементарного цилиндра – 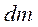, его объем – .

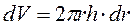Если 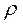- плотность материала, то масса и момент инерции элементарного цилиндра:

, .

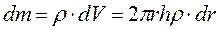Тогда момент инерции сплошного цилиндра:

,

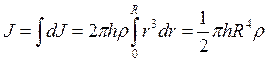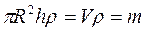но т.к. - объем цилиндра, а , то момент инерции сплошного цилиндра относительно продольной оси:

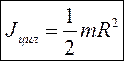
Теорема Штейнера

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:

Момент инерции тела J относительно любой оси вращения равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс тела С, сложенному с произведением массы тела m на квадрат расстояния а между осями:

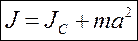
Моменты инерции однородных тел, имеющих массу m, равномерно распределенную по объему, и правильную геометрическую форму:

Тело	Положение оси вращения	Момент инерции
Труба (полый тонкостенный цилиндр) радиуса R	Ось симметрии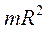
Цилиндр сплошной или диск радиуса R	Ось симметрии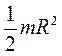
Стержень прямой тонкий, длиной l	Ось перпендикулярна стержню и проходит через его середину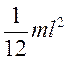
Шар радиусом R	Ось проходит через центр шара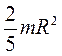

Пример: Найти момент инерции стержня длиной l относительно оси, которая перпендикулярна стержню и проходит через его конец (т.е. ).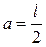

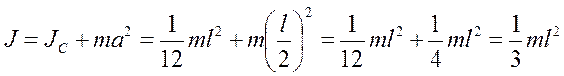
Таким образом, величина момента инерции зависит от выбора оси вращения. Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.

Момент силы

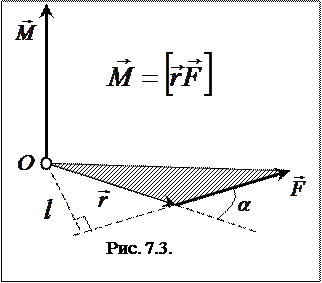
Момент силы относительно неподвижной точки О

- называется физическая величина, определяемая векторным произведением радиуса-вектора 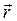, проведенного из точки О в точку А приложения силы, на силу 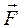(см. рисунок 7.3.):

Здесь 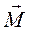- псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 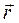к .

Модуль момента силы:

, где

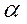- угол между 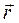и ;

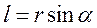- плечо силы - кратчайшее расстояние между линией действия силы и точкой О.

Момент силы относительно неподвижной оси Z

Моментом силы относительно неподвижной оси Z называется скалярная величина , равная проекции на эту ось вектора 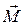момента силы, определенного относительно произвольной точки О данной оси Z (Рис.7.4).

Рис. 7.4.

Значение момента не зависит от выбора положения точки О на оси Z.

Дата добавления: 2015-07-02