Твердого тела

Уравнение динамики вращательного движения

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩЕНИЯ

Абсолютно твердое тело вращается около неподвижной оси Z, проходящей через него (Рис. 7.5). Все точки тела движутся с одинаковой угловой скоростью 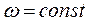. Разбивая тело на элементарные объемы массами

m₁, 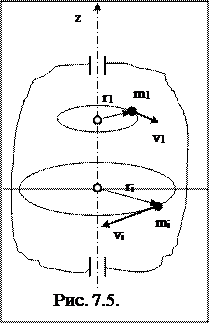m₂, … m_n, находящиеся от оси на расстояниях r₁, r₂, … r_n, получим выражение для кинетической энергии вращения всего тела.

Кинетическая энергия вращения

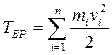, поск. 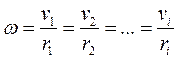, откуда :

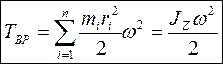
где - момент инерции тела относительно оси Z.

Из сравнения формул 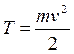и 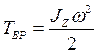следует, что момент инерции – мера инертности тела при вращательном движении.

Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна сумме кинетических энергий этих движений:

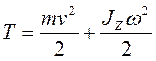
Уравнение динамики вращательного движения

Для вывода уравнения динамики вращательного движения твердого тела рассмотрим элементарную работу вращения, которая идет на увеличение его кинетической энергии:

, в свою очередь , тогда

, делим на dt: , окончательно:

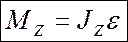В векторном виде: ,

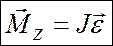где 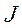- главный момент инерции тела (момент инерции относительно главной оси).

Момент импульса и закон его сохранения

Моментом импульса (количества движения) L материальной точки А относительно неподвижной точки О (рис. 7.6) называется физическая величина, определяемая векторным произведением:

,

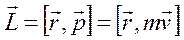Модуль момента импульса:

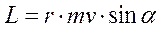
Моментом импульса относительно неподвижной оси Z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса относительно точки О, принадлежащей этой оси. 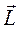- псевдовектор.

Значение момента импульса L не зависит от положения точки на оси Z. При вращении твердого тела вокруг неподвижной оси, каждая точка тела движется по окружности постоянного радиуса 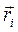со скоростью 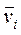перпендикулярной радиусу. Момент импульса отдельной частицы равен: 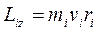и направлен по оси в сторону, определяемую правилом правого винта (совпадает с направлением вектора угловой скорости ).

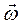Момент импульса твердого тела

Моментом импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Продифференцируем по времени:

В векторной форме: 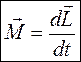- еще одна форма

Дата добавления: 2015-07-02