Введение. Методом крутильных колебаний

Методом крутильных колебаний

И проверка теоремы Штейнера

Определение момента инерции тела

Цель работы: 1) ознакомиться с понятием и методами его определения;

2) изучить метод крутильных колебаний для определения момента инерции тела; 3) применить метод колебаний для экспериментального определения момента инерции твердого тела; 4) проверить теорему Гюйгенса-Штейнера методом крутильных колебаний.

Приборы и принадлежности: установка, секундомер, штангенциркуль, линейка, образцы для измерений.

I. Момент инерции является мерой инертности тела по отношению к вращательному движению; он играет роль, аналогичную роли массы при поступательном движении.

Момент инерции материальной точки относительно какой-нибудь оси вращения называется величина

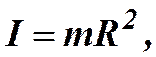(4.1)

где m – масса материальной точки,

R – расстояние точки от оси вращения.

Единица измерения в системе СИ: [ I ] = кгּм².

Момент инерции твердого тела относительно некоторой оси вращения равен сумме моментов инерции элементарных масс, составляющих данное тело:

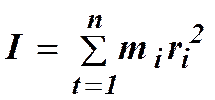, (4.2)

при непрерывном распределении масс: 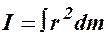. (4.2¹)

Т.о. момент инерции тела зависит от его массы и распределения массы относительно данной оси вращения. Сумма моментов инерций определяется общей массой тела и распределением массы относительно оси вращения: - полое тело или сплошное; как проходит ось вращения относительно тела – через центр масс или нет, или вообще не проходит через тело; параллельно, перпендикулярно или под углом к основанию; однородное тело или нет).

Моменты инерции однородных тел правильной геометрической формы относительно оси, проходящей через центр масс тела, вычисляются дифференциально-интегральным методом и приводятся в справочных таблицах. Некоторые из них приведены в таблице 4.1.

Таблица 4.1

№ п/п	Твердое тело	Положение оси вращения	Момент инерции
1.	Сплошной однородный цилиндр (диск) радиуса r	совпадает с осью симметрии ┴ основанию
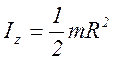
2.	Тонкий однородный диск	совпадает с диаметром диска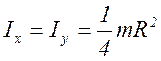
3.	Полый однородный цилиндр (диск) радиуса r	совпадает с осью симметрии ┴ основанию
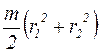
4.	Тонкое кольцо (окружность)	совпадает с осью симметрии ┴ плоскости кольца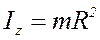
5.	-«»-	совпадает с диаметром кольца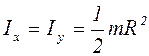
6.	Стержень	через центр стержня ┴ его длине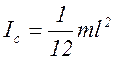
7.	-«»-	через конец стержня ┴ его длине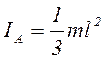
8.	-«»-
9.	Полый шар с тонкими стенками	через центр шара
10.	Сплошной однородный шар	через центр шара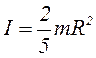

Вычисление момента инерции твердого тела произвольной формы относительно какой-либо оси представляет собой довольно сложную математическую задачу, иногда нерешаемую. Момент инерции системы тел является аддитивной величиной

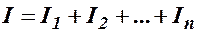, (4.3)

где 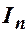- моменты инерции тел, составляющих данную систему.

Моменты инерции твердых тел могут быть определены экспериментально.

II. Одним из методов определения момента инерции твердых тел является метод крутильных колебаний.

Платформа, имеющая форму диска, может совершить крутильные колебания относительно вертикальной оси, проходящей через ее середину.

Рисунок 4.1 – Установка для определения момента инерции методом крутильных колебаний.

При этом центр тяжести платформы перемещается вдоль оси вращения.

Пусть платформа массы , вращаясь в некотором направлении, поднялась на высоту (рис. 4.1) от положения равновесия. Тогда ее потенциальная энергия равна

где g – ускорение силы тяжести.

Предоставленная самой себе платформа возвращается в положение равновесия. При этом ее потенциальная энергия переходит в кинетическую.

Возвратившись в положение равновесия, платформа будет иметь максимальную угловую скорость ω ₀ и кинетическую энергию

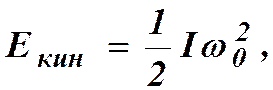
где I – момент инерции платформы относительно оси вращения, перпендикулярной основанию платформы.

Пренебрегая работой сил трения, на основании закона сохранения механической энергии запишем

(4.4)

Определим h и ω₀, подставим в (4.4).

При малой амплитуде колебания платформы можно считать гармоническими. Следовательно, зависимость углового смещения φ от времени t описывается формулой

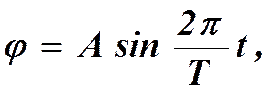(4.5)

где А – амплитуда, т.е. 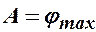- максимальный угол поворота платформы;

Т – период колебаний.

Угловую скорость ω, как функцию времени, можно найти согласно определению углового ускорения

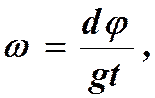
подставим 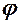и получим:

.

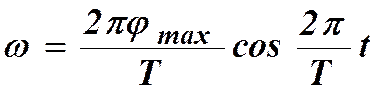Максимальное значение угловой скорости ω _мах = ω ₀, соответствующее моменту времени, когда платформа проходит через положение равновесия и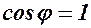

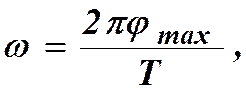(4.6)

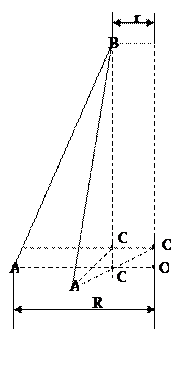Полученное значение максимальной угловой скорости 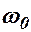подставим в выражение (4.4). Высоту 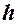будем искать из геометрических соображений.

Рисунок 4.1.

Пусть l – длина нитей подвеса (рис. 4.1), R – расстояние от центра платформы до точек крепления нитей на ней, r – радиус окружности, на которой лежат точки крепления нитей к основанию.

Из рис. 4.1. видно, что

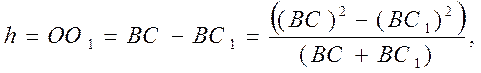
но

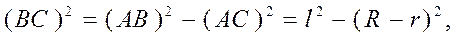
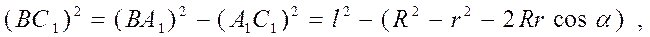Поэтому

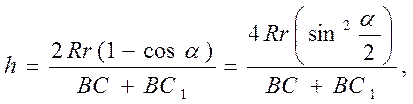
При малых углах смещения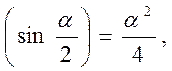

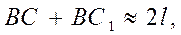
Учитывая это, будем иметь

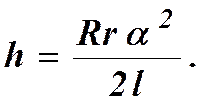(4.7)

Подставив (4.6) и (4.7) в (4.4), получим «рабочую» формулу

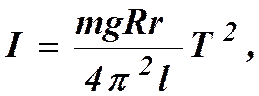(4.8)

которая отражает суть метода крутильных колебаний.

III. В выражении (4.8) величины g, R, r, l, π – постоянные, а период колебаний зависит от массы тела и платформы.

Если на платформу положить тело массы m, то период колебаний изменится. Измерив период колебаний и зная массу тела, можно определить и момонт инерции тела.

При этом следует учитывать, что момент инерции системы (платформа + тело) равен сумме моментов инерции платформы I_пл и момента инерции тела I_m:

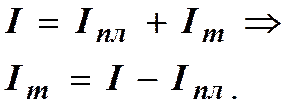(4.9)

Дата добавления: 2015-07-02