Подготовка и проведение измерений

Описание установки

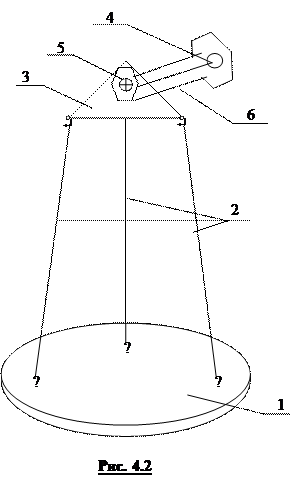
Установка для определения момента инерции тела, которая применяется в данной работе (рис. 4.2), состоит из круглой платформы 1, подвешенной на трех симметрично расположенных длинных нитях 2 (трифилярный подвес). Наверху эти нити прикреплены к основанию 3, имеющему три симметрично расположенных выступа. Основание с помощью болта 5 и упругой пластины 6 соединено с кронштейном 4.

Упражнение 1. Определение момента инерции платформы.

1. Убедитесь в том, что платформа расположена горизонтально.

2. Измерить R, r, l (масса платформы m_пл = (0,815 ± 0,0005)кг).

3. Путем несильного нажатия на край основания 3 (рис. 4.2) сообщить платформе вращательный импульс, относительно оси вращения, перпендикулярной платформе. При помощи секундомера измерить время 10-15 полных колебаний (время определять с точностью до погрешности прибора). Опыт повторить 3-5 раз.

4. Найти период Т_пл этих колебаний и по формуле (4.8) определить момент инерции платформы I_пл. Результаты занести в табл. 4.2.

Таблица 4.2

№ п/п	R м	r м	l м	m кг	N	t с	Тпл с	Тпл с	Iпл кг^.м

5. Платформу нагрузить исследуемым телом, предварительно определив его массу m. Определить период колебаний Т системы (тело + платформа); масса системы (m_пл + m) и момент инерции системы I. Величина момента инерции I_m тела найдется как разность I_m = I - I_пл. Опыт повторить 3-5 раз, результаты измерений занести в таблицу 4.3.

Таблица 4.3

№ п/п	m кг	mпл+m кг	N	t с	Т с	Т с	Iпл кг^.м	Im кг^.м

6. По формуле, взятой из табл. 4.1, вычислить теоретическое значение момента инерции тела и сравнить его со значением, полученным экспериментально.

7. Сделать вывод о возможности определения момента инерции тела произвольной формы методом крутильных колебаний.

Упражнение 2. Проверка теоремы Штейнера

Если сместить ось вращения так, чтобы она не проходила через центр масс, то тело будет участвовать одновременно в двух движениях: относительно оси, проходящей через центр масс, и относительно смещенной оси. Чтобы найти момент инерции тела относительно произвольной оси вращения I, надо к моменту инерции I₀ относительно оси, проходящей через центр инерции на расстояние α от заданной оси вращения и параллельному заданному направлению I₀, прибавить произведение массы m тела на квадрат расстояния α:

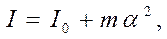(4.10)

- теорема Штейнера.

Теорему Штейнера можно проверить с помощью метода крутильных колебаний.

Так, если поместить тело в центр платформы, то ось вращения будет проходить через центр масс тела. Измерив период колебаний Т по формулам (4.8) и (4.9), определим момент инерции тела относительно оси, проходящей через центр масс I₀. Если поместить тело на платформе на расстоянии α от центра платформы, то ось вращения не будет проходить через центр масс тела. Следовательно, измерив период колебаний и определив момент инерции по формулам (4.8) и (4.9), получим момент инерции относительно произвольной оси I. Подставив I и I₀ в (4.10), убедимся в справедливости выражения (4.10), т.е. теоремы Штейнера.

Выполнение работы

1. Взять два одинаковых тела и определить их момент инерции 2I₂, как указано в упр.1, положив тела одно на другое в центре платформы так, чтобы центры масс тел лежали на одной вертикали с центром масс платформы. Момент инерции оси будет равен I₂. Результаты занести в таблицу 4.4.

Таблица 4.4

№ п/п	m кг	mпл + m кг	N	t с	Т с	Т с	I = 2Im + Iпл кг^.м	Im кг^.м

2. Расположить два тела на некотором расстоянии α друг от друга симметрично относительно центра платформы.

3. Определить расстояние до центра масс одного из тел от оси вращения и его момент инерции I₃ относительно новой оси. Из опыта мы находим момент инерции системы двух тел 2₃. Результаты измерений занести в таблицу 4.5.

Таблица 4.5

№ п/п	m кг	mпл + m кг	N	t с	Т с	Т с	I = 2I3 + Iпл кг^.м	I3 кг^.м

4. Применив теорему Штейнера, проверить равенство

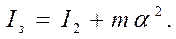(4.11)

Сделать вывод.

5. Вычислить момент инерции I₄ для цилиндра относительно оси вращения, смещенной на расстояние α от центра инерции по формуле (4.10).

6. Сравнить значения I₃, полученные теоретически по формуле (4.10) и экспериментально методом крутильных колебаний (4.11) I₃. Сделать вывод.

7. Найти ошибки экспериментального определения I₂, I₃.

Контрольные вопросы:

1. Бифилярный и трифилярный подвесы. Формулы для определения периодов малых колебаний.

2. Определение момента инерции материальной точки. Момент инерции тела правильной геометрической формы (цилиндра (полого, сплошного), диска, …).

3. Теорема Гюйгенса-Штейнера.

4. Кинетическая энергия вращающегося тела, совершающего поступательное и вращательное движение.

5. Центр масс, центр тяжести.

6. Уравнение гармонических колебаний платформы.

Литература

1. Стрелков С.П. Механика. – Наука. М., 1975. - §§ 54,59,60.

2. Сивухин Д.В. Общий курс физики. Механика. – Наука. М., 1976 - §§ 42,35,36.

Дата добавления: 2015-07-02