Лабораторная работа № 3

ОТЧЕТ

Основные используемые обозначения

Рекомендации и допущения

1. Диапазон напряжений, подаваемых на переход, задается, как правило от –10 до 2 В с шагом 0.01 В. При прямом смещении ток не должен превышать 1 А.
2. Значения диффузионных длин L_n и L_p для конкретного полупроводника взять из базы данных «Ioffe» из раздела «Рекомбинационные параметры».
3. Графики типа W(T,U=const), W(U, T =const) можно строить на одних осях, например, W(U₁=const, T) и W(U₂=const, T). Тогда сразу можно проследить влияние двух аргументов на функцию.
4. Площадь перехода задается произвольно, например, равной 10^-2 мм².

Приложение 1

Символ	Физическая величина	Единица измерения
Apn		Площадь p-n перехода.	мм^2
Dn(Т)		Коэффициент диффузии электронов	см^2·с^-1
Dp(Т)		Коэффициент диффузии дырок	см^2·с^-1
k		Постоянная Больцмана	Дж/К
Na		Заданная концентрация акцепторов в p-области	м^-3
Nd		Заданная концентрация доноров в n-области	м^-3
ni(Т)		Собственная концентрация носителей заряда в полупроводнике	м^-3
Ln		Диффузионная длина электронов	мкм
Lp		Диффузионная длина дырок	мкм
e		Диэлектрическая константа (значение брать из IOFFE\2002\www.ioffe.rssi.ru\SVA\NSM\Semicond\Si\index.html)
e0		Проницаемость вакуума	Ф/м
q		Элементарный заряд электрона	Кл
T		Температура	К
xp, xn		Границы области пространственного заряда	мкм
φ		Напряженность электрического поля	В/м

«Изучение магнитного поля»

(Закон Био-Савара-Лапласа)

Выполнил: студент гр.ХХХ-ХХ __________ //

^{(подпись) (Ф.И.О.)}

Проверил: доцент ___________. /

^{(подпись) (Ф.И.О.)}

Санкт-Петербург

2012 год

Цель работы: измерение магнитных полей, создаваемых проводниками различных конфигураций. Экспериментальная проверка закона Био–Савара–Лапласа.

Краткое теоретическое содержание .

1 ) Магнитное поле прямолинейного проводника с током

Проводник, по которому протекает электрический ток, создает магнитное поле. Магнитное поле характеризуется вектором напряженности `H, который можно вычислить по формуле

`H = òd `H.

Cогласно закону Био-Савара-Лапласа,

,

где I – сила тока в проводнике, d ` l – вектор, имеющий длину элементарного отрезка проводника и направленный по направлению тока, `r – радиус вектор, соединяющий элемент с рассматриваемой точкой P.

Рассмотрим магнитное поле, создаваемое прямолинейным проводником с током конечной длины.

Получим формулу

.

Учитывая, что в настоящей работе длина проводника 2 b много больше расстояния r ₀ от проводника до точки наблюдения магнитного поля, формулу (3) можно записать в виде

.

Поэтому индукция магнитного поля рассчитывается по формуле:

,

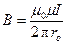где m ₀ – магнитная постоянная, m – магнитная проницаемость среды (для воздуха m = 1)

2) Магнитное поле на оси короткой катушки с током

Короткая катушка – цилиндрическая проволочная катушка, состоящая из N витков одинакового радиуса. Из-за осевой симметрии и в соответствии с принципом суперпозиции магнитное поле такой катушки на оси H представляет собой алгебраическую сумму полей отдельных витков H _i: . Таким образом, магнитное поле короткой катушки, содержащей N _к витков, в произвольной точке оси рассчитывается по формулам

, ,

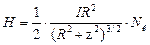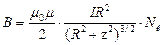где H – напряженность, B – индукция магнитного поля.

3) Магнитное поле соленоида с током

Для расчета индукции магнитного поля в соленоиде используется теорема о циркуляции вектора магнитной индукции:

,

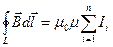где – алгебраическая сумма токов, охватываемых контуром L произвольной формы, n – число проводников с токами, охватываемых контуром

Применим теорему о циркуляции вектора магнитной индукции к соленоиду, длиной l, имеющим N _с витков с силой тока I. В расчете учтем, что практически всё поле сосредоточено внутри соленоида (краевыми эффектами пренебрегаем) и оно является однородным. Тогда формула примет вид:

,

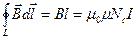откуда находим индукцию магнитного поля, создаваемую током внутри соленоида:

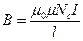
Схема установки

Рис. 1 Принципиальная электрическая схема установки

1 – измеритель индукции магнитного поля (тесламетр), А – амперметр, 2 – соединительный провод, 3 – измерительный щуп, 4 – датчик Холла, 5 – исследуемый объект (короткая катушка, прямой проводник, соленоид), 6 – источник тока, 7 – линейка для фиксирования положения датчика, 8 – держатель щупа.

Дата добавления: 2015-07-02