Частный случай: моделирование дуополии

Основные предпосылки

Модель Штакельберга

Модель Штакельберга — теоретико-игровая модель олигополистического рынка при наличии информационной асимметрии. Названа в честь немецкого экономиста Генриха фон Штакельберга, впервые описавшего ее в работе Marktform und Gleichgewicht (Структура рынка и равновесие), вышедшей в 1934 г.

В этой модели поведение фирм описывается динамической игрой с полной совершенной информацией, что отличает её от модели Курно, в которой поведение фирм моделируется с помощью статической игры с полной информацией. Главной особенностью игры является наличие лидирующей фирмы, которая первой устанавливает объём выпуска товаров, а остальные фирмы ориентируются в своих расчетах на нее.

1. Отрасль производит однородный товар: отличия продукции разных фирм пренебрежимо малы, а значит, покупатель при выборе, у какой фирмы покупать, ориентируется только на цену

2. Фирмы устанавливают количество производимой продукции, а цена на неё определяется исходя из спроса.

3. Существует так называемая фирма-лидер, на объём производства которой ориентируются остальные фирмы.

Пусть существует отрасль с двумя фирмами, одна из которых «фирма-лидер», другая — «фирма-последователь». Пусть цена на продукцию является линейной функцией общего объема предложения Q:

.

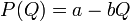Предположим также, что издержки фирм на единицу продукции постоянны и равны с ₁ и с ₂ соответственно. Тогда прибыль первой фирмы будет определяться формулой

,

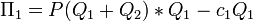а прибыль второй соответственно

.

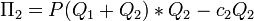В соответствии с моделью Штакельберга, первая фирма — фирма-лидер — на первом шаге назначает свой выпуск Q ₁. После этого вторая фирма — фирма-последователь — анализируя действия фирмы-лидера определяет свой выпуск Q ₂. Целью обеих фирм является максимизация своих платёжных функций.

Равновесие Нэша в этой игре определяется методом обратной индукции. Рассмотрим предпоследний этап игры — ход второй фирмы. На этом этапе фирма 2 знает объем оптимального выпуска продукции первой фирмой Q ₁^*. Тогда задача определения оптимального выпуска Q ₂^* сводится к решению задачи нахождения точки максимума платёжной функции второй фирмы. Максимизируя функцию Π₂ по переменной Q ₂, считая Q ₁ заданным, находим, что оптимальный выпуск второй фирмы

.

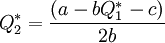Это наилучший ответ фирмы-последователя на выбор фирмой-лидером выпуска Q ₁^*. Фирма-лидер может максимизировать свою платёжную функцию, учитывая вид функции Q ₂^*. Точка максимума функции Π₁ по переменной Q ₁ при подстановке Q ₂^* будет

.

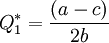Подставляя это в выражение для Q ₂^*, получим

.

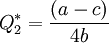Таким образом, в равновесии фирма-лидер производит в два раза большее количество продукции, нежели фирма-последователь.

Дата добавления: 2015-07-02