Минимизация комбинационных логических устройств

Лекция №11

1. Описание ФАЛ в виде последовательности десятичных или двоичных чисел. Описание ФАЛ в виде кубических комплексов

2. Теорема поглощения и теорема склеивания – основные теоремы минимизации ФАЛ

3. Минимизация ФАЛ методом Квайна

4. Минимизация ФАЛ методом кубических форм

5. Минимизация ФАЛ методом карт Карно (Вейча)

1. Описание ФАЛ в виде последовательности десятичных или двоичных чисел. Описание ФАЛ в виде кубических комплексов

1.1 ФАЛ óКЛС.

ФАЛ, выраженные в СДНФ и СКНФ, описывают алгоритм работы КЛС, которые могут быть созданы на любой базисной комбинации элементарных логических элементов.

Как правило, КЛС, созданные с использованием СДНФ и СКНФ, обладают аппаратной избыточностью.

Поэтому при проектировании КЛС с целью минимизации (упрощения) логических функций используют методов:

А) метод Квайна;

Б) метод кубических форм;

В) метод карт Карно (карт Вейча);

Г) метод Мак-Класки - специальный алгоритмически метод минимизации на ЭВМ.

1.2 Способы описания ФАЛ:

а) словесное описание;

Таблица 1
X2	X1	X0	y

б) в виде таблиц истинности (Таблица 1);

в) в виде алгебраического выражения:

ДНФ, КНФ, СДНФ,СКНФ;

г) описание в виде последовательности

десятичных или двоичных чисел:

y(x3,x2,x1,x0)=Σ(4,5,6,9)=V(4,5,6,9)=

V(0100,0101,0110,1001);

y=(x3,x2,x1,x0)=П(2,3,7,5)=∩(2,3,7,5);

д) представление в виде кубических комплексов:

0-кубы (нулевые кубы)

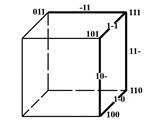1-кубы (единичные кубы)

2-кубы (двоичные кубы)

y(x2,x1,x0)= Σ(3,4,5,6,7)=V(011,100,101,110,111);

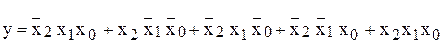
1.3 Кубы, отличающиеся только одной переменной, называются соседними.

Ранг куба определяется числом несовпадающих переменных координат – числом прочерков.

1.4 Нулевой кубический комплекс K₀ - множество “0”кубов:

К0= Σ(011,100,101,110,111)

1.5 Единичный кубический комплекс К1- множество единичных кубов:

К1= Σ(-11,10-,1-0,11-,1-1):

1.6 Двоичный кубический комплекс К2 - множество двоичных кубов:

К2= Σ(1- -)

1.7. Кубический комплекс К(Z) образуется сложением кубических комплексов К₀,К₁,…,К_n-1

Кубический комплекс К(Z) для нашего примера:

K(Z)=(011,100,101,110,111,-11,11-,1-1,10-,1-0,1- -)

1.8 Покрытием П(Z) называют подмножество кубов из комплекса К(Z ) разных рангов.

1.9 Цена любого n-куба ранга r, входящего в П(Z),равна:

Ц_k=(n-r)_k

n-число переменных куба; r-ранг куба.

1.10 Цена покрытия П(Z) равна:

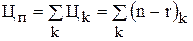
Дата добавления: 2015-07-02