Теория метода и вывод рабочей формулы

В данной лабораторной работе используется метод определения ускорения свободного падения, основанный на измерении периода колебаний маятника, представляющего собой металлический шарик, подвешенный на тонкой длинной нити.

В физике маятником называется любое твёрдое тело, совершающее колебания под действием силы тяжести вокруг неподвижной оси, не проходящей через центр тяжести тела. Различают математический и физический маятники.

Математическим маятником называется материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая под действием силы тяжести колебания в вертикальной плоскости. Практически математическим маятником можно считать груз, подвешенный на нерастяжимой нити, если размеры груза очень малы по сравнению с длиной нити, а масса нити очень мала по сравнению с массой груза.

Если колеблющееся тело нельзя рассматривать как материальную точку, то маятник называется физическим.

Время одного полного колебания маятника называется периодом колебаний и обозначается буквой Т.

Рассмотрим колебания математического маятника (рис. 3).

Отклонение маятника от положения равновесия будем характеризовать углом j, образованным нитью с вертикалью. При отклонении маятника на угол j возникает вращающий момент силы тяжести, равный, по определению, произведению силы на плечо:

М = mg 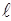sinj, (4)

где 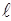sinj - плечо силы тяжести.

Если угол j мал, то можно положить sinj = j. В результате, уравнение (4) принимает вид

М = mg 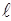j. (5)

При отклонении маятника вправо от положения равновесия, вращающий момент М будет стремиться повернуть маятник влево, а при отклонении маятника влево - вращающий момент будет стремиться повернуть маятник вправо. Поэтому вращающему моменту М и угловому смещению jнужно приписывать противоположные знаки. В результате, уравнение (5) записывается в виде

М = - mg 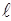j. (6)

Напишем для маятника уравнение динамики вращательного движения:

М = Ie, (7)

где I - момент инерции маятника относительно оси вращения; e - угловое ускорение.

Так как для материальной точки относительно оси вращения I = m 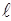², а 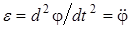, то из (6) с учётом (7) получим

,

откуда

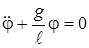. (8)

Введём обозначение

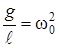. (9)

С использованием (9) уравнение (8) принимает вид

. (10)

Уравнение (10) представляет собой дифференциальное уравнение колебаний математического маятника, решение которого имеет вид

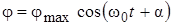, (11)

где a - начальная фаза; j_max - амплитуда колебания; w₀ - циклическая частота колебаний.

Таким образом, при малых углах j, математический маятник совершает гармонические колебания (11) с циклической частотой и периодом Т, равным

,

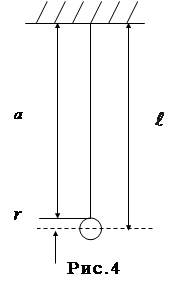
откуда находим (12)

Для лабораторного маятника с металлическим шариком радиуса r и длиной нити, равной a (рис. 4) имеем

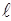= a + r, (13)

Момент инерции такого маятника относительно оси качания равен

I = I_с + m 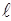²= 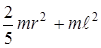, (14)

где I_{с =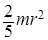} - момент инерции металлического шарика относительно оси, проходящей через его центр; m - масса шарика; ml² - момент инерции шарика относительно оси качания.

С учётом (13), (14) из (6) и (7) получаем

,

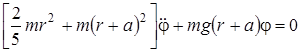или

где , .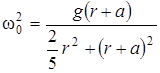

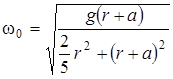В результате, период колебания такого маятника равен

, откуда 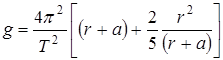. (15)

При радиусе шарика порядка 1 см и длине нити 100 см различие в результатах расчёта по формулам (16) и (20) составляет 0,004%, а при длине нити 40 см - около 0,01%.

Дата добавления: 2015-07-02