Ротор магнитного поля

Дивергенция магнитного поля

До настоящего времени экспериментально обнаружить магнитные заряды не удалось. Соответственно линии вектора 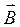не имеет ни начала, ни конца и всегда замкнуты. Соответственно поток 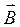через любую замкнутую поверх­ность должен быть равен нулю. Таким образом, теорема Гаусса в интегральной форме для вектора 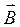выражается формулой:

(18.40)

– поток вектора магнитной индукции через любую замкнутую поверхность ра­вен нулю.

Преобразуем поверхностный интеграл в (18.40) по теореме Остроградского-Гаусса:

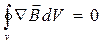(18.41)

Уравнение (18.41) должно выполняться для произвольного объема, а поэтому

(18.42)

Соотношение (18.42)выражает теорему Гаусса в дифференциальной форме для вектора индукции магнитного поля.

Циркуляция вектора 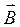наиболее просто вычисляется в случае прямого тока. Рассмотрим замкнутый контур, лежащий в плоскости, перпендикулярной к току. В каждой точке контура 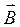направлен по касательной к окружности с центром в месте прохождения тока и проходящей через данную точку. В выражении для циркуляции заменим 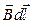на . Учтем, что - угол, на который поворачивается радиаль­ная прямая при перемещении вдоль контура на . Таким образом,

(18.43)

Тогда для циркуляции получаем

(18.44)

Если рассматриваемый контур охватывает ток, то при обходе по контуру ра­диальная прямая поворачивается в одном направлении и . Если же контур не охватывает тока, то 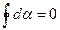. Поэтому можно записать:

(18.45)

где под I подразумевается ток, охватываемый контуром.

В выражении (18.45) ток рассматривается как алгебраическая величина: если направление обхода контура образует с направлением тока правовинтовую систему, то ток считают положительным, в противном случае - отрицательным.

Формула (18.45) получена для прямого тока. Но можно доказать, что онасправедлива и в общем случае, для тока произвольной формы.

Представим, что некоторый контур охватывает не один а несколько токов. Для каждого из них справедливо соотношение (18.45). В соответствии с принципом суперпозиции индукция результирующего поля 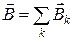равна векторной сумме полей каждого из этих токов. Поэтому циркуляция вектора индукции результирующего поля 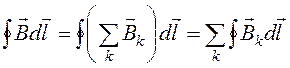(18.46)

По формуле (18.45)

(18.47)

Важно помнить, что сумма в (18.47) является алгебраической.

Возможны ситуации, когда токи распределены в пространстве с некоторой плотностью 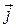. Этом случае вместо в (18.47) следует взять ток, который протекает через некоторую поверхность , опирающуюся на контур L. При этом поверхность может быть произвольной, единственное требование – она должна опираться на контур L. Суммарный ток через такую поверхность равен потоку вектора 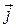через нее. Поэтому соотношение (18.47) можно представить в виде:

(18.48)

По теореме Стокса

. (18.49)

Следовательно

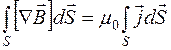. (18.50)

Поверхность интегрирования может быть произвольной (опирающуйся на контур L), поэтому должны быть равны подынтегральные выражения:

. (18.51)

Формулы (18.48) и (18.51) отражают существенное отличие электрического и магнитного полей: циркуляция и ротор вектора напряженности электрического поля равны нулю. Это является следствием того, что электростатическое поле потенциально и может быть описано с помощью скалярного потенциала.

Магнитное поле не является потенциальным, его циркуляция не обязательно равна нулю, его нельзя описать с помощью скалярного потенциала. Такие поля называют вихревыми или соленоидальными.

Дата добавления: 2015-07-02