Движение заряженных частиц в магнитном поле

Выражение для силы Лоренца (114.1) по­зволяет найти ряд закономерностей дви­жения заряженных частиц в магнитном поле. Направление силы Лоренца и на­правление вызываемого ею отклонения за­ряженной частицы в магнитном поле за­висят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.

Для вывода общих закономерностей будем считать, что магнитное поле одно­родно и на частицы электрические поля не действуют. Если заряженная частица дви­жется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В ра­вен 0 или p. Тогда по формуле (114.1) сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она дви­жется равномерно и прямолинейно.

Если заряженная частица движется в магнитном поле со скоростью v, перпен­дикулярной вектору В, то сила Лоренца F =Q[ vB ] постоянна по модулю и нор­мальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяет­ся из условия

QvB = mv²/r,

откуда

Период вращения частицы, т. е. вре­мя Т, затрачиваемое ею на один полный оборот,

T = 2nr/v.

Подставив сюда выражение (115.1), по­лучим

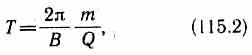
т. е. период вращения частицы в однород­ном магнитном поле определяется только величиной, обратной удельному заряду

(Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v << с)). На этом основано действие цикли­ческих ускорителей заряженных частиц (см. §116).

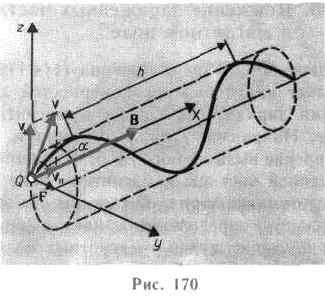
Если скорость v заряженной частицы направлена под углом а к вектору В (рис. 170), то ее движение можно пред­ставить в виде суперпозиции: 1) равно­мерного прямолинейного движения вдоль поля со скоростью v_||=vcosa; 2) равно­мерного движения со скоростью v _┴= v sina по окружности в плоскости, пер­пендикулярной полю. Радиус окружности определяется формулой (115.1) (в данном случае надо заменить v на v_┴=vsina). В результате сложения обоих движений возникает движение по спирали, ось кото­рой параллельна магнитному полю (рис. 170). Шаг винтовой линии

h=v _|| T=vT cosa.

Подставив в последнее выражение (115.2), получим

h=2pmv cosa/(BQ).

Направление, в котором закручивается спираль, зависит от знака заряда ча­стицы.

Если скорость v заряженной частицы составляет угол а с направлением векто­ра В неоднородного магнитного поля, ин­дукция которого возрастает в направле­нии движения частицы, то r и h уменьша­ются с ростом В. На этом основана фокусировка заряженных частиц в маг­нитном поле.

Дата добавления: 2015-07-02