Оценка правильности и воспроизводимости. Нормальное распределение. t-Распределение

Правильность, воспроизводимость и точность анализа

Систематическая погрешность определяет важнейшее понятие – правильность, а случайная погрешность – воспроизводимость.

Правильность измерений – это качество измерений, отражающее близость к нулю систематической погрешности.

Сходимость измерений – это качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях.

Воспроизводимость измерений – это качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях (в разное время, разными методами, разными аналитиками и т.д.).

Проиллюстрируем правильность и воспроизводимость на примере стрельбы трех стрелков в тире.

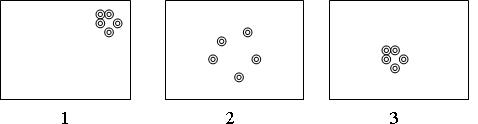
воспроизводимо, но неправильно

невоспроизводимо (кучность стрельбы плохая), но правильно

правильно и воспроизводимо - точно

Точность измерений – это качество измерений, отражающее близость их результатов к истинному (действительному) значению измеряемой величины или близость к нулю систематической и случайной погрешностей.

В результате проведенного химического анализа получены х₁, х₂,…, х_n – результаты параллельных определений компонента в пробе одним и тем же методом. В ряду параллельных определений нередко обнаруживается результат анализа, резко отличающийся от других результатов и от среднего арифметического. Произвольное отбрасывание измерения, которое является «слишком» высоким или «слишком» низким, может существенно исказить результат анализа, так же как и включение ошибочных данных в расчет среднего арифметического. Для решения вопроса – оставить результат или отбросить– существует несколько алгоритмов.

Обнаружение промахов по Q-критерию.

Ранжируют параллельные результаты по возрастающей:

х₁, х₂,…, х_n

Вычисляют размах варьирования (разность между максимальным и минимальным результатами):

R = х_n– х₁

Находят значение критерия Q:

,

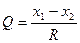где х₁ – подозрительно выделяющееся (сомнительное) значение; х₂ – соседнее с ним значение.

Рассчитанная величина Q сравнивается с Q_табл – табличным значением критерия при данных вероятности и числе свободы. Если Q > Q_табл, подозреваемый результат является грубо ошибочным и его следует исключить при расчете среднего арифметического. Если Q < Q_табл, результат оставляют.

Количественная оценка воспроизводимости.

Среднее арифметическое значение:

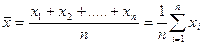
Рассеяние случайной величины относительно среднего значения характеризуется дисперсией S²:

,

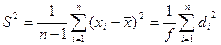где d – отклонение; f = n – 1 – число степеней свободы. Это число независимых измерений за вычетом числа связей, наложенных на эту систему при обработке материала. В данном случае одна связь, наложенная при расчете среднего значения. Если бы, например, генеральное среднее было заранее известно, то число степеней свободы при определении дисперсии было бы просто равно числу измерений, поскольку наложения связи 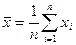не было бы.

Если число результатов очень велико, величина S² стремится к некоторому постоянному значению σ² – дисперсии измерения. А величина S² является выборочной дисперсией измерения. Однако дисперсия в явном виде не может использоваться для количественной характеристики рассеяния результатов, поскольку ее размерность не совпадает с размерностью результата анализа.

Для характеристики рассеяния используют стандартное отклонение (или среднее квадратичное (или квадратическое) отклонение):

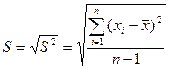
Относительное стандартное отклонение:

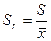
Это безразмерная величина, объективный показатель воспроизводимости.

Все три величины – дисперсия, стандартное отклонение и относительное стандартное отклонение – характеризуют воспроизводимость результатов химического анализа, т.е. определяются случайной погрешностью.

Одной из основных задач аналитика при оценке случайных погрешностей химического анализа является нахождение функции распределения, которой описываются экспериментальные данные. Многочисленными исследованиями показано, что данные большинства аналитических определений при наличии генеральной совокупности результатов химического анализа подчиняются закону нормального распределения (распределение Гаусса). Графическое изображение нормального распределения случайной величины x:

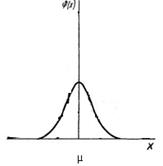
φ(х) – плотность вероятности; х – значение случайной величины; µ – генеральное среднее.

Видно, что кривая имеет колоколообразный вид, она симметрична относительно вертикальной линии, проходящей через µ. Характер кривой зависит от величины дисперсии: чем больше дисперсия σ², тем более пологой становится кривая.

В соответствии с законом нормального распределения вероятность появления малых погрешностей значительно больше, чем вероятность появления больших погрешностей. Однако при небольшом числе наблюдений (параллельных проб) большие погрешности обычно не появляются, что приводит к занижению погрешности при обработке результатов в соответствии с нормальным распределением.

Более корректная величина погрешности получается при использовании статистики малых выборок (t-распределение или распределение Стьюдента). Это распределение предусматривает большую вероятность появления больших погрешностей и меньшую вероятность малых погрешностей, чем в нормальном распределении.

Как и нормальное распределение, t -распределение симметрично и имеет максимум при том же значении абсциссы, при котором он был при нормальном распределении. Но высота и ширина этого распределения зависят от числа степеней свободы, т.е. от числа измерений:

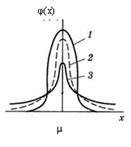1) f = ∞; 2) f = 7; 3) f = 3

чем меньше число степеней свободы, тем меньше крутизна кривой и тем медленнее она сближается с осью абсцисс при одном и том же стандартном отклонении. При f → ∞ t -распределение переходит в нормальное распределение.

Количественная оценка правильности

Для оценки правильности могла бы служить разница между действительной величиной и найденным нами средним арифметическим. Однако обычно действительное значение определяемой величины неизвестно. Для оценки правильности используют доверительный интервал.

Доверительный интервал – это интервал значений, в котором находится действительное (достоверно установленное) содержание с определенной степенью надежности Р.

Статистическая надежность Р, или доверительная вероятность, – это число, показывающее, сколько результатов из 100 параллельных измерений попадает в интервал.

При заданной доверительной вероятности Р доверительный интервал составляет 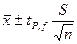, где t_P,f – коэффициент Стьюдента, учитывающий разницу в нормальном и t -распределении и при данном Р зависящий от числа степеней свободы.

Если действительное содержание определяемого компонента, известное, например, из свидетельства к стандартному образцу, попадает в доверительный интервал, значит, методика не имеет систематической погрешности, она правильна.

В 1993 г. Международная организация по стандартизации (ISO) издала «Руководство по выражению неопределенности измерений». На Украине появились нормативные документы, согласно которым неопределенность является уже не рекомендуемой, а обязательной характеристикой результатов любых измерений. Согласно рассматриваемой концепции, мы не знаем и никогда не узнаем ни истинного значения измеряемой величины, ни погрешностей результата ее измерения. Введение понятия «неопределенность» вместо привычной «погрешности» в основном направлено на то, чтобы устранить разделение погрешностей на случайные и систематические: неопределенность включает в себя как те, так и другие.

Дата добавления: 2015-07-02