ЛЕКЦИЯ №6

Форма.

Форма

Форма

В том случаи, если погрешность подразделяется систематическую и случайную: - результат измерения.

- нижняя и верхняя границы.

доверительная вероятность.

стандартная аппроксимация функции плотности вероятности. .

Пример: 31,5 В, Р(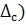 =0,95. 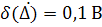; равн.

- результат измерения;

- оценки С.К.О. систематической и случайной составляющей;

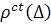- стандартная аппроксимация плотности распределения.

Пример: 25,12 В,

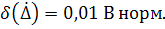
- результат измерения;

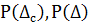- плотности вероятности системной и случайной составляющей.

Формы представления нормированных МХ.

1.Номинальную функцию 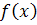преобразования измерительного преобразователя представляют в виде формулы, таблицы, графиков.

2.Номинальное значение… целыми числами.

3.Линейную функцию преобразования… представляется коэффициентом преобразования в виде чисел.

4. Нормированную МХ погрешности СИ представляют числом или функцией в виде(формулы, таблицы, графика) информативным параметром входного или выходного сигнала для абсолютной, относительной или…погрешности.

5. Нормированный предел 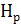вариационной СИ представляют числом в арифметической измеряемой величиной или в %-тах.

6. Функцию и плотность реализации в виде формулы, таблицы и графика.

7.Номинальную функцию влияния, пределы отклонений от неё и графическую функцию представляют в виде числа, формулы, таблицы, графика.

Основные принципы:

1.Погрешность СИ рассматривают как случайные величины. Согласно этому принципу ГОСТ 8.009-84 вводит статистические методы информации МХ СИ.

2. Различают МХ характеристики типа и конкретного измерительного прибора.

А)для типа измерительных систем погрешности являются случайной величиной, поэтому они могут нормироваться но только измерениями по М() и ().

Б)для конкретного эксперимента –детерминированная величина.

3.Сиситематические и случайные погрешности нормируются раздельно.

Комплексы нормирования МХ.

КЛАССЫ ТОНЧОСТИ СРЕДСТВ ИЗМЕРЕНИЙ

Погрешности СИ классифицируют по следующим признакам:

1. По способу выражения погрешности подразделяют на абсолютные, приведенные и относительные.

А) абсолютной погрешностью СИ называют разность между его показанием и истинным значением измеряемой величины Х.

.

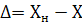Б) приведенная погрешность СИ равна отношению абсолютной погрешности к нормирующему значению 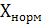и выражается обычно в %-тах.

Нормирующее значение 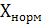устанавливается в зависимости от характера шкалы.

1)при 0-ой отметке на краю или вне диапазона – большему из пределов измерения;

2) при нулевой отметке внутри диапазона – сумме модулей пределов;

3) при существенно не равномерной шкале – всей длине шкалы;

4) при установленном номинальном значении – номинальному значению.

В) относительная погрешность СИ равна отношению абсолютной погрешности к истинному значению измеряемой величины:

2. По характеру измерения погрешности подразделяют на систематические и случайные.

3. По условиям возникновения погрешности делят на основные и дополнительные.

Предел допускаемой погрешности СИ - наибольшая его погрешность, при которой СИ может быть призвано годным и допущено к применению.

Класс точности – это обобщенная характеристика СИ, определяющая пределы допускаемых основных и дополнительной погрешности.

В обозначениях класса точности используются числа, которые характеризуют предел допускаемой погрешности в виде абсолютной, относительной или приведенной погрешности, а так же латинскими буквами или римскими цифрами.

СПОСОБЫ НОРМИРОВАНИЯ ПРЕДЕЛОВ (ДП)

ГОСТ 8.401-80 устанавливает следующие основные способы установления пределов допускаемых погрешностей.

1.Для СИ с неизменными границами абсолютной погрешности предел принято выражать в форме абсолютной погрешности:

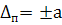
Класс точности обозначается латинскими буквами(или римскими буквами).

Пример – многозначные меры.

2. Для СИ с неизменными границами абсолютной погрешности, у которых нормирующее значение выражено в единицах измеряемой величины, предел выражается в форме приведенной погрешности.

Она определяется по одночленной формуле:

Класс точности – это число р %, совпадающее с приведенной погрешностью. Число р - отвлеченное положительное число, выбираемое из ряда 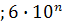(n=1,0,-1,-2)

Пример: показывающие и самопищущие приборы.

3.Для СИ, у которых неизменны границы относительной погрешности, предел допускаемой погрешности следует выражать в форме относительной погрешности. Класс точности обозначают числом, заключенным в кружок и равным пределу погрешности в %-тах.

Пример: однозначная мера, счетчик энергии.

4. Для СИ, у которых границы абсолютной погрешности можно полагать изменяющимися практически линейно в зависимости от значения измеряемой величины.

).

Пределы допускаемой погрешности следует выражать в форме относительной погрешности по двухчленной формуле:

,

Где ; с = b +d= ;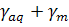

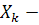наибольший из пределов.

Класс точности обозначают двумя числами, выраженными c и d в %-тах и разделенные косой чертой.

Например: 0,02/0,01

5.Для СИ, у которых шкала существенно не линейна и границы абсолютной погрешности, выраженные в единицах длины шкалы практически не измены, пределы допускаемой основной погрешности принято выражать в форме приведенной погрешности.

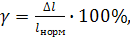
где выражается в единицах шкалы.

Класс точности выражается одним числом в %-тах, помещенными над «углом»().

c=b+d, приведенная аддитивная составляющая.

Установленные обозначения классов точности по пределам допускаемых погрешностей.

Формула для определения пределов допускаемых погрешностей	Примеры пределов допускаемой основной погрешности	Обозначение класса точности	Примечание
В документации	На средствах измерения
	-	Класс точности М	М	-
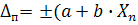
	-	Класс точности С	С	-
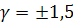
		Класс точности 1,5	1,5	Если выражено в единицах величины
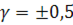
	Класс точности 0,5	0,5	Если определяется длиной шкалы
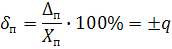
		Класс точности 0,5	0,5	-
		Класс точности 0,02/0,01	0,02/0,01	-

Р =

(n=1,0,-1,-2)

Формулы выражения погрешности	Придел допускаемой погрешности	Обозначение класса точности(для данного прибора)
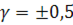
Приведенная погрешность(если выражена в единицах измеряемой величины)		1,5
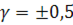
Приведенная погрешность(если принята равной длине шкалы)		0,5
Относительная погрешность		0,5
Относительная погрешность, возрастающая с уменьшением измеряемой величины		0,02/0,01

ЛЕКЦИЯ № 7

Дата добавления: 2015-07-02