Эквивалентность МП-автоматов и КС-грамматик

Теперь можно показать, что языки, определяемые МП-автоматами - это в точности КС-языки. Начнем с построения естественного (недетерминированного) “нисходящего” распознавателя, эквивалентного данной КС-грамматике.

Теорема 6.2. Пусть G=( N, S, P, S) - КС-грамматика. По грамматике G можно построить такой МП-автомат R, что L(R)=L(G).

Доказательство. Построим R так, чтобы он моделировал все левые выводы в грамматике G.

Пусть R=({q}, S, N È S, d, q, S, Æ), где d определяется следующим образом:

(1) если A ® a принадлежит P, то d (q, e, A) содержит (q, a);

(2) d (q, a, a) = {(q, e) для всех aÎ S.

Необходимо показать, что

A Þ ^m w

тогда и только тогда, когда

(q, w, A) ú¾ ⁿ (q, e, e)

для некоторых m, n ³ 1.

Необходимость условия доказывается индукцией по m. Допустим, что A Þ ^m w. Если m=1 и w = a₁ ... a_k (k ³ 0), то

(q, a₁ ... a_k , A) ú¾ (q, a₁ ... a_k, a₁ ... a_k)

ú¾ ^k (q, e, e)

Теперь предположим, что A Þ ^m w для некоторого m>1. Первый шаг этого вывода должен иметь вид A Þ X₁ X₂ ... X_k, где 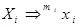для некоторого m _i < m, 1£ i £ k, и x₁ x₂ ...x_k = w. Тогда

(q, w, A) ú¾ (q, w, X₁ X₂ ... X_k )

Если X_i Î N, то по предположению индукции

(q, x_i , X_i ) ú¾ ^* (q, e, e)

Если X_i Î S, то

(q, x_i , X_i ) ú¾ (q, e, e)

Объединяя все эти последовательности тактов, видим, что

(q, w, A) ú¾ ⁺ (q, e, e).

Для доказательства достаточности покажем индукцией по n, что если

(q, w, A) ú¾ ⁿ (q, e, e),

то

A Þ ⁺ w.

Если n=1, то w = e и A ® e принадлежит P. Предположим, что утверждение верно для всех n^½< n. Тогда первый такт, сделанный МП-автоматом R, должен иметь вид

(q, w, A) ÷¾ (q, w, X₁ ... X_k )

причем (q, x_i , X_i ) ú¾ 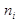(q, e, e) для 1£ i £ k и w = x₁ x₂ ... x_k . Тогда A ® X₁ ... X_k - правило из P, и по предположению индукции X_i Þ ⁺ x_i для X_i Î N. Если X_i Î S, то X_i Þ ⁰ x_i. Таким образом

A Þ X₁ ... X_k

Þ ^* x₁ X₂ ... X_k

........................

Þ ^* x₁ x₂ ... x_k-1 Xk

Þ ^* x₁ x₂ ... x_k-1 x_k = w

- вывод цепочки w из A в грамматике G. ž

Пример 6.4. Построим МП-автомат R, для которого L(R) = L(G₀ ), где G₀ - грамматика, определяющая арифметические выражения с правилами

E ® E+T ½ T

T ® T * F ½ F

F ® (E) ½ a

Пусть R = ({q}, S, G, d, q, E, Æ), где d определяется так:

(1) d (q, e, E) = {(q, E+T), (q, T)};

(2) d (q, e, T) = {(q, T * F), (q, F)};

(3) d (q, e, F) = {(q, (E)), (q, a)};

(4) d (q, b, b) = {(q, e)} для всех bÎ {a, +, *, (,)}.

При выводе a+a * a для R возможна среди других следующая последовательность тактов:

(q, a+a * a, E) ÷¾ (q, a+a * a, E+T)

÷¾ (q, a+a * a, T+T)

÷¾ (q, a+a * a, F+T)

÷¾ (q, a+a * a, a+T)

÷¾ (q, +a * a, +T)

÷¾ (q, a * a, T)

÷¾ (q, a * a, T * F)

÷¾ (q, a * a, F * F)

÷¾ (q, a * a, a * F)

÷¾ (q, * a, * F)

÷¾ (q, a, F)

÷¾ (q, a, a)

÷¾ (q, e, e)

Заметим, что вычисление МП-автомата R соответствует левому выводу цепочки a+ a* a из E в грамматике G₀. 

Тип синтаксического анализа, проводимого МП-автоматом, построенным в теореме 6.2, называется “нисходящим анализом” (“анализом сверху вниз”) или “пред­ска­зы­ва­ю­щим анализом”, потому что при этом дерево вывода строится по существу сверху (от корня) вниз, а каждый такт вида (1) можно трактовать как предсказание очередного шага левого вывода. Подробно нисходящий синтаксический анализ и его алгоритмы, как часть компилятора, будут рассмотрены во второй части пособия.

Можно построить расширенный МП-автомат, который работает “снизу вверх” как “восходящий анализатор”, моделируя в обратном порядке правые выводы в КС-грамматике. Рассмотрим цепочку a+a * aÎ L(G₀ ) из примера 6.4 и ее правый вывод из E в грамматике G₀ :

E Þ E+T Þ E+T * F Þ E+T * a Þ E+F * a

Þ E+a * a Þ T+a * a Þ F+a * a Þ a+a * a

Предположим, что мы записываем этот вывод в обратном порядке. Если считать, что переход от цепочки a+a * a к цепочке F+a * a происходит по правилу F ® a, примененному “в обратном направлении”, то можно сказать, что цепочка a+a * a “сверты­ва­ется (редуцируется) слева” к цепочке F+a * a. Более того, это единственно возможная левая свертка. Подобным же образом можно правовыводимую цепочку F+a * a свернуть слева к цепочке T+a * a с помощью правила T ® F и т.д. Определим формально левую свертку.

Пусть G=( N, S, P, S) - КС-грамматика и

S Þ ^* aAg Þ abg Þ ^* cg

- правый вывод в ней. Говорят, что правовыводимую цепочку abg можно свернуть слева (редуцировать) к правовыводимой цепочке aAg с помощью правила A ® b. Указанное вхождение цепочки b в цепочку abg называется основой цепочки abg.

Таким образом, основа правовыводимой цепочки - это ее любая подцепочка, которая является правой частью некоторого правила, причем после замены ее левой частью этого правила тоже получится правовыводимая цепочка.

Основу правовыводимой цепочки можно было определить другим способом в терминах деревьев вывода.

Основа - это крона самого левого поддерева глубины 1 некоторого дерева вывода заданной правовыводимой цепочки.

Дерево глубины 1, состоящее из вершины и ее прямых потомков, которые являются листьями, называется кустом или веером.

Дерево вывода цепочки a+a * a в грамматике G₀ показано на рис 6.2 (а). Самый левый куст состоит из самой левой вершины, помеченной F, которая является его корнем, и кроны a.

Если удалить единственный лист самого левого куста, то останется дерево, показанное на рис. 6.2 (б). Крона F+a * a этого дерева и есть результат левой свертки цепочки a+a * a, а его основа - крона F поддерева с корнем, помеченным T. Опять удалив основу, получим дерево на рис 6.2 (в).

Описанный процесс свертки деревьев называется отсечением основ.

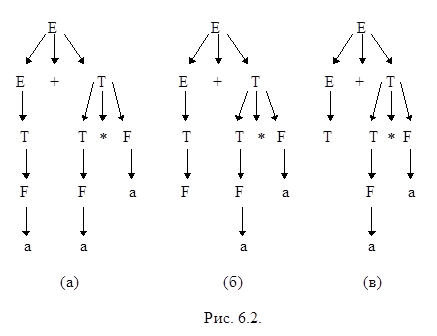
По КС-грамматике G можно построить эквивалентный расширенный МП-автомат R, работа которого заключается в отсечении основ. Здесь удобно представлять себе магазин в виде цепочки, верхним символом которой является самый правый, а не самый левый символ. В силу этого, отношение перехода ú¾ в этом автомате будет определятся несколько иначе. Если d (q, a, a) содержит (p, b), то будем писать

(q, aj, ga) ú¾ (p, j, gb)

для всех j Î S ^* и g Î G ^*.

В дальнейшем, если не оговорено противное, будем считать, что у обычного МП-автомата (нисходящего анализатора) верх магазина расположен слева, а у расширенного (восходящего анализатора) - справа.

Теорема 6.3. Пусть G=( N, S, P, S) - КС-грамматика. По G можно построить такой расширенный МП-автомат R, что L(R) = L(G).

Эта теорема является следствием теорем 6.1 и 6.2, но здесь интересна сама конструкция расширенного МП-автомата R, который и моделирует процесс отсечения основ. Итак

R = ({q, r}, S, N È S È {$}, d, q, $, {r})

- расширенный МП автомат, где по соглашению верх магазина расположен справа, и, в котором d определяется следующим образом:

(1) d (q, a, e) = {(q, a)} для всех aÎ S. (На этих тактах входные символы переносятся в магазин.)

(2) Если A ® a принадлежит P, то d (q, e, a) содержит (q, A). (В случае, когда в верхней части магазина окажется правая часть некоторой продукции эта правая часть может быть заменена левой частью соответствующего правила без движения по входной ленте.)

(3) d (q, e, $S) = {(r, e)}. (Если вся входная цепочка прочитана и в вершине магазина только начальный символ грамматики, автомат переходит в заключительную конфигурацию.)

Можно показать, что процесс вычисления в автомате R заключается в построении правовыводимых цепочек грамматики G, начиная с терминальной цепочки (на входе R) и кончая цепочкой S. 

Пример 6.5. Построим “восходящий” расширенный автомат R для грамматики арифметических выражений G₀ . Пусть R = ({q, r}, S, G, d, q, $, {r}), где d определяется так:

(1) d (q, b, e) = {(q, b)} для всех bÎ {a, +, *, (,)};

(2) d (q, e, E+T) = {(q, E)}

d (q, e, T) = {(q, E)}

d (q, e, T * F) = {(q, T)}

d (q, e, F) = {(q, T)}

d (q, e, (E)) = {(q, F)}

d (q, e, a) = {(q, F)};

(3) d (q, e, $E) = {(r, e)}.

Для входа a+a * a распознаватель может сделать следующую последовательность тактов:

(q, a+a * a, $) ú¾ (q, +a * a, $a)

ú¾ (q, +a * a, $F)

ú¾ (q, +a * a, $T)

ú¾ (q, +a * a, $E)

ú¾ (q, a * a, $E+)

ú¾ (q, * a, $E+a)

ú¾ (q, * a, $E+F)

ú¾ (q, * a, $E+T)

ú¾ (q, a, $E+T * )

ú¾ (q, e, $E+T * a)

ú¾ (q, e, $E+T * F)

ú¾ (q, e, $E+T)

ú¾ (q, e, $E)

ú¾ (r, e, e)

Заметим, что для входа a+a * a распознаватель R может сделать много различных последовательностей тактов. Однако представленная последовательность - единственная, которая переводит начальную конфигурацию в заключительную. €

Покажем теперь, что язык, определяемый МП-автоматом, контекстно-свободен.

Теорема 6.4. Пусть R = (Q, S, G, d, q₀ , Z₀ , F) - МП-автомат. Можно построить такую КС-грамматику G, что L(G) = L(R).

Доказательство. Построим G так, чтобы левый вывод цепочки w в грамматике G прямо соответствовал последовательности тактов, которую делает R при обработке цепочки w. Нетерминальные символы будут иметь вид < qZr>, где q, rÎ Q и ZÎ G.

Формально пусть G = (N, S, P, S), где

(1) N = {< qZr> ½ q, rÎ Q, ZÎ G }È {S};

(2) правила множества P строятся так:

(а) если d (q, a, Z) содержит (r, X₁ ... X_k) (k ³ 0), добавим к P все правила вида

< qZs_k > ® a< rX₁ s₁ ><s₁ X₂ s₂ >... <s_k-1 X_k s_k >

для каждой последовательности s₁ , s₂ ,..., s_k состояний из Q,

(б) если d (q, a, Z) содержит (r, e), добавим к P правило < qZr > ® a,

(в) добавим к P правила S ® < q₀ Z₀ q > для каждого qÎ Q.

Индукцией по m и n можно доказать, что для любых q, rÎ Q ZÎ G

< qZr> Þ ^m w тогда и только тогда, когда (q, w, Z) ú¾ ⁿ (r, e, e).

Из этого утверждения следует, что

S Þ < q₀ Z₀ q > Þ ⁺ w

тогда и только тогда, когда

(q₀ , w, Z₀) ú¾ ⁺ (r, e, e)

для qÎ Q. Таким образом L(R) = L(G). ›

Результаты данного раздела можно сформулировать в виде следующей теоремы:

Теорема 6.5. Утверждения

(1) L = L(G) для КС-грамматики G,

(2) L = L(R₁) для МП-автомата R₁,

(3) L = L(R₂) для расширенного МП-автомата R₂.

эквивалентны.

Доказательство. Из (2) следует (1) по теореме 6.4. Из (1) следует (2) по теореме 6.2. Из (3) следует (2) по теореме 6.1, а (3) тривиально следует из (2). ›

Дата добавления: 2015-06-27