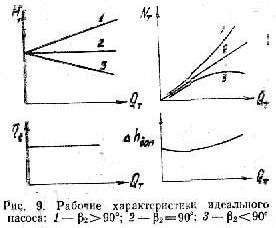
Рабочие характеристики идеального центробежного насоса

Рабочими характеристиками центробежного насоса называется совокупность зависимостей Н = f ₁(Q), h = f ₂(Q), N _эф = f ₃(Q),, D h _доп = f ₄(Q), найденных при постоянной частоте вращения рабочего колеса n.

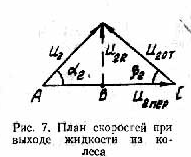
Для того чтобы найти связь Н _т и Q _т для идеального насоса, выразим в уравнении (12) u ₂cosa₂ через расход Q _т. Из треугольника скоростей (рис. 7), построенного для жидкости на периферийной части колеса, легко установить, что

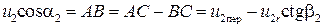, (13)

где u _2r – проекция u ₂ на радиальное направление; u _{2 отн} – скорость жидкости относительно лопаток колеса; b₂ – угол образуемый линией лопатки в месте се пересечения с внешней окружностью колеса, или угол между u ₂ и u _2пер = w r ₂ – скорость переносного движения, или окружная скорость вращения колеса.

Расход жидкости через колесо можно записать в виде

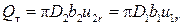(14)

где b _{2_} ширина проточной части колеса при диаметре D ₂.Подставим уравнение (13) и (14) в зависимость (12), найдем

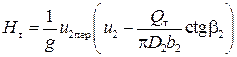. (15)

Уравнение (10) с учетом выражения (15):

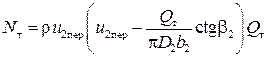(16)

КПД теоретического насоса h_т = 1 (17)

Уравнения (15)÷(17) и представляют собой характерис­тики идеального центробежного насоса.

В соответствии с решением, приведенным, в [3], кавитационный запас ∆ h _доп для идеального центробежного насоса, в котором гидравлические потери отсутствуют (x=0), можно рассчитать по формуле

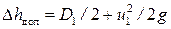
С учетом плана скоростей, построенного по условиям входа жидкости в межлопаточный канал (рис. 8),

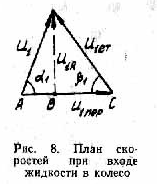
установим связь скорости u ₁ c u _1пер =π D ₁ n и u_{1 r} = Q _т/π D ₁ b ₁, где b ₁ — ширина проточной части колеса при диаметре D ₁. Поскольку

АВ = АС – ВС = u _1пер – u _{1 r} ctg b₁,

то нетрудно найти, что

,

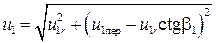а уравнение (18) легко привести к виду

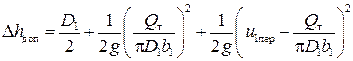(20)

В графическом виде рабочие характеристики идеального насоса приведены на рис. 9. Из рисунка видно, что в зна­чительной мере вид зависимостей H _T = f ₁(Q _T) и N _T = f ₃(Q _T)

определяется углом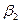

Выбор оптимальных углов b₁ и b₂

Анализ выполним для идеального насоса.

Центробежный насос проектируется для перекачивания жидкости в количестве Q _опт.

При известном значении Q _опт. угол b₁выбирается так, чтобы обеспечить условие безударного входа жидкости на лопатки, т. е. равенство скоростей до и после входа жидкости на лопасти.

Из условия a = 90° (см. рис. 8) и u ₁= u _{1 r} найдем

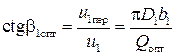_{. (21)}

При таком угле b₁ в реальном насосе гидравлические потери при входе жидкости в колесо будут минимальными.

Оптимальное значение угла b₂ найдем из условия получения в насосе максимума статической доли напора Н _ст в общей величине Н _т. Такая формулировка задачи правомерна только для случая нагнетания реальной жидкости, так как последующее преобразование динамического напора Н _дин в статический в улитке корпуса насоса или в направляющем аппарате (см. рис. 3) всегда связано с гидравлическими потерями и снижением КПД насоса.

Динамический напор, создаваемый насосом, вычислим по формуле

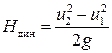(22)

Разложим скорости u ₂ и u ₁ на радиальные u _{2 r} и u_{1 r} и тангенциальные u _2t и u _1t составляющие:

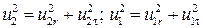
При оптимальном угле β₁ и _1t=0 и _.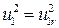

При конструировании межлопаточного канала колеса обычно выбирают профиль его таким, чтобы составляющая u_r оставалась постоянной величиной, т. е. и _{1 r}= u _{2 r}.

С учетом отмеченных особенностей уравнение (22) примет вид

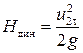(23)

С учетом выражений (13), (14) и соотношения u _2t= u ₂cosa₂ получим

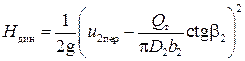
Статическая составляющая напора может быть найдена из уравнения

H_СТ = H_T - H_ДИН

или с учетом выражений (15) и (24)

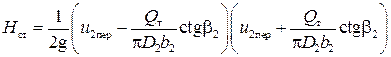(25)

На рис. 10 показаны зависимости H_Т = f₁(β₂) и H_CT = f₂(β₂)

Очевидно, что высокие напоры при β→π получаются за счет возрастания динамического напора. При уменьшении β₂ доля -статического напора возрастает. Из выражений (15) и (25) найдем

,

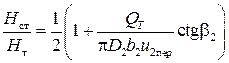При β₂ = π/2 H_CT/H_T= 1/2

при 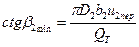, H_CT/H_T =1,но при этом как статический, так и полный напоры равны нулю. В реальных -насосах угол β₂ всегда принимают меньше 90°, но выше β_{2 min}. Обычно β₂=15÷35°.

Дата добавления: 2015-07-02