Формулы пропорциональности

Эти формулы отражают характер изменения основных параметров работы насоса (Q, Н, N _эф)при изменении частоты вращения n при условии сохранения гидродинамического подобия течения жидкости внутри рабочего колеса. т. е. при η = const. Это условие эквивалентно сохранение значения Q и H при изменении п.

Если насос при частоте n имеет параметры Q, Н и N _эф , а при n₁ – Q₁, H₁ и N_эф1, то с учетом выражений (30) и (31) можно записать

или

или

Поскольку и

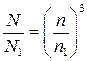
Очевидно, что формулы пропорциональности (32) — (34) справедливы лишь в узком диапазоне изменения n, так как е изменением n изменяются численные значения скоростей течения жидкости, а следовательно и число Rе, т. е. нарушается условие гидродинамического подобия.

При практических расчетах можно пользоваться формулами пропорциональности в области 0,8< n / n ₁< 1,25.

Если исключить из выражения (32) и (33) отношение n/n₁ то получим уравнение

H = (H₁/Q₁²)Q²,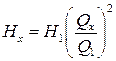

которое называется параболой подобных режимов, так как показывает характер зависимости Н от Q с изменением часоты вращения n при условии η =const.

Работа насоса на сеть. Способы регулированияпроизводительности насоса

Для нахождения параметров Q_A и Н_А, устанавливающихся при работе насоса на сеть, необходимо совместно решить уравнения характеристик насоса Н_Н=f₁(Q) и сети H_с = f₂(Q). Поскольку характеристика насоса задается в графической форме, то и решение задачи удобно искать, графически (рис. 18). Точка пересечения характеристик (т. е. решение задачи) называется рабочей точкой. Маловероятно, чтобы параметр Q_A совпал со значением производительности Q_c,требуемой технологией производства.

Для смещения рабочей точки можно либо изменить характеристику насоса так, чтобы она прошла через точку С на характеристике сети с параметрами Q_c, Н_с, либо воздействовать на характеристику сети.

Рассмотрим различные способы регулирования производительности насоса.

1. Способ дросселирования осуществляется путем установки дросселя (регулирующего вентиля или задвижки) в сети за насосом, т. е. на линии нагнетания (рис. 19). Установка дросселя перед насосом недопустима, так как ведет к понижению давления в насосе и тем самым способствует возникновению кавитации в нем. При этом спо-

собе регулирования очевидно, что расходы жидкости в насосе Q_н и в сети Q_с одинаковы, т. е. Q_н =Q_с (рис. 20). Поэтому насос имеет параметры точки А.

Вычислим КПД системы регулирования η_др при дросселировании:

2. Способ байпассирования осуществляется путем сброса части жидкости Q_б из линии нагнетания в линию всасывания через байпассную линию (рис. 21). При этом способе регулирования H_н=H_с т. е. насос имеет параметры точки В (рис. 22)...

Вычислим КПД системы регулирования η_б при байпассировании:

Очевидно, что в каждом конкретном случае лучшим из двух рассмотренных будет тот, который имеет больший КПД. Выбор способа регулирования зависит от крутизны характеристики насоса и положения точки С на характеристике сети.

Установим ориентировочное правило выбора. Если принять, что в первом приближении η_нне зависит от Q, то преимущество того или иного способа определяется отношениями Q_с/Q_н и Н_с/Н_н.

Если Q _с/ Q _н > Н _с/ Н _н, то выгоднее применять способ байпассирования. Это неравенство можно записать в виде

или tgα>tgβ, или α>β.

Геометрический смысл углов α и β ясен из рис. 23.

Таким образом, способ байпассирования следует применять при относительно крутых характеристиках насоса.

По аналогии можно показать, что способ дросселирования следует применять при α<β т. е. при относительно пологих характеристиках насоса.

3. При изменении частоты вращения рабочего колеса п и сохранении подобия режимов работы

одновременно изменяются напор и производительность насоса в соответствии с уравнениями (32) и (33), и, следовательно, можно изменить положение характеристики насоса, обеспечив прохождение ее через заданную точку С

Пусть характеристика насоса задана при частоте n₁(рис. 24). Найдем частоту п₁ при которой характеристика

Н_н=f(Q) пройдет через точку С. Для этого построим параболу подобных режимов (см. уравнение 35)

H = (Q/Q_c)²H_c,

точка пересечения которой с кривой зависимости Н_н=f(Q) даст точку А. Частоту п найдем по одной из формул пропорциональности:

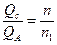или .

КПД насоса при работе его на сеть в точке С найдем по Q_А, так как в точках С и А режимы работы насоса подобны, а следовательно, КПД одинаковы.

Дата добавления: 2015-07-02