Гипотеза о независимости двух признаков

Пусть А и В - случайные признаки объектов ГС, 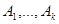и 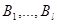- разбиения ГС на непересекающиеся классы по признакам А и В соответственно, k, l > 1.

Пример. А - цвет глаз, В - цвет волос студента.

Для произвольного объекта х ГС обозначим:

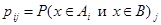- вероятность одновременной принадлежности х классам и

;

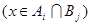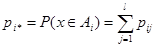- вероятность принадлежности х классу ;

- вероятность принадлежности х классу .

Эти неизвестные вероятности составляют теоретическую таблицу сопряжённости признаков

(ТСП)

Гипотеза 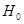о независимости признаков А и В:

Для любых i = 1, …, l (теорема умножения вероятностей для независимых событий).

Проверка гипотезы 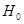о независимости признаков по - критерию.

1. Предварительная обработка выборки - составление эмпирической ТСП.

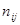- число элементов выборки, принадлежащих одновременно классам и ,

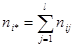- число элементов выборки, принадлежащих классу ,

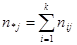- число элементов выборки, принадлежащих классу .

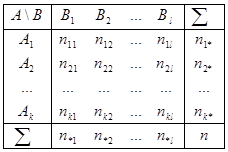
2. Основа статистики критерия – оценки неизвестных 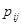по выборке

При верно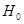й . - оценки 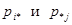по выборке, поэтому 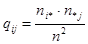- оценка 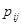при верной .

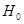Теперь 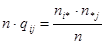- ожидаемое при верной 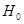количество элементов выборки, лежащих одновременно в и . Статистика критерия сравнивает эту величину с её эмпирическим значением .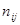

Статистика критерия

(1)

при верной 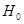и больших n (n ≥ 30), k, l имеет распределение с (k – 1)(l – 1) степенями свободы..

3. По данному УЗ α и числу (k – 1)(l – 1) степеней свободы по таблице критических значений статистики находится .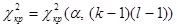

4.Выборочное значение статистики критерия легче вычислять по эквивалентной (1) формуле .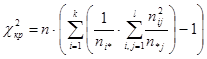

Если 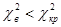, то 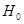принимается.

Если 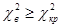, то 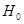отклоняется.

5. При отклонённой 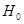степень зависимости признаков А и В оценивается коэффициентом сопряжённости признаков , где m = min { k, l }.

.

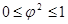Пример. (скопировать)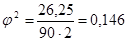

Дата добавления: 2015-07-02