Нормальное распределение силы тяжести Земли

НФ

НФ

НФ

Сначала, как всегда, формальное определение.

Схема отношения R находится в 1НФ, если значения в dom(A) являются атомарными для каждого атрибута A в R.

Другими словами, каждый атрибут отношения должен хранить одно-единственное значение и не являться ни списком, ни множеством значений.

Следует заметить, что, несмотря на внешнюю строгость данного определения, однозначно определить понятие атомарности зачастую оказывается довольно затруднительно, если заранее неизвестны семантика атрибута и его роль в обработке хранимых данных. Атрибут, который является атомарным в одном приложении, может оказаться составным в другом.

Простейший пример: в БД отдела кадров предприятия в таблице, хранящей личные сведения о сотрудниках, имеется атрибут "домашний-адрес", в котором адрес хранится в формате: город, улица, дом[/корпус], [квартира] (следуя общепринятой нотации, здесь в квадратных скобках указаны опциональные фрагменты адреса, которые могут отсутствовать). В данном случае адрес хранится в виде единой текстовой строки, поскольку маловероятно, чтобы потребовалось выбрать сотрудников, скажем, по номеру квартиры. Таким образом, в контексте БД отдела кадров адрес является атомарным понятием, и его деление на составные части не имеет смысла, т.к. только внесет в БД излишнюю громоздкость.

Однако тот же адрес для приложения, предназначенного для сортировки почты в почтовом отделении, атомарным не является, поскольку желательно сгруппировать конверты в отдельные стопки по улицам, так как каждую улицу обслуживает свой почтальон. Кроме того, с целью оптимизации перемещений почтальона в пределах улицы, каждую стопку желательно отсортировать по номерам домов, чтобы сделать возможным разнести почту за один проход по улице без возврата.

Итак, очевидно, что в отрыве от контекста затруднительно дать строгое определение атомарности, за исключением самых простых случаев (например, домен натуральных чисел). В большинстве случаев необходимо располагать сведениями о предметной области, а также о том, каким образом планируется обрабатывать хранимые в БД данные.

Приведение отношения к 1НФ - довольно простая операция. Мы должны просмотреть схему отношения и разделить составные атрибуты на различные строки/столбцы. Возможно, эту операцию придется повторить несколько раз до тех пор, пока каждый из атрибутов не станет атомарным (с учетом сказанного в предыдущем абзаце).

Приведу небольшой пример. (Этот пример, как и остальные в данной статье, любезно предоставила мне Never, за что я ей сердечно благодарен, поскольку это позволило мне сэкономить массу времени и избежать выдумывания достаточно правдоподобных примеров).

В БД имеется таблица контрагентов, в которой хранятся следующие сведения:

наименование агента;

город;

адрес;

электронный адрес;

веб-страница;

вид агента (поставщик или клиент);

контактные лица (может быть несколько), должность контактного лица, телефон контактного лица.

Табл. 2

Наим.	Город	Адрес	Эл. почта	WWW	Вид	Конт. лица
Поршневой з-д	Владимир	Ул. 2-я Кольцевая, 17	[email protected]	www.plunger.ru	Поставщик	Иванов И.И., зам. дир., тел [phone] Петров П.П., нач. отд. сбыта, тел [phone]
ООО Вымпел	Курск	Ул. Гоголя, 25	[email protected]		Клиент	Сидоров С.С., директор, тел. [phone]
ИЧП Альфа	Владимир	Ул. Пушкинская, 37, оф. 565	[email protected]		Клиент	Васильев В.В., директор, тел [phone]

Очевидно, что в данном случае атрибут "конт-лица" не является атомарным, поскольку в нем попадаются списки из нескольких лиц. Разделим эти кортежи таким образом, чтобы каждый кортеж содержал данные только об одном лице:
Табл.3

Наим.	Город	Адрес	Эл. почта	WWW	Вид	Конт. лица
Поршневой з-д	Владимир	Ул. 2-я Кольцевая, 17	[email protected]	www.plunger.ru	Поставщик	Иванов И.И., зам. дир., тел [phone]
Поршневой з-д	Владимир	Ул. 2-я Кольцевая, 17	[email protected]	www.plunger.ru	Поставщик	Петров П.П., нач. отд. сбыта, тел [phone]
ООО Вымпел	Курск	Ул. Гоголя, 25	[email protected]		Клиент	Сидоров С.С., директор, тел. [phone]
ИЧП Альфа	Владимир	Ул. Пушкинская, 37, оф. 565	[email protected]		Клиент	Васильев В.В., директор, тел [phone]

Несколько лучше, хотя при ближайшем рассмотрении оказывается, что атрибут "конт-лица" снова может быть назван атомарным лишь с натяжкой, поскольку содержит разнородные данные, хотя и об одном лице.

Разобьем его на несколько атрибутов:

Табл. 4

Наим.	Город	Адрес	Эл. почта	WWW	Вид	Должность	Ф.И.О.	Код города	Тел.
Поршневой з-д	Владимир	Ул. 2-я Кольцевая, 17	[email protected]	www.pler.ru	Поставщик	зам. дир.	Иванов И.И.		76-1595
Поршневой з-д	Владимир	Ул. 2-я Кольцевая, 17	[email protected]	www.pler.ru	Поставщик	нач. отд. сбыта	Петров П.П.,		7615-35
ООО Вымпел	Курск	Ул. Гоголя, 25	[email protected]		Клиент	директор	Сидоров С.С.		6665-38
ИЧП Альфа	Владимир	Ул. Пушкинская, 37, оф. 565	[email protected]		Клиент	директор	Васильев В.В.

Теперь можем считать, что каждое значение каждого из атрибутов нашего отношения является атомарным. Следовательно, отношение находится в 1НФ.

Теперь наше отношение выглядит несколько корректнее. Однако даже беглый взгляд на него говорит о том, что оно пока еще далеко от совершенства. Очевидно, что повторяющиеся значения, которых немало в предыдущей таблице, являются потенциальным источником проблем.

Во-первых, при вводе их значений легко ошибиться. Например, достаточно изменить всего одну букву в графе "Адрес", и формально это будет уже совершенно другой адрес, не имеющий ничего общего с первым. Найти подобные опечатки в объемной таблице - задача не из простых.

Во-вторых, название улицы может измениться, хоть это происходит и не так часто (тем не менее пренебрегать такой возможностью не стоит). Может измениться и адрес веб-сайта предприятия, что гораздо вероятнее. Тогда придется опять же шерстить всю таблицу и изменять соответствующие значения.

В-третьих, нельзя пренебрегать и эффективностью хранения информации. Из нашей таблицы можно как минимум дважды узнать адрес поршневого завода, хотя нам хватило бы и одного раза. В данном примере это мелочи, но на практике встречаются базы пообъемнее. Например, лично мне приходится иметь дело с таблицами, которые за месяц подрастают до нескольких сотен миллионов записей. Как нетрудно прикинуть, лишнее поле размером всего-навсего в 10 байт раздует объем файла, в котором физически размещена таблица, на несколько гигабайт. Помимо того, что эти гигабайты нужно хранить на диске, при операциях с базой их приходится прокачивать из дисковой памяти в оперативную, а порой и в локальную сеть.

Таким образом, борьба с избыточностью данных выгодна со всех сторон - как со стороны повышения удобства пользования данными и поддержания их в целостном виде, так и со стороны эффективности обработки и хранения данных аппаратными средствами сервера баз данных. Именно на устранение этой избыточности и направлена дальнейшая нормализация отношений.

Однако перед тем, как дать определение 2НФ, нам необходимо познакомиться с понятием полной и частичной функциональной зависимостей. По традиции сначала - формальное определение.

Пусть F - множество функциональных зависимостей, при этом ФЗ X->Y F+. Множество Y называется частично зависимым от X относительно F, если ФЗ X->Y не является редуцированной слева (т.е. существует собственное подмножество X множества X, такое, что ФЗ X'->Y F+. Если же ФЗ X->Y является редуцированной слева, то множество Y называется полностью зависимым от X относительно F.

Схема отношения R находится во 2НФ относительно множества функциональных зависимостей F, если она находится в 1НФ и каждый неключевой атрибут полностью зависит от каждого ключа для R.

Теперь для тех, кто предпочитает неформальные определения, попытаюсь дать интуитивно понятный аналог вышесказанного. Другими словами, отношение находится во 2НФ, если оно находится в 1НФ, и при этом все неключевые атрибуты зависят только от ключа целиком, а не от какой-то его части.

Вернемся к нашей табл. 4, которая представляет пример нашего отношения, приведенного к 1НФ. Предположим, что при постановке задачи заказчик сообщил нам, что в пределах каждого города наименование предприятия является уникальным, но в разных городах названия могут совпадать. Таким образом, предприятие характеризуется составным ключом "Наим+Город". Посмотрим на наше отношение с точки зрения того, что мы только что узнали про 2НФ.

Очевидно, что телефонный код города зависит исключительно от самого города и никак не связан с названием предприятия. Отсюда и один из источников избыточных данных - сколько раз в таблице встречается строка, содержащая сведения о контактном лице какого-либо предприятия, находящегося в данном городе, столько раз и повторяется информация о коде города.

Чтобы устранить эту избыточность, нам придется разбить наше отношение на несколько (в данном случае - 2, хотя для более сложных отношений их может быть и гораздо больше):

Табл. 5а

Наим.	Город	Адрес	Эл. почта	WWW	Вид	Должность	Ф.И.О.	Тел.
Поршневой з-д	Владимир	Ул. 2-я Кольцевая, 17	[email protected]	www.plunger.ru	Поставщик	зам. дир.	Иванов И.И.	76-15-95
Поршневой з-д	Владимир	Ул. 2-я Кольцевая, 17	[email protected]	www.plunger.ru	Поставщик	нач. отд. сбыта	Петров П.П.,	76-15-35
ООО Вымпел	Курск	Ул. Гоголя, 25	[email protected]		Клиент	директор	Сидоров С.С.	66-65-38
ИЧП Альфа	Владимир	Ул. Пушкинская, 37, оф. 565	[email protected]		Клиент	директор	Васильев В.В.	74-57-45

Табл. 5б

Город	Код города
Владимир
Курск

Итак, мы избавились от частичной зависимости атрибута "Код-города" от составного ключа, переместив коды городов в отдельное отношение с ключом "Город". Таким образом, теперь мы получили два отношения, каждое из которых находится во 2НФ.

Следует обратить внимание на факт, который далеко не всегда явно отражен в литературе по базам данных. Поскольку в данном случае речь идет о частичной зависимости атрибутов от ключа, то все вышесказанное относится исключительно к отношениям с составным ключом. Отношение с простым, или атомарным, ключом (состоящим из единственного атрибута), приведенное к 1НФ, находится во 2НФ по определению и в данном этапе нормализации не нуждается.

Несмотря на предпринятые усилия, таблица 5а определенно все еще содержит изрядную избыточность - достаточно взглянуть на повторяющиеся значения в столбцах "Адрес", "Эл.почта" и "WWW". Значит, процесс нормализации еще не завершен, и пора переходить к его следующей стадии.

Для того, чтобы формально определить 3НФ, нам придется предварительно познакомиться с понятием транзитивной зависимости атрибутов, от которой мы попытаемся избавиться на этом этапе.

Обозначим: R - схема отношения, X - подмножество R, A - атрибут в R, F - множество функциональных зависимостей. A называется транзитивно зависимым от X в R, если существует такое Y, являющееся подмножеством R, что:

X->Y

~(Y->X)

Y->A

~(A XY)

Теперь можно дать собственно определение 3НФ:

Схема отношения R находится в 3НФ относительно множества функциональных зависимостей F, если она находится в 1НФ и ни один из непервичных атрибутов в R не является транзитивно зависимым от ключа для R.

Вольное изложение определения: чтобы привести отношение к 3НФ, необходимо устранить функциональные зависимости между неключевыми атрибутами отношения. Другими словами, факты, хранимые в таблице, должны зависеть только от ключа.

В реляционной теории имеется лемма, которая гласит, что любая схема отношения, находящаяся в 3НФ относительно F, находится в 2НФ относительно F.

В нашем случае присутствует функциональная зависимость между атрибутами "Ф.И.О.", "Должность" и "Тел." Очевидно, что на предприятии некий человек занимает определенную должность и располагает определенным рабочим телефоном. Обратное в общем случае неверно - на предприятии может быть несколько аналогичных штатных единиц, например, менеджеры по сбыту, и несколько человек могут пользоваться одним рабочим телефоном.

Чтобы избавиться от данной функциональной зависимости,, проведем декомпозицию таблицы 5а на две таблицы.

Первая из них хранит факты, относящиеся непосредственно к самому предприятию:

Табл. 6а

Наим.	Город	Адрес	Эл. почта	WWW	Вид
Поршневой з-д	Владимир	Ул. 2-я Кольцевая, 17	[email protected]	www.plunger.ru	Поставщик
ООО Вымпел	Курск	Ул. Гоголя, 25	[email protected]		Клиент
ИЧП Альфа	Владимир	Ул. Пушкинская, 37, оф. 565	[email protected]		Клиент

Вторая таблица хранит факты, относящиеся к конкретному лицу, исполняющему некоторые обязанности на данном предприятии:

Табл. 6б

Наим.	Город	Ф.И.О.	Должность	Тел.
Поршневой з-д	Владимир	Иванов И.И.	зам. дир.	76-15-95
Поршневой з-д	Владимир	Петров П.П.,	нач. отд. сбыта	76-15-35
ООО Вымпел	Курск	Сидоров С.С.	директор	66-65-38
ИЧП Альфа	Владимир	Васильев В.В.	директор	74-57-45

Вместе с таблицей 5б данный набор таблиц представляет собой нашу исходную базу данных, приведенную к 3НФ.

В 1743 году французский ученый Клеро разработал теорию зависимости между ГПЗ и фигурой Земли. Исходя из закона всемирного тяготения, Клеро получил математические соотношения, связывающие форму Земли с распределением на ней силы тяжести. Эти соотношения имеют вид:

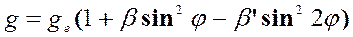(6)

где ;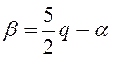

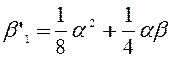
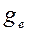- ускорение силы тяжести на экваторе;

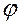- широта точки земной поверхности;

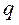- отношение максимального значения центробежного ускорения к минимальному значению ускорения силы тяжести,

;

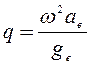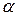- сжатие, (а и b - большая и малая полуоси земного эллипсоида).

В последней формуле 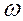- угловая скорость вращения Земли, рад/с (в знаменателе стоит число средних секунд в звездных сутках), 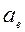- большая полуось Земли, 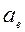=6378137 м; 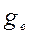- значение силы тяжести на экваторе, 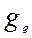=978,03 Гал,

При указанных значениях .

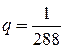Формула (6) характеризует поле силы тяжести некоторой осредненной Земли, представленной в виде эллипсоида вращения.

Подбором параметров можно добиться наилучшего приближения модели гравитационного поля, представляемого формулой (6), к реальному полю Земли вблизи ее поверхности. Формула (6) с численными коэффициентами, представляющими эту модель, называется формулой нормального распределения силы тяжести.

Для подбора численных значений параметров необходимо замерять величину q, в большом числе точек, равномерно распределенных по земной поверхности, подставлять найденные значения в формулу (6) и решить систему уравнений (6) относительно искомых параметров с обработкой результатов методом наименьших квадратов.

Введение модели нормального гравитационного поля, например, в виде (6), позволяет заменить поле силы тяжести реальном Земли более простым разностным полем аномалий силы тяжести, образованных как разность истинного и нормального полей. Аномалии намного меньше нормальной составляющей силы тяжести, и операций с ними значительно проще.

Система аномалий зависит от того, какая модель нормального поля принята за основу. Введение новой модели влечет за собой большую работу по перевычислению аномалий. Поэтому, хотя было предложено много формул нормальной силы тяжести, практически до последнего времени применялись формула Гельмерта (1901 - 1909 гг.), имеющая вид:

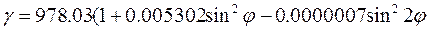(7)

и соответствующая эллипсоиду со сжатием α=1:298,2 и формула Каcсиниса (1930 г.), получившая также название международной, имеющая вид:

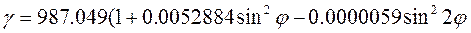Гал (8)

и соответствующая эллипсоиду со сжатием α =1:297,0. Формула Гельмерта получена по небольшому числу гравиметрических измерений. При ее выводе использовано лишь 1603 осредненных значения ускорения силы тяжести. Коэффициенты g_e и β найдены путем решения системы уравнений вида (6). Коэффициент β’ вычислен теоретически, на основе гипотезы Дарвина и Вихерта о внутреннем строении Земли.

При выводе формулы Кассиниса использовались геодезические и гравиметрические методы. В ней в качестве сжатия α принято значение сжатия международного геодезического эллипсоида относимости 1930 г., и по нему вычислены параметры β и β', только экваториальная постоянная g_e получена гравиметрическим путем.

Дата добавления: 2015-07-02