Нормальное распределение

Непрерывная случайная величина X имеет нормальное распределение, если ее плотность распределения вероятности имеет вид:

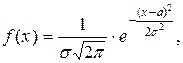
где и – параметры распределения, причем = M (X), = (X).

График дифференциальной функции распределения называют нормальной кривой, или кривой Гаусса (рис.1).

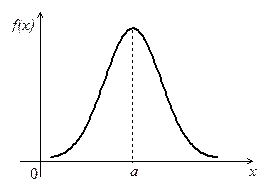
Рис.1

Если 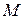(X) = 0, 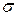(X) = 1, то нормально распределенная случайная величина называется нормированной, ее дифференциальная функция распределения 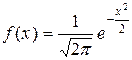табулирована.

Вероятность попадания нормально распределенной случайной величины в интервал (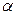, 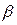) находим по формуле:

Данный интеграл выражается через функцию Лапласа, которую еще называют интегралом вероятностей и обозначают Ф (t):

Ф (t) .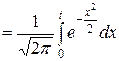

Функция Лапласа – это вероятность попадания нормированной нормально распределенной случайной величины в интервал (0, t).

Функция Лапласа обладает следующими свойствами:

1. Ф (0) = 0.

2. Ф (– t) = – Ф (t), то есть она нечетная.

3. Ф (¥) = 0,5 (практически уже при t > 4).

Функция Ф (t) табулирована (см. прил. 2).

Применяя функцию Лапласа, получим:

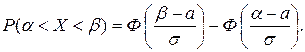
При решении задач часто возникает необходимость определения вероятности отклонения нормально распределенной случайной величины от ее математического ожидания:

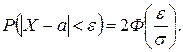
Пример 1. Средний процент выполнения плана некоторыми предприятиями составляет 105 %, среднее квадратическое отклонение – 5 %. Полагая, что выполнение плана предприятиями подчинено закону нормального распределения, вычислить долю предприятий, выполняющих план от 110 до 130 %, то есть определить вероятность попадания рассматриваемой величины в интервал (110, 130).

Решение. Случайная величина X – выполнение плана предприятиями; она имеет нормальное распределение с параметрами:

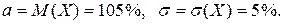Для нахождения искомой вероятности воспользуемся формулой:

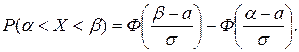
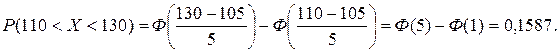
Пример 2. Длина изготовляемой детали представляет собой случайную величину, распределенную по нормальному закону. Средняя длина детали равна 50 мм, а дисперсия – 0,25 мм². Какое поле допуска длины изготовляемой детали можно гарантировать с вероятностью 0,99?

Решение. Длина изготовляемой детали – случайная величина X, имеющая нормальный закон распределения с параметрами:

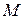= (X) = 50 мм, 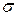= 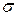(X) = 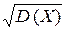= 0,5.

Известна вероятность, гарантирующая некоторое поле допуска, то есть Р (a< X < b) = 0,99. Чтобы найти это поле допуска, воспользуемся формулой:

Неравенство ½ X – ½< e эквивалентно неравенству , следовательно, и равновероятно, то есть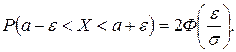

Исходя из условия задачи, можем записать:

= 0,99; 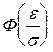= 0,495.

По таблице значений функции Лапласа (см. прил. 2) находим 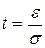= 2,58.

Отсюда e = 2,58 × 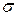= 1,29, тогда 50 – 1,29 £ X £ 50 + 1,2 или 48,71 £ X £ 51,29.

Дата добавления: 2015-07-02