Основные понятия и определения. Термодинамика, как наука о преобразованиях энергии, исследует процессы, происходящие в системах, состоящих из взаимодействующих материальных тел

ВВЕДЕНИЕ

Термодинамика, как наука о преобразованиях энергии, исследует процессы, происходящие в системах, состоящих из взаимодействующих материальных тел.

Главным назначением технической термодинамики является применение физических законов природы для совершенствования и создания новых высокоэффективных теплоэнергетических установок, двигателей и аппаратов. Теоретическими основами для этого являются закон сохранения и превращения энергии (первый закон термодинамики) и закон определенной направленности процессов преобразования энергии (второй закон термодинамики).

Согласно первому закону энергия не исчезает и не рождается, она только превращается из одного вида в другой. При этом, какое количество одного вида энергии израсходовано - точно такое же количество энергии других видов обязательно будет получено. Так, для материальных систем, не допускающих утечку массы, а только передачу энергии от одной системы к другой, всегда справедливо равенство

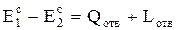, (0.1)

где 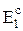и 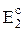- полная энергия системы в начале и в конце процесса отдачи энергии в форме теплоты Q_отв и в форме работы L_отв.

Для адиабатных процессов

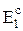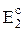- = L_отв. (0.2)

Для систем, в которых имеется «утечка» массы, математическим выражением первого закона термодинамики будет равенство

, (0.3)

где E_ут - энергия массы вещества в процессе утечки этой массы. Обычно E_ут представляет энтальпию вытекающего вещества.

Согласно второму закону полезная работа может быть получена только в условиях, когда могут совершаться естественные процессы изменения состояний рабочих тел и источников теплоты. При этом в конечном итоге часть высокопотенциальной энергии системы (в том числе - направленного движения) превращается в низкопотенциальную энергию и в форме теплоты отводится в окружающую среду. В технической термодинамике рассматриваются теплоэнергетические системы, состоящие не только из источников теплоты (теплоотдатчиков, теплоприемников) и рабочих

тел, но и окружающей среды. В качестве окружающей среды принимается обычно вода в открытых водоемах (для паровых установок) или охлаждающий воздух. И хотя во времени параметры окружающей среды Р_ос и Т_ос изменяются, для процессов работы системы они являются независимыми. К тому же такую окружающую среду можно считать бесконечно емкой, а ее давление P_oc и температуру T_oc при любом количестве подведенной или отведенной теплоты (Q_oc) принимать неизменными. При термодинамическом равновесии рабочего тела с окружающей средой обязательно сохраняется равенство их давлений (P_{o =} P_oc) и температур (T_{o =} T_oc). Все их экстенсивные параметры (U, H, V, S) будут различными.

При анализе любых процессов в теплоэнергетической системе следует обязательно учитывать естественную направленность всех ее процессов, подчиненных второму закону термодинамики.

Так, согласно формулировке второго начала, предложенной P. Клаузиусом, «…теплота не может переходить сама собой от тела более холодного к телу более нагретому». Для такого перехода нужно, чтобы в системе происходил где-то переход теплоты от тела более нагретого - к холодному, где теплота может переходить «сама собой». При таком естественном переходе в соответствующих системах можно выработать полезную работу. Для осуществления противоестественных процессов надо затратить определенную работу или теплоту горячего источника. Нужно также помнить формулировку, предложенную М. Планком, о невозможности осуществления вечного двигателя второго рода, т.е. двигателя, который бы полностью превращал в работу всю теплоту, отводимую от горячего источника.

Для работы теплового двигателя нужно иметь два источника теплоты - горячий и холодный. К последнему должна отводиться определенная часть теплоты горячего источника. Из этой формулировки следует, что отводимая от горячего тела теплота, в отличие от других видов энергии, никогда не может полностью превратиться в работу. Это положение вытекает из самой сущности тепловой энергии, как энергии хаотического молекулярного движения, которая, естественно, не может превратиться полностью в энергию направленного движения. В отличие от теплоты, все другие виды энергии, рассматриваемые в технической термодинамике, полностью превратимы в работу.

Важнейшим следствием второго закона термодинамики во всех реальных процессах, совершаемых в природе, как естественным путем, так и принудительно, является обязательное превращение части энергии направленного движения в теплоту диссипации. Это происходит в результате необходимости преодоления механического, гидравлического или термического сопротивлений. Даже в тех случаях, когда израсходованная на преодоление таких сопротивлений работа снова возвращается к этому же телу в форме теплоты, последнюю уже невозможно полностью превратить снова в работу. Происходит как бы обесценивание энергии или потеря ее качества (с точки зрения возможности производства работы). В этом суть необратимости реальных процессов.

На основании вышеизложенного, в соответствии с первым и вторым законами термодинамики, для всех реальных технических процессов уравнение (0.1) может быть записано в виде

(0.4)

где DQ_дис = DL_пот; 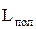- отведенная от системы полезная работа. Сумма представляет располагаемую работу системы.

Так, для какого-либо тела, изменяющего в исследуемом процессе свою внутреннюю энергию от U₁ до U₂ и совершающего работу расширения L = 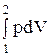, уравнение (0.4) после его дифференцирования примет вид

dQ_под + dQ_дис = dU + pdV. (0.5)

Полученное уравнение относится к разряду голономных, которое путем деления на интегрирующий делитель превращается в уравнение полных дифференциалов. Таким делителем является абсолютная температура Т, что доказывается математически.

На этом основании из (0.4) получаем объединенное уравнение первого и второго законов термодинамики для рассматриваемых систем

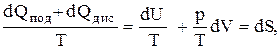(0.6)

где S - экстенсивный параметр состояния данного тела или системы, приращение dS которого является полным дифференциалом. Этот параметр, как известно, называется энтропией. Отсюда приращение энтропии любой термодинамической системы составит

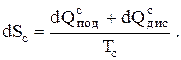(0.7)

Соответственно, для адиабатных технических систем, состоящих из горячих источников, рабочих тел и бесконечно емкой окружающей среды (с независимыми параметрами P₀ , T₀), получим

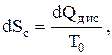
откуда с учетом (0.4) находим

dQ_дис = dL_пот = T₀ dS_c, (0.8)

где T₀ = const.

При этом суммарные потери возможной работы в системе, вызванные диссипацией ее энергии, можно рассчитать по формуле

L_пот = Q_дис = T₀ DS_c, (0.9)

где DS_c представляет собой алгебраическую сумму приращений энтропии всех составных частей системы

DS_c = DS_гор + DS_рт + DS_ос. (0.10)

Используя уравнения (0.1), (0.2) и (0.9), можно определить максимально возможную работу любой теплоэнергетической системы. Для этого все процессы должны быть обратимыми, а DQ_дис = DL_пот = 0.

Отсюда, согласно (0.10), должно быть

DS_гор + DS_рт + DS_ос = 0. (0.11)

Сама величина максимальной работы системы найдется из уравнения

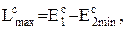(0.12)

где 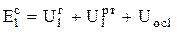- сумма внутренних энергий горячих источников, рабочих тел и окружающей среды до совершения работы; 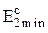- энергия системы после совершения максимальной работы при достижении ею термодинамического равновесия при p_c = p₀ и T_c = T₀.

В этом случае внутренняя энергия горячих источников становится равной 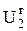, внутренняя энергия действия тел - U₀ и окружающей среды - .

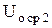При этом уравнение (0.12) получит вид

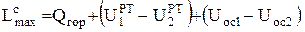. (0.13)

Для окружающей среды, которая может обратимо обмениваться энергией с рабочим телом в форме теплоты, отводимой при T₀, и работы, совершаемой при р = р₀, согласно (0.3) и с учетом (0.11) получим

U_{ос 1} - U_{ос 2} = p₀ (V₁ - V₀) - T₀ 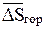- Т₀ (S₁ - S₀).

Подставляя это значение (U_{ос 1} - U_{ос 2}) в (0.13), получим

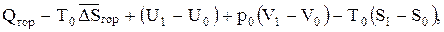(0.14)

где 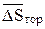- уменьшение энтропии горячих источников, вызванное отводом от них теплоты Q_гор.

Из (0.14) следует, что для технической системы (теплоэнергетической установки), в которой рабочее тело совершает заданный цикл и, следовательно, для которого U₁ = U₀, V₁ = V₀ и S₁ = S₀, максимальная работа составит

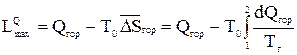. (0.15)

Величину 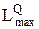называют «эксергией теплоты» и обозначают через Ex^Q.

Уравнение (0.15) справедливо для любых способов преобразования

теплоты, в том числе и для прямого ее преобразования в электроэнергию без всяких циклов. При переменном T_г из (0.15) находим

,

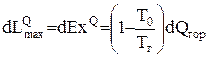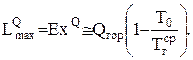(0.16)

Эксергия системы, производящей работу только за счет внутренней энергии рабочего тела (горячий источник отсутствует, а тело неподвижно), определяется по формуле

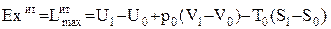. (0.17)

Произведение T₀S - часть внутренней энергии тела, которая в самом идеальном случае не может совершить работу. Эту часть энергии называют «анергией»

(0.18)

Эксергия технических систем, для которых рабочие тела находятся в непрерывном потоке, а их энергия состоит из суммы энтальпии и кинетической энергии потока (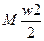), определяется по формуле

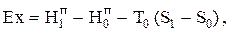(0.19)

где - энтальпия заторможенного потока.

Величину Ex называют технической эксергией, а термодинамическую функцию (H - T₀S) - эксергетическим потенциалом. Из приведенных формул видно, что энтропия является показателем непревратимости определенной части внутренней энергии в работу.

В этом ничего сверхъестественного нет, ибо, как видно из правой части уравнения (0.6), энтропия является только функцией таких реальных параметров состояния материальных тел, как давление, температура, удельный объем и внутренняя энергия. Она является таким же параметром состояния тела, как системы, состоящей из огромного числа микрочастиц, и характеризует равномерность их теплового хаотического движения. Чем больше энтропия, тем более равномерно распределено это хаотическое движение и тем меньшую работу оно может дать. Распространять понятия энтропии на системы, в которых нет хаотического движения большой массы частиц, неправомерно, поскольку такие системы не имеют ни давления, ни температуры.

Все вышеизложенное позволяет сформулировать следующие важнейшие положения.

1. Второй закон термодинамики не связан с циклами, он действует при любых способах производства работы за счет тепловой энергии. Максимальная работа любой термодинамической системы всегда определяется величиной ее эксергии.

2. Потери работы любой термодинамической системы от необратимости каких-либо процессов равны произведению 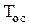на суммарное приращение энтропии всей системы в целом. Приращение энтропии в какой-либо части системы еще не говорит о росте потерь ее работы. Может случиться, что одновременно в другой части этой системы приращение энтропии уменьшится.

3. Все приведенные термодинамические зависимости справедливы для реальных адиабатных систем, включающих источники теплоты, рабочие тела и бесконечно емкую окружающую среду (с независимыми параметрами р₀,T₀).

0.2. Общие показатели термодинамической эффективности

термодинамических комплексов и систем

Под термодинамическими комплексами и системами мы понимаем термодинамические модели реальных энергетических комплексов и систем, представляющих собой, соответственно, сочетание взаимосвязанных агрегатов в одной энергетической установке или взаимосвязанное сочетание различных энергетических установок, тепловых и электрических сетей и преобразователей энергии, а в ряде случаев и энергетических потребителей. Все альтернативные варианты структур и режимов работы энергетических комплексов и систем должны обеспечить одинаковый энергетический эффект. При этом потребители во всех случаях должны получить нужное им количество энергии заданного качества. Для этой цели в энергосистемах предусматриваются резервные тепло- и электрогенерирующие мощности, а для покрытия пиковых нагрузок - пиковые энергоблоки и котельные установки. Эти дополнительные установки должны учитываться при составлении энергетических балансов системы. Учет вырабатываемой ими и расходуемой энергии, ее качества и потерь производится с помощью трех балансов: материального, энергетического (теплового) и эксергетического. Правильные результаты термодинамических расчетов и верные технические рекомендации можно получить только на основе совместного анализа всех трех балансов. В простейших случаях, когда в системе не совершается работа, а лишь используется теплота, можно ограничиться двумя балансами - материальным и тепловым. Однако, как правило, во всех энергосистемах вырабатываются и расходуются не только теплота, но и энергия направленного движения (электрическая, механическая, химическая), передаваемые в форме работы. По этой причине термодинамический анализ любых энергетических комплексов и систем должен производиться с помощью всех трех балансов с учетом показателей эффективности отдельных агрегатов и процессов.

М а т е р и а л ь н ы й б а л а н с. Составляется для всех теплоносителей и рабочих тел в виде равенства

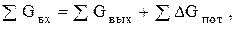(0.20)

где G_вх - масса веществ, поступивших в данную систему за определенный период времени; G_вых - масса веществ, ушедших из нее за тот же период времени; DG_пот - потери (утечки) вещества.

Коэффициент полезного использования массы данного вещества в используемой системе

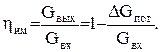(0.21)

Э н е р г е т и ч е с к и й (т е п л о в о й) б а л а н с. Составляется для всей системы или установки в целом и для отдельных агрегатов. При этом каждый вид энергии рассчитывается от одинакового (для всех видов) уровня отсчета и измеряется в джоулях. Основным уравнением теплового баланса является равенство

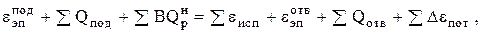(0.22)

где 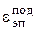и 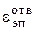- подведенная и отведенная электрическая энергия; Q_под и Q_отв - подведенная и отведенная теплота различного потенциала (с паром, водой и т.п.); 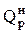- низшая теплотворная способность израсходованного топлива; В – расход топлива; 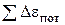- потери всех видов энергии, отведенные в окружающую среду в форме теплоты; - полезно использованная энергия.

В том случае, когда из системы отводятся вторичные энергоресурсы, величина SQ_отв определяется как располагаемая теплота этих ресурсов (через их теплоемкость и теплоту сгорания).

Коэффициент полезного использования энергии в данной системе определится как

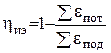, (0.23)

где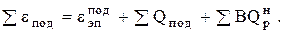

При составлении энергетического баланса теплоэнергетической системы или энергоустановки, где осуществляется производство электрической и/или тепловой энергии за счет сжигания органического топлива, целесообразно составлять тепловой баланс, определяющий степень использования теплоты его полного сгорания.

В этом случае, вместо 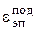и 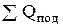в уравнение (0.22) вписывается полная теплота сгорания затраченных на выработку этих видов энергии топлив. При этом уравнение (0.22) составляют по отпущенной в сеть электрической (Э_отп) и тепловой (Q_отп) энергии, а также израсходованной на собственные нужды

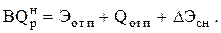
На основе такого баланса определяют коэффициент использования теплоты топлива

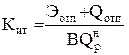. (0.24)

Если исследуемая установка или агрегат не вырабатывает электрической энергии и предназначается только для выработки теплоты (например, пара или горячей воды) данных параметров, то в этом случае K_ит превращается в тепловой КПД данного агрегата

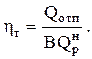(0.25)

В том случае, если энергоустановка предназначена для выработки только электрической энергии, ее совершенство оценивают по величине электрического КПД (нетто)

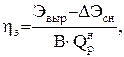(0.26)

где Э_выр - общая выработка электроэнергии; DЭ_сн - ее расход на собственные нужды установки.

Если же величина DЭ_сн не учитывается, то такой ее электрический КПД называется брутто. Все эти показатели широко применяются в теплотехнических расчетах, однако в ряде случаев являются недостаточными. Особенно это относится к показателю K_ит, при оценке совершенства энергоустановок, вырабатывающих комбинированным способом электрическую и тепловую энергии, поскольку в нем не учитываются качества (потенциал) последней. В этом случае требуется обязательное составление эксергетического баланса.

Э к с е р г е т и ч е с к и й б а л а н с. Составляется на основе первых двух балансов (массы и энергии) путем расчета потоков эксергии и ее потерь.

Очевидно, что эксергией электрической, механической и других видов энергии направленного движения будет являться сама величина этих энергий, которая определяется через максимально возможную их работу.

На этом основании в эксергетическом балансе эксергия рабочих тел и

теплоты непосредственно суммируется с электрической, механической и потенциальными энергиями (в том числе химической).

Соответственно этому уравнение эксергетического баланса имеет вид

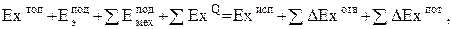(0.27)

где 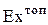- эксергия израсходованного топлива; 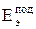- количество подведенной электрической энергии; 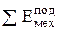- суммарное количество подведенной механической и другой энергии направленного движения; 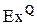- подведенная к системе эксергия теплоты различного потенциала; 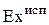- эксергия, полезно использованная в системе; 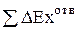- отведенная эксергия вторичных энергоресурсов; 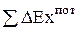- сумма эксергетических потерь.

Соответственно коэффициент использования располагаемой эксергии составит

. (0.28)

Наряду с этим определяют эксергетический коэффициент полезного действия системы или установки, под которым обычно понимают отношение полезно использованной к израсходованной в данной системе эксергии , то есть

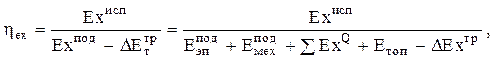(0.29)

где DEx^тр – «транзитная» часть эксергии, не используемая в данной системе.

0.3. Методы расчета максимальной работы
термодинамических систем и ее потерь

По своему определению эксергия системы представляет собой максимальную работу заданной системы, состоящей из источников энергии, рабочих тел и окружающей среды. Поэтому всегда максимальная работа системы определяется величиной ее эксергии.

Потери максимальной работы 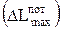всегда равны потерям эксергии и определяются через прирост энтропии системы

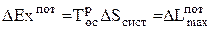. (0.30)

В зависимости от того, какой энергией обладают тела, входящие в состав термодинамической системы и как они воздействуют друг на друга, таков будет и вид их эксергии. В связи с этим различают следующие виды эксергии:

1. Эксергия неподвижного тела, находящегося в окружающей среде постоянного давления и температуры («эксергия объема»).

2. Эксергия тела в непрерывном потоке, обладающего энтальпией Н, скоростью движения W и потенциальной энергией полей П (эксергия потока).

3. Техническая эксергия, определяемая формулой (0.19).

4. Химическая эксергия, представляющая собой максимальную работу химических реакций при постоянных P = P₀ и T= T₀ (энергия Гиббса).

Рассмотрим теперь способы расчета каждой из этих видов эксергий.

Э к с е р г и я н е п о д в и ж н о г о т е л а. Определяется для G кг рабочего тела, у которого могут изменяться только внутренняя энергия U и энергия воздействия на него окружающей среды (P₀V). Располагаемая доля работы энергий такой системы составит

.

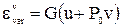Его эксергия, в соответствии с (0.17), составит

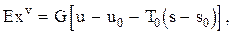(0.31)

где u₀, s₀ - параметры 1 кг рассматриваемого тела при его полном равновесии с окружающей средой.

В том случае, когда рабочее тело механически изолировано от окружающей среды и его объем изменяться не может

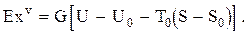(0.32)

Э к с е р г и я п о т о к а. Рассматривая 1 кг рабочего тела, находящегося в непрерывном движении внутри трубы, изменяющейся частью его энергии будет сумма энтальпии h, кинетической энергии 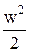и внешней потенциальной энергии полей, воздействующих на поток (гравитационного, электростатического и магнитного полей) п. Здесь, как и в случае неподвижного тела, оно может обмениваться теплотой с окружающей средой при T_o = T_oc. Это - обмен анергией.

Соответственно

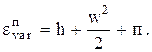(0.33)

Максимальная работа одного кг рабочего тела, которая может быть отведена от рассматриваемой системы согласно (0.33) будет равна эксергии потока

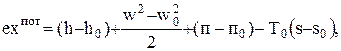(0.34)

где нижний индекс «о» показывает, что данный параметр соответствует полному равновесию системы при h₀, T₀. В расчетах теплоэнергетических установок обычно допускают w = w₀ и п = п₀. Тогда

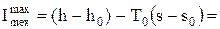ех. (0.35)

Величину 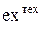называют удельной т е х н и ч е с к о й э к с е р г и- е й.

Х и м и ч е с к а я э к с е р г и я. Ее значение в расчетах теплоэнергетических установок определяется по разности потенциалов Гиббса

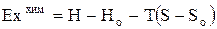, (0.36)

где H и H_o - суммарные абсолютные энтальпии реагирующих тел в начале и в конце реакции; S и S_o - суммарные энтропии этих же тел, отсчитанные от абсолютного нуля температур; T - температура начала и конца реакции.

Э к с е р г е т и ч е с к и е п о т е н ц и а л ы. Приведенные выше формулы расчета эксергии рабочих тел позволяют представить каждую из них через разность определенных термодинамических функций, представляющих собой термодинамические потенциалы эксергии. Так, если записать эксергию 1 кг неподвижного тела (0.31) в виде равенства

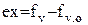, (0.37)

то его эксергетический потенциал будет равен

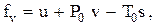(0.38)

а в случае u = const, получим

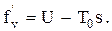(0.39)

Соответственно, эксергетический потенциал тела в потоке равен

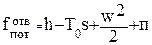(0.40)

а при определении максимальной технической работы

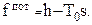(0.41)

Соответственно формуле (0.38) химический потенциал составит

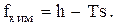(0.42)

В связи с тем, что эксергетические потенциалы при P_o = P_oc и T_o =T_oc, остаются в реальных процессах одинаковыми, приращение эксергии можно рассчитывать по формуле

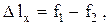(0.43)

где f₁ и f₂ - значения эксергетического потенциала в начальном и конечном состояниях тела.

Э к с е р г и я т о п л и в а. Эксергия расходуемого топлива Ex^топ представляет собой максимальную работу химической реакции системы топливо-воздух при стехиометрическом соотношении между ними. Она зависит от элементарного состава топлива и для упрощения расчетов используют приближенные формулы. В частности, эксергию твердых топлив можно рассчитать по формуле

(0.44)

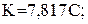
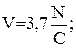
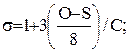
где 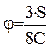; C,H,S,О,N - массовые доли соответственно углерода, водорода, кислорода, серы и азота.

Соответственно для нефтяных топлив

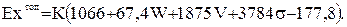(0.45)

Как показывает практика расчетов, эксергия топлив оказывается довольно близкой к их низшей рабочей теплотворной способности, отличаясь на постоянную величину в пределах 2-3 %. Поэтому с достаточной точностью в балансовых расчетах можно принимать . Несколько меньшую точность дают приближенные формулы для определения эксергии топлив по его высшей теплотворной способности . Так, для твердых топлив

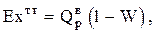(0.46)

где W- влагосодержание топлива.

Для жидких топлив

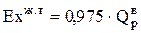, (0.47)

для газообразных топлив, в молекулах которых содержится более одного атома углерода, получим

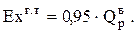(0.48)

Э к с е р г и я н е т т о. В ряде зарубежных стран для приближенной технико-экономической оценки проектируемых энергетических установок капитальные вложения на строительство заменяют израсходованной на их производство энергией или через соответствующую им эксергию. Так, затраченную эксергию на строительство любой электростанции определяют по формуле

, (0.49)

где M_i - масса i -й детали из соответствующего материала; W_д - минимальная работа разрушения породы и добычи сырья; DG - изменение энергии Гиббса для металлургического процесса; W_пр - минимальная работа деформации при прокате; W_обр - затраты работы на обработку, транспорт и другие операции всех элементов объекта. Все данные для таких расчетов берутся из специальных справочников.

Под эксергией нетто Ex^нт понимается разность между всей получаемой от данного объекта за весь период его работы эксергией Ex^max (электроэнергия + эксергия теплоты и пр.) и затраченной эксергией на его эксплуатацию SEx^экс и строительство SEx^стр. Под эксергией, затраченной на эксплуатацию, понимается не эксергия самих материалов и топлива, а та эксергия, которая затрачивается на их добычу, обработку и транспортирование

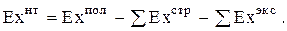(0.50)

Определив, таким образом, величину эксергии нетто для каждого альтернативного варианта проектируемой электростанции, можно предварительно оценить их экономическую эффективность.

Очевидно, что сооружать рассматриваемую установку можно только при условии Ex^нт > 0. В каком варианте получается большая величина Ex^нт, тот вариант более целесообразен.

Дата добавления: 2015-07-02