Методика расчета эксергетических КПД термодинамических циклов теплоэлектроцентралей

В зависимости от степени необратимости процессов различают:

- идеальные циклы, все процессы которых внешне и внутренне обратимы, а потери эксергии равны нулю;

- теоретические циклы, где соблюдается только внутренняя обрати- мость всех процессов, а теплообмен происходит при наличии разности температур, как между источниками теплоты и рабочими телами, так и между самими рабочими телами и теплоносителями;

- реальные циклы, в которых все процессы полностью необратимы. Здесь, как правило, все параметры рабочих тел и температурные напоры выбираются экономически наивыгоднейшими. Также должны обеспечиваться требования экологичности и надежности работы проектируемой установки.

Для оценки эффективности каждого из этих термодинамических циклов используются соответствующие эксергетические КПД. При этом эксергетический КПД любого идеального цикла ТЭЦ, где подводимая к 1 кг рабочего тела эксергия ex^Q теплоты горячего источника частично превращается в работу и частично отдается в форме теплоты 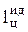, всегда будет

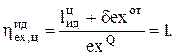(2.13)

Эксергетический КПД любого теоретического цикла ТЭЦ, равный в общем случае отношению суммы полезной работы l 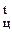и отданной потребителям эксергии теплоты 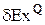к израсходованной эксергии теплоты топлива (Еx^Q) всегда будет меньше единицы из-за потерь в процессах теплообмена

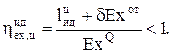(2.14)

Однако, чем меньше температурные напоры DT во всех процессах теплообмена теоретического цикла, тем ближе будет 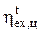к единице.

Совершенство реальных циклов ТЭЦ, отличающихся от идеальных и теоретических циклов не только полной необратимостью всех процессов, но и зависимостью каждой потери от параметров и свойств рабочих тел, оценивается двумя эксергетическими показателями. Первым из них является относительный эксергетический КПД реального цикла (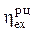), представляющий отношение cуммы реальной полезной работы цикла (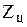) и отданной эксергии тепловым потребителям (dEx^R) к эксергии подведенной теплоты (Ex^Q)

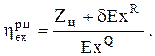(2.15)

Вторым показателем, учитывающим влияние цикла на процессы преобразования химической энергии топлива в теплоту газов, является абсолютный эксергетический КПД реального цикла, где сумма полезной работы цикла и эксергии отданной потребителям теплоты относится к эксергии сожженного топлива

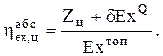(2.16)

Из сравнения формул (2.16) и (2.15) находим

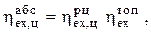(2.17)

где - энергетический КПД топки.

В свою очередь, эксергетический КПД реального цикла (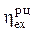) можно представить как произведение эксергетического КПД теоретического цикла 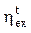на относительный внутренний КПД цикла 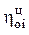, равный отношению действительной работы к теоретической

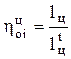, (2.18)

или с учетом (2.6)

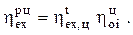(2.19)

С учетом этого формула (2.17) принимает вид

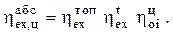(2.20)

Как показывают расчеты, между этими сомножителями существует взаимосвязь, которую необходимо раскрывать через параметры рабочего тела, температуры источников теплоты и другие характеристики цикла.

Покажем это на примере определения абсолютного эксергетического КПД простейшего цикла газотурбинной ТЭЦ, тепловая схема которой показана на рис. 2.5, а теоретический цикл - на рис. 2.6.

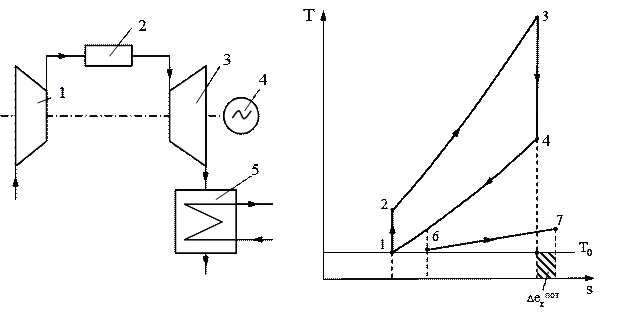
Рис. 2.5. Принципиальная схема Рис. 2.6. Термодинамический цикл

газотурбинной ТЭЦ: ГТУ – ТЭЦ

1–осевой компрессор; 2–камера сгорания; 3– газовая турбина;

4–электрогенератор; 5–котел-утилизатор

Напомним, что здесь рабочим телом являются продукты сгорания топлива, а поэтому приращение эксергии рабочего тела равно эксергии теплоты топлива DEx^рт = Ex^е и равно пл.1235. Для одного килограмма рабочего тела ее можно рассчитать по формуле

Dex^рт = h₃ - h₂ - T₀(s₃ - s₂), (2.21)

где h₃, s₃ - энтальпия и энтропия рабочего тела в точке 3 цикла; h₂, s₂ – то же в точке 2. Равная ей эксергия подведенной теплоты топлива равна

ex^Q = (h₃ - h₂) (1 - 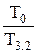), (2.22)

где Т_3.2 - среднетермодинамическая температура подвода теплоты в цикле.

Абсолютный эксергетический КПД реального цикла определится как

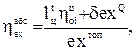(2.23)

где

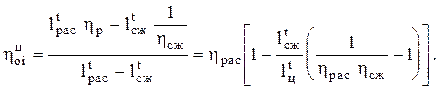(2.24)

Здесь величина отданной в сеть эксергии теплоты (dex^Q) может быть определена через эксергию отработавших газов (Dex^ог) и эксергетический КПД водогрейного котла-утилизатора 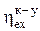. Отношение 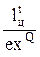представляет собой эксергетический КПД теоретического цикла

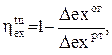(2.25)

а отношение­­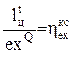 ­­­­- эксергетический КПД камеры сгорания. С учетом этих зависимостей формула (2.23) примет вид

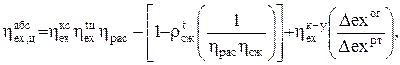(2.26)

где 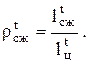(2.27)

Из полученных формул видно, что решающее влияние на величину абсолютного эксергетического КПД реального цикла газотурбинной ТЭЦ оказывают эксергетические КПД камеры сгорания (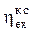) и теоретического цикла (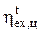), относительная работа сжатия теоретического цикла ( ­­­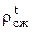) и эксергетический КПД котла-утилизатора, рассчитываемый как

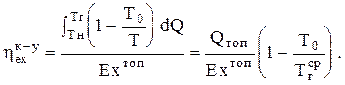(2.28)

Здесь абсолютная температура начала Т_н и окончания Т_г реакции горения топлива, а Т 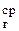- средняя температура тепловыделения, К.

Эксергетический КПД теоретического цикла, равный отношению теоретической работы цикла (l^t_рас - l^t_сж) к располагаемой эксергии, подводимой к рабочему телу теплоты (ex^рт), зависит главным образом от его внешней необратимости. Для безрегенеративных ГТУ открытого цикла, где рабочим телом являются сами продукты сгорания, решающее влияние на 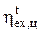оказывают температура выхлопных газов турбины и работа сжатия. Уменьшение работы сжатия, как правило, достигается многоступенчатым сжатием воздуха при его промежуточном охлаждении (рис. 2.7).

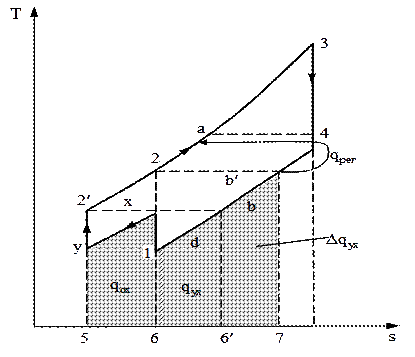
Рис. 2.7. Термодинамический цикл ГТУ
с двухступенчатым сжатием воздуха при его промежуточном охлаждении

Однако, как видно из этого рисунка, применение такого способа уменьшения 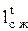при отсутствии регенерации снижает температуру воздуха (от точки 2 до точки 2^’ ) и тем самым уменьшает эксергетический КПД

всего цикла. По этой причине в низкотемпературных ГТУ применяют одноступенчатое сжатие. В таких циклах ТЭЦ большое влияние на их эффективность оказывают эксергетические потери в котле-утилизаторе, зависящие не только от температуры уходящих из него газов (точка 5, см. рис. 2.6), но и от величин верхних температур газов и нагреваемой воды (точки 4 и 7). Это подтверждается известной формулой потерь эксергии при передаче теплоты dQ от тела с температурой T₁ к телу с температурой T₂< T₁

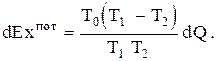(2.29)

Особо сильное снижение эксергетического КПД газовых циклов вызывает величина относительной работы сжатия их теоретического цикла

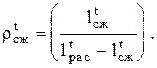(2.30)

Конструируя циклы ГТУ, всегда необходимо добиваться уменьшения этой величины.

Наименьшее влияние 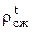оказывает на величину эксергетического КПД паротурбинных установок. В этом можно убедиться с помощью абсолютного эксергетического КПД реального цикла КЭС, равного отношению его работы Z к эксергии сожженного топлива Ex_т^топ, который можно рассчитать аналогично (2.26)

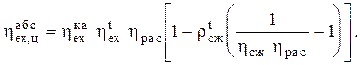(2.31)

Однако, учитывая, что r 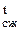в паровых циклах пренебрежительно мало (поскольку питательная вода несжимаема, а ее объем в сотни раз меньше объема пара) с достаточной точностью можно записать

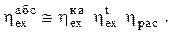(2.32)

При определении значения h_рас надо учесть влияние на его величину степени влажности пара в последних ступенях турбины. Взаимозависимость КПД котельного агрегата и термического КПД цикла можно выразить через конечную температуру регенеративного подогрева питательной воды.

Дата добавления: 2015-07-02