Ряды Фурье

Решение.

Решение.

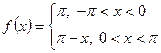
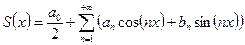
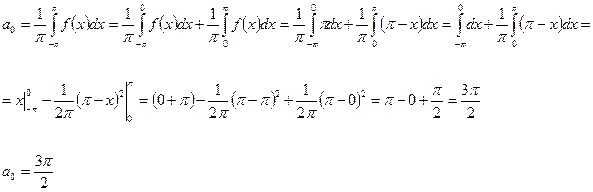
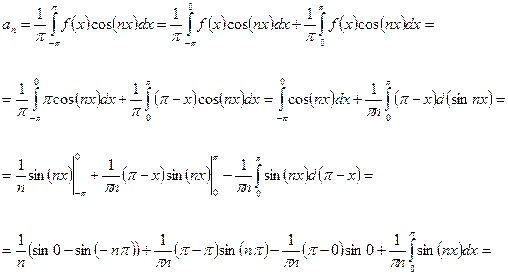
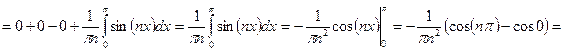
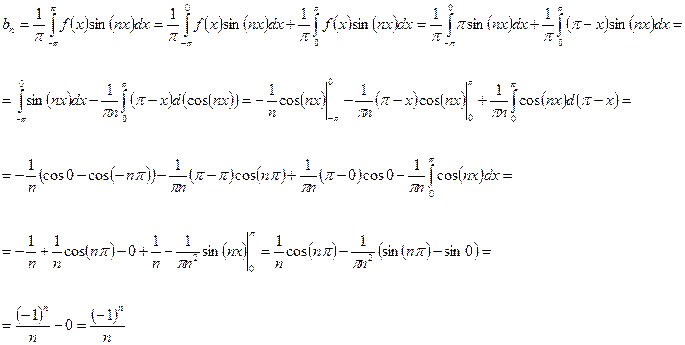
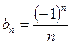
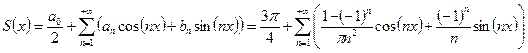
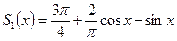
Исходная функция изображена зеленым цветом, а первое приближение 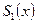- синим цветом. Десятое приближение 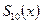изображено красным цветом.

Ответ.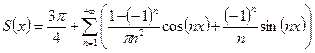

Задание 2.

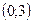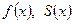Разложить в ряд Фурье по синусам на функцию . Начертить графики и её первого приближения.

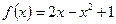
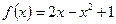
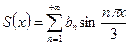
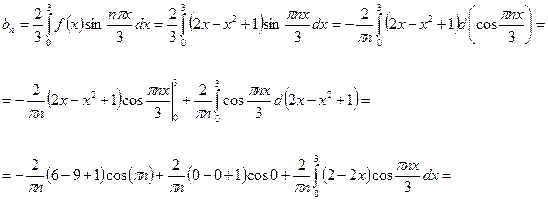
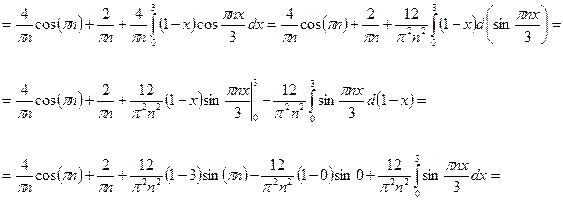
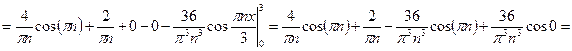
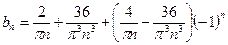
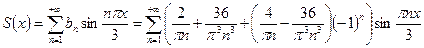
Исходная функция изображена зеленым цветом, а первое приближение 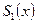- синим цветом. Восьмое приближение 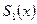изображено красным цветом.

Ответ.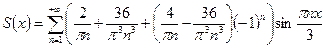

Существуют различные методы представления произвольной функции f(x) через более простые функции, свойства которых хорошо изучены. Так, ряд Тейлора представляет f(x) через сумму степенных функций. Если f(x) периодическая функция f(x) = f(x+T), то ее можно представить как сумму простейших тригонометрических функций типа A_n sin(nx + 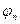). Такое разложение по кратным гармоникам наз. гармоническим анализом и оно очень удобно при рассмотрении радиотехнических задач. Электромагнитные волны это гармонические колебания, а всякий сложный радиосигнал это совокупность таких колебаний и его разложение на гармоники имеет реальный физический смысл.

Опр. Тригонометрическим наз. функциональный ряд из гармоник кратных частот

a₀/2 + 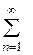a_ncos nx + b_nsin nx (19)

где коэффициенты ряда a_n, b_n действительные числа, n 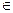N. Рассмотрим вопрос о сходимости такого ряда. Введем определения.

Опр. Всякий функциональный ряд 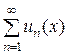наз. равномерно сходящимся на сегменте Х, если существует такой знакоположительный, сходящийся ряд , что | u_n| < v_{n ,} n 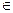N Ряд 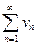наз. мажорирующим по отношению к исходному.

Равномерно сходящийся на сегменте Х ряд является в пределах сегмента абсолютно сходящимся и его можно почленно интегрировать.

Таким образом, из сходимости числового ряда 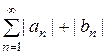следует равномерная сходимость ряда (19), т.к. |cos nx| < 1, |sin nx|< 1. Если ряд (19) равномерно сходится, то его сумма f(x) является периодической функцией с периодом T = 2 , т.к. все члены ряда имеют такой период.

Вопрос: существует ли простая связь между суммой ряда (19) S(x) и коэффициентами разложения a_n, b_n? Ответ: да, т.к. cos nx, sin nx образуют систему ортогональных функций.

Опр. Система функций u₁(x), u₂(x),..., u_n(x),... наз. ортогональной, если интеграл от произведения этих функций удовлетворяет условию

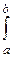u_i(x) u_j(x) dx = 0 при i 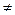j и = 1 при i = j (20)

Если функция f(x) разлагается в ряд по системе ортогональных функций { u_n }

f(x) = 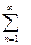c_n u_n, то ее коэффициенты равны c_n = 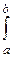f(x) u_n(x) dx. Эта формула получается после умножения ряда на u_n(x) и интегрирования с учетом (20).

Покажем, что тригонометрические функции { ½, sin x, cos x, sin 2x, cos 2x,... } образуют ортогональную систему на отрезке [- , ]со следующими свойствами

1. 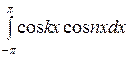= 0 при k 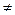n и = при k = n

2. 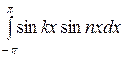= 0 при k 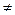n и = при k = n (21)

3. 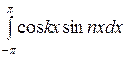= 0 4. 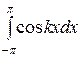= 0, = 0

Действительно, произведения тригонометрических функций сводятся к их сумме

sin a cos b = ½[sin(a+b) + sin(a-b)]; cos a cos b = ½[cos(a+b) + cos(a-b)]

sin a sin b = ½[cos(a-b) – cos(a+b)],

а интеграл по полному периоду от тригонометрической функции всегда равен 0. Исключение составляет интеграл

= ½ =

Простая связь между суммой ряда и его коэффициентами позволяет строить ряд под конкретную функцию.

Опр. Рядом Фурье для функции f(x) наз. тригонометрический ряд (18), который равномерно сходится и его сумма S(x) = f(x), т.е. построен под конкретную функцию.

Определим коэффициенты ряда Фурье. Для этого проинтегрируем его почленно и получим 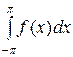= а₀ . Умножим все члены ряда (1) на сos kx и проинтегрируем с учетом соотношений (21). В результате получаем простые соотношения для произвольных коэффициентов ряда Фурье, которые зависят только от вида f(x):

а₀ = 1/ 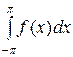; a_n = 1/ 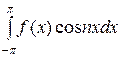; b_n = 1/ 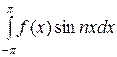(22)

Определим условия Дирихле: функция f(x) периода 2 на промежутке [- , ]

1) непрерывна или имеет конечное число точек разрыва 1 рода;

2) кусочно-монотонна, т.е. интервал разбивается на конечное число отрезков, где f(x) либо только возрастает, либо только убывает, либо постоянна.

Признак сходимости Дирихле. Если периодическая функция f(x) с периодом 2 удовлетворяет на любом отрезке из R условиям Дирихле, то ряд Фурье для функции f(x) сходится для всех х 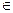R. При этом в каждой точке непрерывности функции х сумма ряда равна f(x), а в каждой точке разрыва а равна [f(a+0) + f(f-0)] /2, т.е. средне-арифметическому значению.

Если f(x) удовлетворяет условиям Дирихле, то она определяет на промежутке

[- , ] криволинейную трапецию конечной площади и является ограниченной функцией. Интегралы от произведения ограниченной функции на sin nx, cos nx т.е. a_n, b_n, быстро убывают с ростом n вне зависимости от вида f(x). Действительно, разобьем [- , ] на участки с шагом Dх = 2p/n и будем отдельно интегрировать в пределах каждого участка. Тогдапри больших n и малых Dх функция f(x)» const и

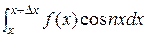» A 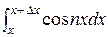= A/n sin nx 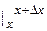= - A/n sin nx sin p = 0

Стремительное убывание a_n, b_n с ростом n обеспечивает сходимость мажорирующего ряда 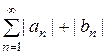и, следовательно, равномерную сходимость тригонометрического ряда(19)

Пр. Периодическая функция с периодом 2 определена как f(x) = x, 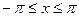. Разложить ее в ряд Фурье.

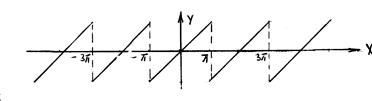
Решение. Функция удовлетворяет условиям Дирихле. Находим коэффициенты Фурье 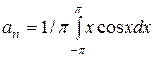= 0; 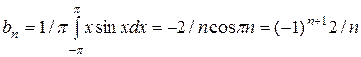Т.о. для х 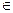R, кроме точек разрыва

f(x) = 2(sin x – sin 2x /2 + sin 3x /3 – sin 4x /4 +... + (-1)ⁿ⁺¹/n sin nx +...)

В точках разрыва x = 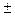(2n-1) сумма ряда [- (2n-1) + (2n-1) ]/2 = 0

Пр. Периодическая функция с периодом 2 определена как f(x) = 0 при 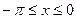и f(x) = 1 при 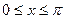. Разложить ее в ряд Фурье.

Решение. Функция удовлетворяет условиям Дирихле.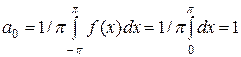

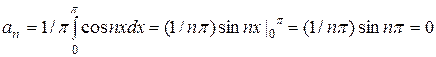
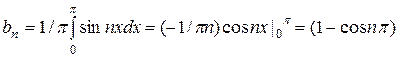= (1 – (-1)ⁿ) = {

Т.о. для всех х 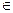R, кроме точек разрыва f(x) = ½ + 1/ 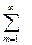[2/(2m -1)] sin(2m-1) x

В точках разрыва х = 0, 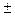n сумма ряда равна (0 + 1)/2 = ½.

Дата добавления: 2015-07-02