Следствия замкнутости тригонометрической системы

Условие равномерной сходимости.

Равномерная сходимость интегралов

При распространении изложенной теории интегралов, зависящих от параметра, на случай несобственных интегралов особую роль играет понятие равномерной сходимости интегралов, которое мы предварительно и выясним.

Пользуясь общим критерием равномерного стремления функции к пределу, можно применительно к рассматриваемому случаю сформулировать его так:

Следствие 1. Для любой кусочно-непрерывной на сегмен­те [—p,p] функции f(x) справедливо равенство Парсеваля.

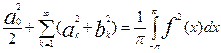(10.38)

(вытекает из теоремы 10.5).

Следствие 2. Тригонометрический ряд Фурье любой ку­сочно-непрерывной на сегменте [-p,p] функции f(х) сходится к этой функции на указанном сегменте в среднем (вытекает из теоремы 10.6 и замечания 2 к этой теореме).

Следствие 3. Тригонометрический ряд Фурье любой ку­сочно-непрерывной на сегменте [-p,p] функции f(х) можно почленно интегрировать на этом сегменте (вытекает из пре­дыдущего следствия и из теоремы 1.11 гл.1).

Следствие 4. Если две кусочно-непрерывные на сегмен­те

[-p,p] функции f(х) и g(х) имеют одинаковые тригоно­метрические ряды Фурье, то эти функции совпадают всюду на этом сегменте (вытекает из теоремы 10.8).

Следствие 5. Если тригонометрический ряд Фурье кусоч­но-непрерывной на сегменте [-p,p] функции f(х) сходится рав­номерно на некотором содержащемся в [-p,p] сегменте [a, b], то он сходится на сегменте [a, b] именно к функции f(x).

Доказательство. Пусть F(х) — та функция, к которой сходится равномерно на [а, b] тригонометрический ряд Фурье функции f(х). Докажем, что F(х)≡ f(х) всюду на сегменте [а, b]. Так как из равномерной сходимости на сегменте [а, b]вы­текает сходимость в среднем на этом сегменте (см. гл. 1, § 2, п. 3), то тригонометрический ряд Фурье функции f(x) сходится к функции F(х) на сегменте [а, b]в среднем. Это означает, что для произвольного ξ > 0 найдется номер n 1, начиная с которо­го n -я частичная сумма тригонометрического ряда Фурье S_n(x) удовлетворяет неравенству

(10.39)

С другой стороны, в силу следствия 2 последовательность S_n(х) сходится к f (х) в среднем на всем сегменте [-p,p], а ста­ло быть, и на сегменте [а, b], т. е. для фиксированного нами произвольного ξ> 0 найдется номер n₂ , начиная с которого

(10.40)

Из (10.39) и (10.40) и из неравенства треугольника

вытекает, что 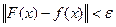. Из последнего неравенства и из произвольности ξ > 0 следует, что 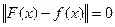, а отсюда на основании первой аксиомы для нормы заключаем, что F(x)-f(x) есть нулевой элемент пространства кусоч­но-непрерывных на [а, b]функций, т. е. функция, тождественно равная нулю на сегменте [a, b]. Следствие 5 доказано.

Замечание 1. Конечно, вследствие 5 сегмент [а, b]мо­жет совпадать со всем сегментом в данной точке т. е. из равномерной сходимости ряда Фурье функции f(х) на всем сегменте [—p,p] следует, что этот ряд сходится на указанном сегменте имен­но к функции f(x).

Замечание 2. Совершенно аналогичные следствия будут справед­ливы и для ряда Фурье по любой другой замкнутой ортонормированной си­стеме в пространстве кусочно-непрерывных на произвольном сегменте [а, b] функций со скалярным произведением (10.2) и нормой (10.8). Примерами таких систем могут служить указанные в § 1 ортонормированные системы, связанные с полиномами Лежандра и Чебышева, и система Хаара.

Дата добавления: 2015-07-02