Простейшие условия равномерной сходимости и почленного дифференцирования тригонометрического ряда Фурье

1. Вводные замечания. В математической физике и в ряде других разделов математики существенную роль играет вопрос об условиях, при выполнении которых тригонометрический ряд Фурье функции f/(х) сходится (к этой функции) в данной точке x сегмента [—p,p].

Еще в конце прошлого века было известно, что существу­ют непрерывные на сегменте [-p,p]функции, удовлетворяю­щие условию f(- p )=f( p ), тригонометрические ряды Фурье, которые расходятся в наперед заданной точке сегмента [-p,p] (или даже расходятся на бесконечном множестве точек сегмен­та [-p,p], всюду плотном на этом сегменте)[2]

Таким образом, одна непрерывность функции f(х) на сег­менте [-p,p] без дополнительных условий не обеспечивает не только равномерной сходимости тригонометрического ряда Фурье этой функции, но даже сходимости этого ряда в наперед заданной точке указанного сегмента.

В этом и в следующем параграфах мы выясним, какие тре­бования следует добавить к непрерывности функции f(х) (или ввести взамен непрерывности f(х)) для обеспечения сходимос­ти тригонометрического ряда Фурье этой функции в заданной точке, а также для обеспечения равномерной сходимости ука­занного ряда на всем сегменте [-p,p]или на какой-либо его части.

При изучении сходимости тригонометрического ряда Фурье возникает и другой вопрос: должен ли тригонометрический ряд Фурье любой кусочно-непрерывной (или даже строго непрерыв­ной) на сегменте [-p,p]функции f(х) сходиться хотя бы в одной точке этого сегмента?

Положительный ответ на этот вопрос был получен только в 1966 г.

Этот ответ является следствием фундаментальной теоремы, доказанной в 1966 г. Л. Карлесоном[3]) и решившей знамени­тую проблему Н. Н. Лузина[4]), поставленную еще в 1914 г.: тригонометрический ряд Фурье любой функции f(х), для ко­торой существует понимаемый в смысле Лебега интеграл 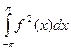, сходится к этой функции почти всюду на сегменте [-p,p] [5]).

Из теоремы Карлесона вытекает, что ряд Фурье не только любой кусочно-непрерывной, но и любой интегрируемой на сег­менте [-p,p] в собственном смысле Римана функции f(х) схо­дится к этой функции почти всюду на сегменте [-p,p](ибо для такой функции существует интеграл 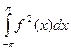в смысле Римана, а стало быть, и в смысле Лебега).

Заметим, что если функция f(х) интегрируема на сегменте [-p,p]не в смысле Римана, а только в смысле Лебега, то три­гонометрический ряд Фурье этой функции может не сходиться ни в одной точке сегмента [-p,p]. Первый пример интегрируе­мой на сегменте [-p,p]в смысле Лебега функции f(х) со всюду расходящимся тригонометрическим рядом Фурье был построен в 1923 г. советским математиком А. Н. Колмогоровым[6]).

2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье. Догово­римся о следующей терминологии.

Определение 1. Будем говорить, что функция f(х) имеет на сегменте [а, b] кусочно-непрерывную производ­ную, если производная f’(х) существует и непрерывна всюду на сегменте [а, b], за исключением, быть может, конечного числа точек, в каждой из которых функция f’(х) имеет ко­нечные правое и левое предельные значения [7]).

Определение 2. Будем говорить, что функция f(х) имеет на сегменте [а,b] кусочно-непрерывную производную порядкаn≥1, если функция f^(n-1)(x) имеет на этом сегменте кусочно-непрерывную производную в смысле определения 1.

Теорема 10.11. Если функция f(х) непрерывна на сегмен­те [-p,p], имеет на этом сегменте кусочно-непрерывную про­изводную и удовлетворяет условию f(- p ) = f( p ), то тригоно­метрический ряд Фурье функции f(х) сходится к этой функ­ции равномерно на сегменте [-p,p]. Более того, ряд, состав­ленный из модулей членов тригонометрического ряда Фурье функции f(х)_: сходится равномерно на сегменте [-p,p].

Доказательство. Достаточно доказать, что ряд, составленный из модулей членов тригонометрического ряда Фурье функции f(x),

(10.47)

сходится равномерно на сегменте [-p,p], ибо отсюда будет вы­текать как равномерная на сегменте [-p,p] сходимость самого тригонометрического ряда Фурье функции f(x), так и сходи­мость этого ряда (в силу следствия 5 из п. 3 § 3) именно к функ­ции f(x).

В силу признака Вейерштрасса (см. теорему 1.4 из гл. 1) для доказательства равномерной на сегменте [-p,p]сходимости ряда (10.41) достаточно доказать сходимость мажорирующего его числового ряда

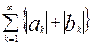(10.42)

Обозначим через α _k β_k тригонометрические коэффициенты Фурье функции f'(x), доопределив эту функцию произвольным образом в конечном числе точек, в которых не существует про­изводная функции f(х) [8]).

Производя интегрирование по частям и учитывая, что функ­ция f(х) непрерывна на всем сегменте [-p,p]и удовлетворяет соотношениям f(-p) = f(p), мы получим следующие соотно­шения, связывающие тригонометрические коэффициенты Фу­рье функции f '(х) и самой функции f(х) [9]):

,

.

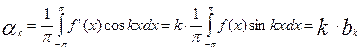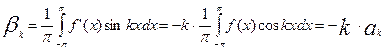Таким образом,

,

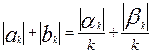и для доказательства ряда (10.42) достаточно доказать сходимость ряда

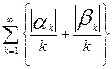. (10.43)

Сходимость ряда (10.43) вытекает из элементарных неравенств [10] )

,

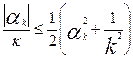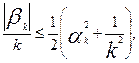(10.44)

и из сходимости рядов

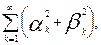
(10.45)

первый из которых сходится в силу равенства Парсеваля для кусочно-непрерывной функции f'(x), а второй — в силу интеграль­ного признака Коши-Маклорена (см. вып. 1, гл. 13, § 2). Теорема доказана.

Замечание. Если функцию f (х), удовлетворяющую усло­виям теоремы 10.11, периодически (с периодом 2 p) продолжить на всю бесконечную прямую, то теорема 10.11 будет утверждать сходимость тригонометрического ряда Фурье к так продолжен­ной функции, равномерную на всей бесконечной прямой.

3. Простейшие условия почленного дифференциро­вания тригонометрического ряда Фурье. Прежде всего до­кажем следующую лемму о порядке тригонометрических коэф­фициентов Фурье.

Лемма 1. Пусть функция f(х) и все ее производные до некоторого порядка т (т — целое неотрицательное число) не­прерывны на сегменте [-p,p] и удовлетворяют условиям

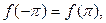
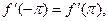
………… (10.46)

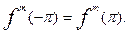
Пусть, кроме того, функция f(х) имеет на сегменте [-p,p] кусочно-непрерывную производную порядка (т + 1). Тогда схо­дится следующий ряд:

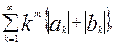(10.47)

в котором a_k и b_k суть тригонометрические коэффициенты Фурье функции f(x).

Доказательство. Обозначим через α_k и β_k тригономет­рические коэффициенты Фурье функции f^(k-1)(x), доопреде­лив эту функцию произвольным образом в конечном числе то­чек, в которых не существует производной порядка (m+1) функ­ции f(х). Интегрируя выражения для α_k и β_k(m+1) раз по частям и учитывая непрерывность на всем сегменте [-p,p] са­мой функции f(х) и всех ее производных до порядка m, а также учитывая соотношения (10.46), мы установим следующую связь между тригонометрическими коэффициентами Фурье функции f^(m+1)(x) и самой функции F(x)[11]):

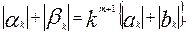
Таким образом,

,

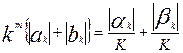и сходимость ряда (10.47) вытекает из элементарных неравенств (10.44) и из сходимости рядов (10.45), первый из которых сходит­ся в силу равенства Парсеваля для кусочно-непрерывной функ­ции f^(m+1)(x), а второй — в силу признака Коши-Маклорена. Лемма доказана.

Непосредственным следствием леммы 1 является следующая теорема.

Теорема 10.12. Пусть функция f(х) удовлетворяет тем же условиям, что и в лемме 1, причем т ≥ 1. Тогда тригоно­метрический ряд Фурье функции f(х) можно т раз почленно дифференцировать на сегменте [-p,p].

Доказательство. Пусть S — любое из чисел 1, 2,..., т. В результате s-кратного почленного дифференцирования три­гонометрического ряда Фурье функции f (х) получается ряд

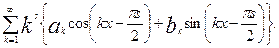(10.48)

Заметим, что для всех х из сегмента [-p,p] как исходный три­гонометрический ряд Фурье, так и ряд (10.48) (с любым s = 1, 2,..., m) мажорируется сходящимся числовым рядом (10.47). По признаку Вейерштрасса (см. теорему 1.4 из гл. 1) как исходный тригонометрический ряд Фурье, так и каждый из рядов (10.48) (при s = 1, 2,...,m) сходится равномерно на сегменте [-p,p], а это (в силу теоремы 1.9 из гл. 1) обеспечи­вает возможность m-кратного почленного дифференцирования исходного ряда Фурье. Теорема доказана.

[1] А стало быть (в силу теоремы 10.7) и полной.

[2] Первый пример такой функции был построен французским математи­ком Дю Буа Раймоном в 1876 г.

[3] Л. Карлесон – современный шведский математик. Полное доказательство теоремы Карлесона можно найти в сборнике переводных статей: “Математика”. 1967. Т. II, №4. С.113-132.

¹ Николай Николаевич Лузин – советский математик, основатель совре­менной московской математической школы по теории функций (1883-1950). Постановку проблемы Лузина, решенной Карлесоном, и других его проблем можно найти в книге Н. Н. Лузина «Интеграл и тригонометрический ряд». М.; Л.: Гостехиздат, 1951.

² Определение интеграла в смысле Лебега и сходимости почти всюду на данном сегменте см. в гл. 8 этой книги.

³ Построение примера А. Н. Колмогорова можно найти на с. 412-421 кни­ги Н. К. Бари «Тригонометрические ряды». М.: Физматгиз, 1961.

⁴ При этом При этом функция f'(х) может оказаться не определенной в конечном числе точек сегмента [а, b]. В этих точках мы доопределим ее произвольным образом (например, положим равной полусумме правого и левого предель­ных значений).

¹ Например можно положить функцию f'(x) в указанных точках равной полусумме правого и левого предельных значений.

[9] При интегрировании по частям следует разбить сегмент [—p,p]на ко­нечное число не имеющих общих внутренних точек частичных сегментов, на каждом из которых производная f '(х) непрерывна, и, беря формулу ин­тегрирования по частям для каждого из этих частичных сегментов, учесть, что при суммировании интегралов по всем частичным сегментам все под­становки обратятся в нуль (вследствие непрерывности f(x) на всем сегменте [— p, p ] и условий f(—p)=f(p)).

[10] Мы исходим из элементарного неравенства |а| • |b|≤(а² + б²)/2, выте­кающего из неотрицательности величины (|а| — |b|)².

[11] При интегрировании по частям сегмент [-p,p] следует разбить на ко­нечное число не имеющих общих внутренних точек частичных сегментов, на каждом из которых f^(m+1)(x) непрерывна, и учесть, что при суммирова­нии интегралов по всем частичным сегментам все подстановки дают нуль.

Дата добавления: 2015-07-02