Ряды Фурье

В естествознании и технике часто приходится иметь дело с периодическими процессами: колебательным и вращательным движением различных деталей машин и приборов, периодическим движением небесных тел и элементарных частиц, акустическими и электромагнитными колебаниями и т.п.

Математически все такие процессы описываются периодическими функциями. Простейшими периодическими функциями являются тригонометрические функции и 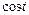с периодом 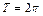. Основным вопросом настоящего раздела является вопрос о представлении произвольной периодической функции в виде суммы тригонометрических функций.

Ряды Фурье периода .Рядом Фурье периодической функции с периодом , определенной на отрезке 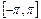, называется тригонометрический ряд

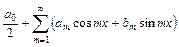, (9)

коэффициенты которого определяются формулами

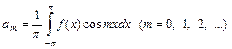, (10)

. (11)

Если ряд (9) сходится, то его сумма 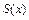есть периодическая функция с периодом , т.е. .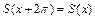

Теорема Дирихле. Пусть функция на отрезке 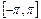имеет конечное число экстремумов и является непрерывной за исключением конечного числа точек разрыва 1-го рода. Тогда ряд Фурье этой функции сходится в любой точке отрезка 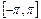и сумма 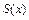этого ряда:

1) 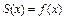во всех точках непрерывности функции , лежащих внутри отрезка ;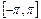

2) 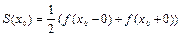, где 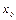- точка разрыва первого рода функции ;

3) на концах промежутка, т.е. при .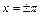

Ряды Фурье периода2l. Если периодическая функция с периодом 2l задана на отрезке 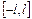, то при выполнении на этом отрезке условий теоремы Дирихле указанная функция может быть представлена в виде суммы ряда Фурье

,

где

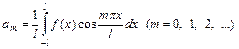, (12)

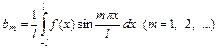. (13)

Ряд Фурье четной функции содержит только свободный член и косинусы 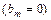; ряд Фурье нечетной функции содержит только члены с синусами .

Если функция задана на отрезке , то для разложения в ряд Фурье достаточно доопределить ее на отрезке 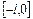произвольным способом, а затем разложить в ряд Фурье, считая ее заданной на отрезке 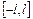. Наиболее целесообразно функцию доопределить так, чтобы ее значения в точках отрезка 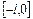находились из условия 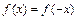или 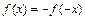. В первом случае функция на отрезке 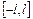будет четной, а во втором – нечетной.

Пример.

Разложить в ряд Фурье периодическую функцию с периодом , заданную на интервале .

Решение.

Определяем коэффициенты ряда Фурье по формулам (10) и (11).

.

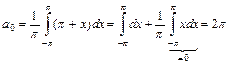Далее, находим коэффициенты :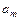

.

Первый интеграл равен нулю, т.к.

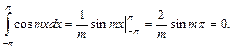
Второй интеграл равен нулю, как интеграл от нечетной функции, взятый по интервалу, симметричному относительно начала координат.

Найдем теперь коэффициенты :

.

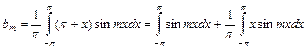Первый интеграл равен нулю, как интеграл от нечетной функции. Подынтегральная функция второго интеграла – четная как произведение двух нечетных функций. Таким образом,

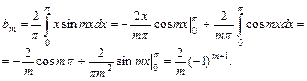
Следовательно, разложение функции в ряд Фурье имеет вид

.

Пример.

Разложить в ряд Фурье периодическую функцию , заданную на полупериоде .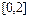

Решение.

Функция может быть разложена в ряд Фурье бесчисленным количеством способов. Рассмотрим два наиболее важных разложения.

1) Доопределим функцию на отрезке 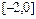четным образом (рис. 1).

Тогда все коэффициенты .

.

.

Итак,

.

2) Доопределим функцию на отрезке 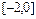нечетным образом (рис. 2).

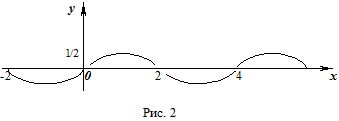
Тогда все коэффициенты .

.

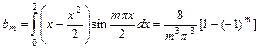Итак,

.

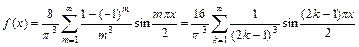Дата добавления: 2015-07-02