
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операции над рядами Фурье. Полнота и замкнутость
731. Почленное интегрирование ряда Фурье. Предположим функцию f (х), как обычно, абсолютно интегрируемой в промежутке 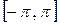 . Пусть ее ряд Фурье будет
. Пусть ее ряд Фурье будет
 ~
~ 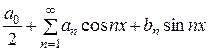 . (1)
. (1)
Введем в рассмотрение для  функцию
функцию
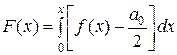 , (2)
, (2)
очевидно, непрерывную и с ограниченным изменением [486, 7°, 568, 4°]; к тому же она имеет период  , ибо
, ибо
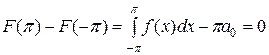 . (3)
. (3)
В таком случае, по теореме п ° 686, эта функция во всем промежутке разлагается в ряд Фурье:
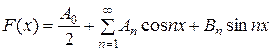 . (4)
. (4)
(который к тому же, согласно 699, равномерно сходится к ней).
Между коэффициентами рядов (1) и (4) существует простая связь. Действительно, если воспользоваться обобщенной формулой интегрирования по частям, установленной в п ° 580, (9), то будем иметь (для  ):
):
 ,
,
то есть
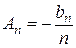 .
.
Аналогично, на этот раз с учетом равенства (3), получим
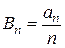 .
.
Для нахождения же А 0 положим в (4) х = 0:
 . (5)
. (5)
Подставив в разложение (4) найденные значения коэффициентов, можем переписать его в виде
 .
.
Отсюда, если учесть равенство (2), имеем
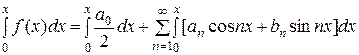 . (6)
. (6)
Очевидно, и для любого промежутка [  ], где
], где 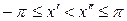 , имеет место подобное же соотношение:
, имеет место подобное же соотношение:
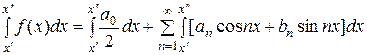 .
.
Таким образом, интеграл от функции f (х) получается почленным интегрированием соответствующего ей ряда Фурье. Тот факт, что почленное интегрирование ряда Фурье оказывается всегда допустимым, тем более замечателен, что мы установили его, даже не делая предположения о сходимости самого ряда (1) к функции f (х)!
Ясно, что в качестве основного промежутка вместо 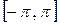 может быть выбран любой другой промежуток длины
может быть выбран любой другой промежуток длины  . Точно так же все сказанное относится и к рядам, содержащим одни лишь косинусы или одни лишь синусы [689] и рассматриваемым в промежутке [0,
. Точно так же все сказанное относится и к рядам, содержащим одни лишь косинусы или одни лишь синусы [689] и рассматриваемым в промежутке [0, 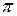 ].
].
Интегрированием известных тригонометрических разложений могут быть получены другие разложения. Член  в (6), если угодно иметь тригонометрическое же разложение, следует перенести в другую часть равенства. Некоторого внимания требует к себе свободный член
в (6), если угодно иметь тригонометрическое же разложение, следует перенести в другую часть равенства. Некоторого внимания требует к себе свободный член 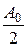 : получить его в конечном виде удается либо непосредственным суммированием ряда (5), либо же интегрированием по формуле
: получить его в конечном виде удается либо непосредственным суммированием ряда (5), либо же интегрированием по формуле

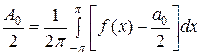 .
.
Поясним это примером. Если проинтегрировать разложение
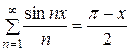
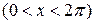
[см. 690, (2)] от 0 до х, то получим:
 .
.
Отсюда
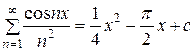
 ,
,
причем с определяется либо как сумма ряда
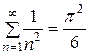 ,
,
либо как интеграл:
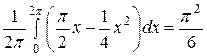 .
.
Таким образом, мы приходим к разложению, которое независимо было получено в 690, (9). Аналогично разложение в (7) (а) получается из разложения в (7) (б) и т.д.
Замечание. Подчеркнем, что проведенным рассуждением попутно установлен такой факт: какова бы ни была абсолютно интегрируемая в промежутке 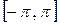 функция f (х), ряд
функция f (х), ряд
 ,
,
где bn – коэффициенты при синусах в ее ряде Фурье, необходимо сходится [ср. 692, 2°]. Ниже, в 758, мы воспользуемся этим замечанием.
732. Почленное дифференцирование ряда Фурье. Пусть в промежутке 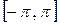 задана непрерывная функция f (х), удовлетворяющая условию
задана непрерывная функция f (х), удовлетворяющая условию  и имеющая (исключая разве лишь отдельные точки в конечном числе) производную
и имеющая (исключая разве лишь отдельные точки в конечном числе) производную  ; пусть, далее, эта производная сама оказывается абсолютно интегрируемой в названном промежутке. Тогда
; пусть, далее, эта производная сама оказывается абсолютно интегрируемой в названном промежутке. Тогда

[310, 481] и, как мы только что видели, ряд Фурье (1) функции f (х) получается из ряда Фурье функции 
 ~
~ 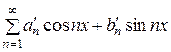 . (7)
. (7)
почленным интегрированием, так как при наложенных на f (х) условиях свободного члена в последнем разложении не будет:
 .
.
В таком случае, очевидно, и обратно – ряд (7) для производной  может быть получен из ряда (1), отвечающего данной функции f (х), почленным дифференцированием.
может быть получен из ряда (1), отвечающего данной функции f (х), почленным дифференцированием.
Мы обращаем особое внимание читателя на ту роль, которую здесь играет предположение о периодичности функции f (х). При нарушении этого условия свободный член  ряда Фурье для
ряда Фурье для  был бы отличен от нуля, и уже по одному этому упомянутый ряд не мог бы быть получен из ряда (1) почленным дифференцированием! Например, в случае разложения (а – не целое)
был бы отличен от нуля, и уже по одному этому упомянутый ряд не мог бы быть получен из ряда (1) почленным дифференцированием! Например, в случае разложения (а – не целое)
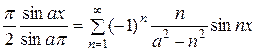
[664, (7) (б)] почленное дифференцирование приводит к ряду
 ,
,
который заведомо никаким рядом Фурье быть не может, ибо его коэффициенты даже не стремятся к нулю [682].
Замечание. До сих пор мы говорили о возможности получения ряда Фурье (7) для производной  путем почленного дифференцирования ряда Фурье исходной функции f (х). При этом вовсе не было речи о сходимости ряда (7) к функции
путем почленного дифференцирования ряда Фурье исходной функции f (х). При этом вовсе не было речи о сходимости ряда (7) к функции  ; эту сходимость надлежит устанавливать особо, пользуясь теми или другими достаточными признаками [684, 686].
; эту сходимость надлежит устанавливать особо, пользуясь теми или другими достаточными признаками [684, 686].
Нужно отметить, что, ввиду появления при дифференцировании 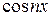 и
и 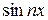 натуральных множителей п, порядок малости коэффициентов понижается и ухудшаются шансы на сходимость. Между тем, при решении с помощью рядов Фурье задач математической физики часто приходится дифференцировать эти ряды, и даже неоднократно. Для обеспечения сходимости получаемых рядов иногда оказывается полезным предварительное выделение плохо сходящихся частей по методу А. Н. Крылова [710]. При этом сумма выделенной части, известная в конечном виде, дифференцируется непосредственно, а для остающегося ряда стараются добиться столь высокого порядка малости коэффициентов, чтобы и после дифференцирования получить все же равномерно сходящийся ряд.
натуральных множителей п, порядок малости коэффициентов понижается и ухудшаются шансы на сходимость. Между тем, при решении с помощью рядов Фурье задач математической физики часто приходится дифференцировать эти ряды, и даже неоднократно. Для обеспечения сходимости получаемых рядов иногда оказывается полезным предварительное выделение плохо сходящихся частей по методу А. Н. Крылова [710]. При этом сумма выделенной части, известная в конечном виде, дифференцируется непосредственно, а для остающегося ряда стараются добиться столь высокого порядка малости коэффициентов, чтобы и после дифференцирования получить все же равномерно сходящийся ряд.
733. Полнота тригонометрической системы. Если непрерывная в промежутке 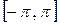 функция f (х) имеет коэффициенты Фурье, все равные нулю, то и сама функция сводится тождественно к нулю. Действительно, в этом случае, как ясно из равенства (6), при всех х будет
функция f (х) имеет коэффициенты Фурье, все равные нулю, то и сама функция сводится тождественно к нулю. Действительно, в этом случае, как ясно из равенства (6), при всех х будет
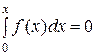 ,
,
откуда, дифференцируя по х, именно ввиду непрерывности подинтегральной функции [806, 12°] и получим тождественно

Иными словами, кроме функции, тождественно равной нулю, не существует непрерывной функции, которая в промежутке 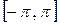 * была бы ортогональна [679] ко всем функциям тригонометрической системы
* была бы ортогональна [679] ко всем функциям тригонометрической системы
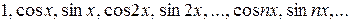 (9)
(9)
Этот именно факт и выражают, говоря, что тригонометрическая система полна — в классе непрерывных функций.
Если две непрерывные функции f 1(х) и f 2(х) имеют одни и те же коэффициенты Фурье, то они необходимо тождественны, ибо их разность 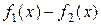 будет иметь коэффициенты Фурье, сплошь равные нулю. Таким образом, непрерывная функция однозначно определяется своими коэффициентами Фурье. Это лишь другая формулировка свойства полноты тригонометрической системы.
будет иметь коэффициенты Фурье, сплошь равные нулю. Таким образом, непрерывная функция однозначно определяется своими коэффициентами Фурье. Это лишь другая формулировка свойства полноты тригонометрической системы.
Если обратиться к рассмотрению и разрывных функций, то положение вещей может оказаться другим. Функция, которая, скажем, лишь в конечном числе точек отлична от нуля, уже не равна нулю «тождественно, но в то же время, очевидно, будет ортогональна к любой из функций (9), как, впрочем, и ко всякой интегрируемой (в собственном или несобственном смысле) функции. Можно представить себе функции, отличные от нуля даже в бесконечном множестве точек и все же обладающие последним свойством. Такова, например, функция f (х) [ср. 70, (8), 300, (1)], равная 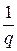 , если х есть несократимая дробь вида
, если х есть несократимая дробь вида  , а в прочих точках промежутка
, а в прочих точках промежутка 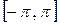 равная 0.
равная 0.
Однако функция, которая в рассматриваемом промежутке ортогональна ко всякой вообще интегрируемой функции, не отличается «существенно» от нуля; мы будем называть такую функцию эквивалентной нулю.
Теперь можно доказать, что абсолютно интегрируемая в промежутке 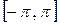 функция f (х), коэффициенты Фурье которой все равны нулю, необходимо эквивалентна нулю.
функция f (х), коэффициенты Фурье которой все равны нулю, необходимо эквивалентна нулю.
Действительно, если g (х) — произвольная функция, интегрируемая в собственном смысле, то, в силу 579, 1о,
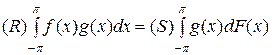 ,
,
где  . При сделанных предположениях
. При сделанных предположениях 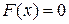 [см. (8)], так что f (х) ортогональна к g (х).
[см. (8)], так что f (х) ортогональна к g (х).
Отсюда легко перейти к случаю, когда g (х) интегрируема в несобственном смысле. Пусть, например, точка я будет ее единственной особой точкой. Тогда, полагая 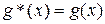 в
в 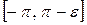
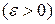 и
и 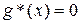 в
в 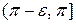 , по доказанному будем иметь
, по доказанному будем иметь
 .
.
Остается лишь перейти к пределу при 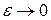 .
.
Расширяя несколько понятие «полноты», можно утверждать теперь, что тригонометрическая система (9) полна в классе абсолютно интегрируемых функций. Смысл этого таков: кроме функций, эквивалентных нулю, не существует абсолютно интегрируемой функции, которая в промежутке 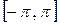 была бы ортогональна ко всем функциям (9).
была бы ортогональна ко всем функциям (9).
Наконец, если две абсолютно интегрируемые функции имеют одни и те же коэффициенты Фурье, то их разность эквивалентна нулю. Если не считать такие функции «существенно» различными, то в некотором смысле можно сказать и здесь, что абсолютно интегрируемая функция однозначно определяется своими коэффициентами Фурье.
Замечание. Все сказанное сохраняет свою силу и порознь для систем

или
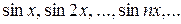
но лишь в промежутке [0, 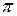 ].
].
734. Равномерная аппроксимация функций. Теоремы Вейер-штрасса. Если какую-либо функцию f (x) в промежутке [ а, b ] «аппроксимируют»* с помощью другой, g (x), то качество этой аппроксимации можно, в зависимости от обстоятельств, оценивать по-разному. Но, естественно, в основу во всех случаях кладется рассмотрение разности
 .
.
Если мы одинаково заинтересованы в малом отклонении одной из функций от другой во всех отдельно взятых точках, то за меру приближения принимают их максимальное отклонение в промежутке, т. е. Число
 .
.
В этом случае говорят о равномерной аппроксимации функции f (x) с помощью функции g (x).
Мы приведем две фундаментальные теоремы Вейерштрасса, относящиеся к равномерной аппроксимации непрерывных функций, во-первых, с помощью тригонометрических многочленов и, во-вторых, с помощью обыкновенных (алгебраических) многочленов.
Теорема 1. Если функция f(x) непрерывна в промежутке [ 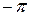 ,
, 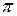 ] и удовлетворяет условию
] и удовлетворяет условию
 ,
,
то, каково бы ни было число  >0, найдется такой тригонометрический многочлен
>0, найдется такой тригонометрический многочлен
 ,
,
что равномерно для всех значений х в упомянутом промежутке будет
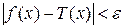 . (10)
. (10)
Построим прежде всего такую кусочно-линейную функцию 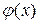 , чтобы повсюду в [
, чтобы повсюду в [ 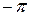 ,
, 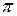 ]выполнялось неравенство
]выполнялось неравенство
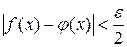 . (11)
. (11)
Для этого разобьем промежуток [ 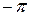 ,
, 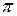 ] точками
] точками
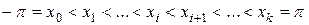
на столь малые части, чтобы в каждой из них колебание функции f было  . Функцию
. Функцию 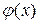 определим в промежутке [
определим в промежутке [ 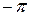 ,
, 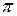 ], полагая ее в каждом отдельном промежутке [ хi, хi +1] равной линейной функции
], полагая ее в каждом отдельном промежутке [ хi, хi +1] равной линейной функции
 ,
,
которая на концах промежутка совпадает с f (x). По сути дела речь идет о вписывании ломаной линии в кривую, выражаемую уравнением y = f (x). Если через mi и Мi обозначить наименьшее и наибольшее значения функции f в i -м промежутке, то по условию  , и так как в этом промежутке значения обеих функций f и
, и так как в этом промежутке значения обеих функций f и 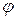 содержатся между mi и Мi, то выполнение неравенства (11) во всем промежутке [
содержатся между mi и Мi, то выполнение неравенства (11) во всем промежутке [ 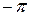 ,
, 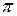 ] удостоверено.
] удостоверено.
Функция 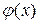 подобно f (x) непрерывна в промежутке [
подобно f (x) непрерывна в промежутке [ 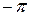 ,
, 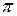 ] и удовлетворяет условию
] и удовлетворяет условию
 ;
;
но, сверх того, она, как кусочно-монотонная функция, имеет в этом промежутке ограниченное изменение [668, 1°]. При этих условиях, согласно признаку Дирихле-Жордана [699], 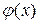 разлагается в равномерно сходящийся ряд Фурье:
разлагается в равномерно сходящийся ряд Фурье:
 .
.
Следовательно, если в качестве многочлена Т (х) взять n -ю частичную сумму этого ряда при достаточно большом п, то он будет отличаться от 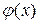 меньше, чем на
меньше, чем на 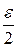 :
:
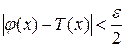 . (12)
. (12)
сразу для всех рассматриваемых значений х.
Из (11) и (12) вытекает (10).
Возьмем теперь последовательность  убывающих до нуля положительных чисел и для каждого числа
убывающих до нуля положительных чисел и для каждого числа  построим многочлен Т = Tk (x), о котором была речь в доказанной теореме; тогда получится последовательность
построим многочлен Т = Tk (x), о котором была речь в доказанной теореме; тогда получится последовательность 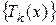 тригонометрических многочленов, которая сходится к функции f (x) равномерно в промежутке [
тригонометрических многочленов, которая сходится к функции f (x) равномерно в промежутке [ 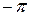 ,
, 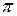 ]. Переходя обычным образом [427] от последовательности к бесконечному ряду, получим другую формулировку теоремы, очевидно, равносильную прежней: при указанных в теореме 1 условиях функция f (x) разлагается в равномерно сходящийся ряд, членами которого являются тригонометрические многочлены.
]. Переходя обычным образом [427] от последовательности к бесконечному ряду, получим другую формулировку теоремы, очевидно, равносильную прежней: при указанных в теореме 1 условиях функция f (x) разлагается в равномерно сходящийся ряд, членами которого являются тригонометрические многочлены.
Из теоремы 1 уже легко выводится
Теорема 2. Если функция f (x) непрерывна в промежутке [ а, b ], то, каково бы ни было число 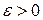 , найдется такой целый алгебраический многочлен
, найдется такой целый алгебраический многочлен
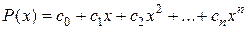 ,
,
что равномерно для всех значений х в [ а, b ] будет
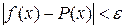 . (13)
. (13)
Простой подстановкой
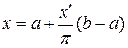
можно свести дело к рассмотрению промежутка [0, 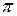 ], ибо многочлен, целый относительно
], ибо многочлен, целый относительно  , очевидно, будет целым и относительно х. Чтобы не усложнять обозначений, будем считать, что первоначально данный промежуток и есть [0,
, очевидно, будет целым и относительно х. Чтобы не усложнять обозначений, будем считать, что первоначально данный промежуток и есть [0, 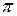 ].
].
Распространим теперь функцию f (х) на весь промежуток [ 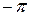 ,
, 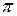 ], полагая
], полагая
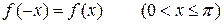 .
.
Функция сохранит непрерывность и, очевидно, будет удовлетворять условию  . В таком случае по теореме 1 найдется такой тригонометрический многочлен Т (х), что для всех значений х между
. В таком случае по теореме 1 найдется такой тригонометрический многочлен Т (х), что для всех значений х между 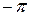 и
и 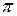 будет
будет
 . (14)
. (14)
Если заменить каждую из тригонометрических функций, входящих в состав Т, ее разложением по степеням х [404], то и функция Т представится в виде суммы повсюду сходящегося степенного ряда:
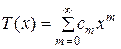 .
.
В промежутке [ 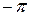 ,
, 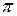 ] этот ряд сходится равномерно; поэтому, если отождествить многочлен Р (х) с n -й частичной суммой этого ряда, при достаточно большом п, то для всех х в промежутке [
] этот ряд сходится равномерно; поэтому, если отождествить многочлен Р (х) с n -й частичной суммой этого ряда, при достаточно большом п, то для всех х в промежутке [ 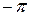 ,
, 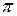 ] будет
] будет
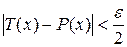 . (15)
. (15)
Остается сопоставить (14) и (15).
Как и выше, доказанной теореме можно дать другую формулировку: функция f (x), непрерывная в промежутке [ а, b ], разлагается в этом промежутке в равномерно сходящийся ряд, членами которого являются целые алгебраические многочлены.
735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье. При аппроксимации функции f (х) в промежутке [ а, b ] с помощью другой функции g (x) можно стать и на другую точку зрения, предпочитая вместо равномерной близости этих функций требовать, чтобы функции были близки лишь «в среднем». В этом случае за меру близости их можно взять их среднее отклонение
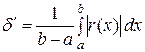
или, чего мы и будем держаться в последующем, среднее квадратичное отклонение
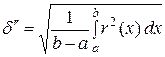 .
.
Вместо этого выражения, впрочем, удобнее рассматривать более простую величину:
 .
.
Обратимся вновь к рассмотрению произвольной ортогональной в промежутке [ а, b ] системы функций 
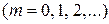 , интегрируемых с их квадратами [679]. Пусть f (x) — заданная в том же промежутке функция, также интегрируемая с квадратом, ил — фиксированное натуральное число. Поставим себе такую задачу: из всех линейных комбинаций первых
, интегрируемых с их квадратами [679]. Пусть f (x) — заданная в том же промежутке функция, также интегрируемая с квадратом, ил — фиксированное натуральное число. Поставим себе такую задачу: из всех линейных комбинаций первых 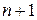 функций
функций 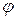
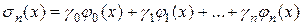 (16)
(16)
при произвольном наборе коэффициентов  ,
, 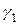 , …,
, …, 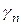 найти ту, которая осуществляет наилучшее — в смысле среднего квадратического отклонения — приближение к функции f (x). Иными словами, требуется добиться наименьшего значения для величины
найти ту, которая осуществляет наилучшее — в смысле среднего квадратического отклонения — приближение к функции f (x). Иными словами, требуется добиться наименьшего значения для величины
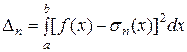 .
.
Подставив сюда вместо 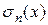 ее развернутое выражение, получим:
ее развернутое выражение, получим:
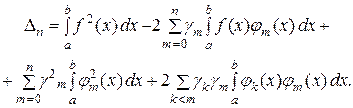
Последняя сумма исчезает ввиду ортогональности нашей системы. Вводя постоянные
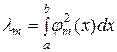
и (обобщенные) коэффициенты Фурье функции f (x)
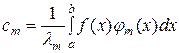 ,
,
можно переписать выражение для  в виде
в виде
 .
.
Чтобы под знаком суммы получить полные квадраты, нужно ввести туда еще члены  . Добавив их с плюсами и с минусами, окончательно получим:
. Добавив их с плюсами и с минусами, окончательно получим:
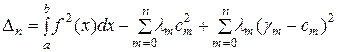 .
.
Теперь ясно, что  достигает своего наименьшего значения тогда, когда обращается в нуль последняя сумма, а это будет при
достигает своего наименьшего значения тогда, когда обращается в нуль последняя сумма, а это будет при
 ,
, 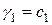 , …,
, …, 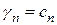 .
.
Таким образом, из всех многочленов вида (16) именно отрезок (обобщенного) ряда Фурье
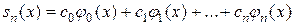
доставляет величине  наименьшее возможное для нее значение
наименьшее возможное для нее значение
 . (17)
. (17)
Снова наше внимание приковывается к коэффициентам Фурье как, и некотором смысле, «лучшим» из всех возможных! Важно отметить при этом, что коэффициенты, оказавшиеся «лучшими» при фиксированном п, сохраняют свою роль и при больших значениях п, к ним лишь присоединяются еще новые коэффициенты!
Равенство (17) называют тождеством Бесселя. Из него получаются неравенства

и (если перейти к пределу при 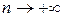 )
)
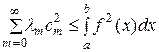 . (18)
. (18)
Это — неравенство Бесссля. Любопытно, что ряд в (18) оказывается всегда сходящимся, лишь бы функция f (x) была интегрируема с квадратом.
При возрастании п величина  убывает, поскольку в ее выражении (17) добавляются новые отрицательные слагаемые. Чем больше п, тем ближе сумма sn (x) «в среднем» подходит к рассматриваемой функции f (x). Естественно возникает вопрос: можно ли за счет увеличения п добиться сколь угодно малого среднего квадратического отклонения, т. е. стремится ли
убывает, поскольку в ее выражении (17) добавляются новые отрицательные слагаемые. Чем больше п, тем ближе сумма sn (x) «в среднем» подходит к рассматриваемой функции f (x). Естественно возникает вопрос: можно ли за счет увеличения п добиться сколь угодно малого среднего квадратического отклонения, т. е. стремится ли  к 0 при
к 0 при 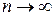 ?
?
Если это выполняется, то говорят, что сумма sn (x) сходится к функции f (x) «в среднем» (что — подчеркнем это — вовсе не предполагает «точечной» сходимости sn (x) к f (x) в обычном смысле слова). Из тождества Бесселя ясно, что тогда (и только тогда), имеет место равенство [ср. (18)]:
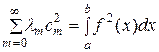 .
.
Следуя В. А. Стеклову, мы будем называть его уравнением замкнутости. Обычно, впрочем, его называют формулой Парсеваля (М. A. Parseval), по имени ученого, который еще в начале XIX века рассматривал подобную формулу для тригонометрической системы (без какого-либо обоснования).
Если уравнение замкнутости выполняется для каждой функции f (x), интегрируемой с квадратом, то саму систему  называют замкнутой.
называют замкнутой.
Применим теперь все сказанное в частности к тригонометрической системе (9). Вместо сумм вида (16) придется рассматривать тригонометрические многочлены

и исследовать осуществляемое ими приближение «в среднем», которое характеризуется величиной
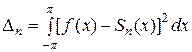 .
.
Оказывается, что при фиксированном п наименьшее значение этой величине доставляет соответствующий отрезок ряда Фурье
 .
.
Само же это наименьшее значение дается равенством
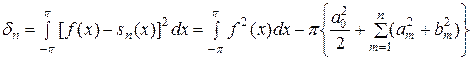 . (19)
. (19)
(«тождество Бесселя»). Из него вытекает, как и в общем случае, сходимость ряда, составленного из квадратов коэффициентов Фурье:
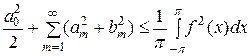
(«неравенство Бесселя»).
Для рассматриваемой конкретной системы (9) мы в состоянии полностью решить поставленный в общем случае вопрос, что и будет выполнено в следующем п °.
736. Замкнутость тригонометрической системы. Теорема Ляпунова. Имеет место следующая замечательная теорема, строгое доказательство которой (для случая ограниченной функции) впервые было дано А. М. Ляпуновым.
Теорема. Какова бы ни была интегрируемая с квадратом функция f (x), всегда
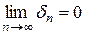 ,
,
и выполняется «уравнение замкнутости»
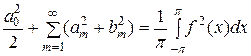 . (20)
. (20)
Доказательство мы разобьем на несколько этапов.
1°. Если функция f (x) непрерывна в промежутке  и удовлетворяет условию
и удовлетворяет условию  , то по первой теореме Вейер-штрасса существует такой тригонометрический многочлен Т (х) (порядок которого мы здесь обозначим через N), что
, то по первой теореме Вейер-штрасса существует такой тригонометрический многочлен Т (х) (порядок которого мы здесь обозначим через N), что
 ,
,
где  — произвольное наперед заданное положительное число. Тогда
— произвольное наперед заданное положительное число. Тогда
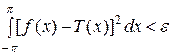 .
.
По экстремальному же свойству отрезка ряда Фурье [736], поскольку Т (х) при желании можно рассматривать как тригонометрический многочлен любого порядка  , и подавно, при
, и подавно, при 
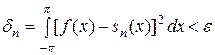 ,
,
так что  при
при 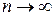 .
.
2°. Для того чтобы распространить это заключение и на другие случаи, установим одно вспомогательное неравенство.
Если интегрируемая с квадратом функция f (x) представляется в виде суммы  двух подобных же функций, то, обозначая штрихами относящиеся к ним величины, будем иметь
двух подобных же функций, то, обозначая штрихами относящиеся к ним величины, будем иметь
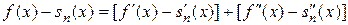 ,
,
откуда
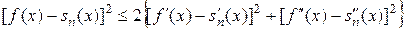 *
*
и, далее,
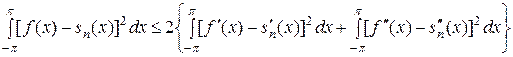
или, короче:
 .
.
Заметим, наконец, что из тождества Бесселя [см. (19)], примененного к функции f, следует
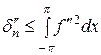 .
.
Таким образом, окончательно
 . (21)
. (21)
Это и есть нужное нам неравенство.
3°. Пусть теперь функция f (х) будет интегрируема в собственном смысле (а значит ограничена) в промежутке  . Изменяя в случае надобности значение функции на одном из концов промежутка, можно считать, что
. Изменяя в случае надобности значение функции на одном из концов промежутка, можно считать, что  . Построим вспомогательную функцию
. Построим вспомогательную функцию 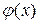 , как мы делали это при доказательстве первой теоремы Вейерштрасса [734], причем дробление промежутка на этот раз выберем так, чтобы было
, как мы делали это при доказательстве первой теоремы Вейерштрасса [734], причем дробление промежутка на этот раз выберем так, чтобы было
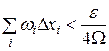 ,
,
где  — наперед взятое по произволу положительное число,
— наперед взятое по произволу положительное число, 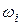 — колебание функции f в i -м частичном промежутке, а
— колебание функции f в i -м частичном промежутке, а 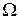 — полное колебание функции f во всем промежутке от
— полное колебание функции f во всем промежутке от 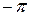 до
до 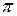 [297].
[297].
Мы положим
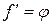 ,
,  .
.
В силу 1°, 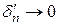 при
при 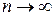 , так что, начиная с некоторого места,
, так что, начиная с некоторого места,
 .
.
С другой стороны, так как в i -й частичном промежутке
 ,
,
то
 .
.
Теперь, ввиду (21), уже ясно, что для достаточно больших п будет
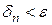 ,
,
и т. д.
4°. Пусть, наконец, функция f (x) будет интегрируема в несобственном смысле, но обязательно с квадратом. Для простоты предположим, что при этом единственной особой точкой для f (и для f 2) будет 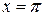 . Тогда по заданному
. Тогда по заданному 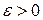 можно найти такое
можно найти такое  , что будет
, что будет
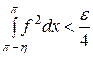 .
.
Положим в этом случае

и, наоборот,

Очевидно,
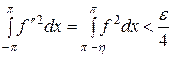 .
.
С другой стороны, к функции f, интегрируемой в собственном смысле, приложим только что доказанный результат. С помощью (21) заключаем, что и здесь  . Этим завершается доказательство теоремы Ляпунова.
. Этим завершается доказательство теоремы Ляпунова.
Пользуясь установленной в предыдущем п ° терминологией, можно сказать, что тригонометрическая система является замкнутой.
737. Обобщенное уравнение замкнутости. Пусть даны две функции f (x) и 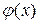 , интегрируемые в промежутке
, интегрируемые в промежутке  с квадратами. Как известно [483, 6], тогда функции
с квадратами. Как известно [483, 6], тогда функции 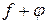 и
и  также будут интегрируемы с квадратами. Если обозначить, соответственно, через аm, bm и
также будут интегрируемы с квадратами. Если обозначить, соответственно, через аm, bm и  ,
, 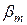 коэффициенты Фурье функций f и
коэффициенты Фурье функций f и 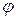 то для функций
то для функций  очевидно, коэффициентами Фурье будут
очевидно, коэффициентами Фурье будут 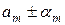 ,
, 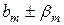 .
.
Применив уравнение замкнутости порознь к функциям  и
и  , получим:
, получим:

и
 .
.
Если почленно вычесть эти два равенства одно из другого, то, принимая во внимание тождество
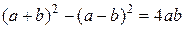 ,
,
придем к обобщенному уравнению замкнутости
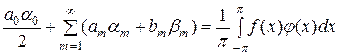 . (22)
. (22)
Уравнение (20) получается отсюда при  . Эту общую формулу также называют формулой Парсеваля.
. Эту общую формулу также называют формулой Парсеваля.
* Глава XIX была посвящена, главным образом, разложению функций в сходящиеся ряды Фурье; в ней эти ряды излучились как вычислительный аппарат. В настоящей же главе мы становимся на более общую точку зрения и изложим ряд важных вопросов, представляющих преимущественно теоретический интерес.
* Или в каком-нибудь другом промежутке длины 2 
* То есть приближенно воспроизводят.
* Мы пользуемся здесь элементарным неравенством 
|
Дата добавления: 2015-07-02; Просмотров: 2284; Нарушение авторских прав?; Мы поможем в написании вашей работы!