
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Учебный материал. Корреляционный анализ
|
|
|
|
Корреляционный анализ
Практическое занятие 3
Корреляционный анализ – это совокупность методов математической статистики, предназначенных для установления факта наличия или отсутствия взаимосвязей, взаимозависимости между двумя или несколькими количественными показателями (признаками).
В рамках корреляционного анализа используются следующие приемы:
- оценка парной корреляции – позволяет исследовать связь между двумя показателями;
- множественная корреляция – для оценки зависимости одного показателя от группы показателей;
- каноническая корреляция – для анализа связи между группами показателей;
- частная корреляция - позволяет исследовать связь между двумя показателями, элиминируя влияние других показателей;
- ранговая корреляция – для анализа связей между качественными показателями.
Для исследования связи между двумя показателями, имеющими нормальное распределение, используется коэффициент парной корреляции:
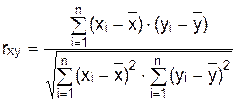 (-1 £ rxy £ +1),
(-1 £ rxy £ +1),
где:
X, Y – случайные величины, распределенные по нормальному закону;
xi – i-тое наблюдение показателя X,
yi – i-тое наблюдение показателя Y,
 – выборочное среднее показателя X (центр группировки),
– выборочное среднее показателя X (центр группировки),
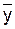 – выборочное среднее показателя Y (центр группировки).
– выборочное среднее показателя Y (центр группировки).
Положительный знак коэффициента парной корреляции означает, что с увеличением одной переменной увеличивается и другая, отрицательный – что с увеличением одной другая уменьшается.
Абсолютная величина коэффициента означает силу связи (условно принимаем: 0 – 0,3 – слабая связь, 0,3 – 0,7 – связь средней силы, 0,7 – 1 – сильная связь). Связь между показателями может быть полной, то есть функциональной, тогда коэффициент равен 1 или -1, а может вовсе отсутствовать, тогда коэффициент равен 0. Если зависимость неполная, поскольку она искажена влиянием других, посторонних факторов, то коэффициент будет принимать промежуточные значения (между –1, 0, 1) в зависимости от тесноты связи. Например, производительность труда зависит от стажа работы, но реально существуют и другие факторы, изменяющие эту зависимость (здоровье и т.п.).
С помощью коэффициента корреляции можно получить ответы на следующие вопросы:
- есть ли связь между показателями X и Y?
- насколько тесна связь между показателями X и Y?
Сильная корреляция означает закономерность: чем более отличается от своего среднего значение одной переменной, тем дальше от своего среднего значение другой. При этом нужно помнить, что коэффициент корреляции применим только в отношении случайных величин, имеющих нормальное распределение.
Корреляционный анализ непосредственно не выявляет причинные связи, он только устанавливает численное значение силы этих связей. Более того: корреляция не есть причина. В результате применения корреляционного анализа исследователь устанавливает только один факт - есть или нет связь между двумя переменными, изменяется одна переменная вместе с другой или нет. Необходимо отдавать себе отчет в том, что наличие связи ничего не говорит о ее причине, о том, чем данная связь может быть обусловлена. Причина взаимосвязи переменных может, как заключаться в одной из этих переменных, так и лежать вне рассматриваемых явлений.
Пример.
Требуется оценить тесноту взаимосвязи ряда показателей, характеризующих студентов вуза N:
Y – Успеваемость по предмету (бал.)
X1 – Посещаемость лекций (%)
X2 – Материальное положение (бал.)
X3 – Отношение к преподавателю (бал.)
| Испытуемые (студенты) | Успеваемость | Посещаемость | Материальное положение | Отношение к преподавателю |
| 5,0 | ||||
| 4,5 | ||||
| 4,6 | ||||
| 5,0 | ||||
| 3,2 | ||||
| 4,5 | ||||
| 2,4 | ||||
| 2,2 | ||||
| 3,5 | ||||
| 4,7 | ||||
| 4,3 | ||||
| 3,1 | ||||
| 3,6 | ||||
| 2,4 | ||||
| 4,5 | ||||
| 4,9 | ||||
| 5,0 | ||||
| 3,0 | ||||
| 4,1 | ||||
| 4,9 | ||||
| 4,0 | ||||
| 3,0 | ||||
| 4,8 | ||||
| 2,0 | ||||
| 4,9 | ||||
| 4,2 | ||||
| 3,6 | ||||
| 4,8 | ||||
| 4,0 | ||||
| 3,4 |
Содержание корреляционного анализа
| № | Y | X1 | X1 - 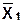
| Y1 - 
| (X1 - 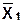 )2 )2
| (Y1 -  )2 )2
| (X1 - 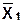 )´
(Y1 - )´
(Y1 -  ) )
| ||||||
| 5,0 | 20,2 | 1,1 | 409,4 | 1,1 | 21,5 | ||||||||
| 4,5 | 4,2 | 0,6 | 17,9 | 0,3 | 2,4 | ||||||||
| 4,6 | 10,2 | 0,7 | 104,7 | 0,4 | 6,8 | ||||||||
| … | |||||||||||||
| 3,4 | 9,2 | -0,5 | 85,3 | 0,3 | -5,0 | ||||||||
| Среднее | 3,9 | 79,8 | |||||||||||
| Сумма | 7109,4 | 25,1 | 350,4 | ||||||||||

|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 215; Нарушение авторских прав?; Мы поможем в написании вашей работы!