Суматори

Суматор - пристрій, що виконує операцію додавання двох чисел.

Суматори багаторозрядних двійкових чисел зазвичай будуються на основі однорозрядного комбінаційного суматора. При цьому кожний із суматорів, що оперує з багаторозрядними доданками, в залежності від способу обробки чисел, може бути віднесений до послідовного чи рівнобіжного типу. Додавання чисел у послідовних суматорах здійснюється порозрядно, послідовно в часі. У суматорах рівнобіжної дії додавання всіх розрядів багаторозрядних чисел відбувається одночасно.

По числу входів розрізняють два типи однорозрядних комбінаційних суматорів: напівсуматор що, має два входи а і b (мал. 2.23 а); повний суматор, що має три входи а, b, р
(мал. 2.23 6).

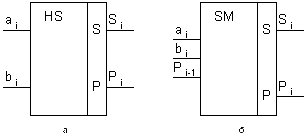
Рис. 2.23. Умовне графічне позначення однорозрядного напівсуматора (а) і повного сумматора (б)

Складемо таблицю істинності напівсуматора (табл. 2.12) і по ній запишемо функцію обчислення суми S_i а також переносу одиниці переповнення рі в старший розряд:

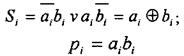(2.16)

Таблиця 2.12

аш	bi	S	Рi

З метою економії числа логічних елементів структурна формула для 8і складена по нулях, а для переносу Р_i по одиницях

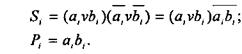(2.17)

Перетворимо вираз(2.17) для реалізації напівсуматора на елементах І-НІ:

(2.18)

Схеми напівсуматорів побудовані відповідно до виразів (2.16) і (2.18), показані на мал.2.24 а,б.

Вибір схеми для реалізації визначається наявної в напівсуматора розпорядженні розробника елементною базою з урахуванням вимог по швидкодії, енергоспоживанню і технологічності.

Робота повного суматора описується табл. 2.13. Цей пристрій призначений для додавання трьох однорозрядних двійкових чисел а, b, Р_{i -1} де Р_{i -1} - сигнал переносу з попереднього молодшого розряду. Подібно до напівсуматора повний суматор має два виходи 5_i, (сума) і Р_i (перенос).

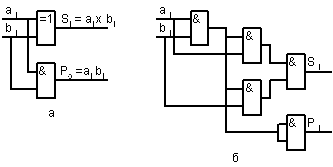
Рис. 2.24. Логічна структура напівсуматора, реалізована на основі логічного елемента що включає АБО і коньюктора (а) і в базисі елементів І-НІ (б)

У табл. 2.13 зв'язані всі можливі варіанти значень і- го розряду, що виникають при додаванні двох двійкових чисел А і В, і результат додавання (функції 5_i i P _i).

Таблиця 2.13

Входи	Виходи
a i	bi	Рі-1	Si	Pi

Виходячи з таблиці істинності суматора табл. 2.13, можна написати наступні булеві рівняння для сигналів суми і переносу:

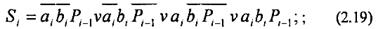
(2.20)

Перетворивши вираз (2.19) і (2.20), отримаемо

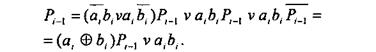(2.21)

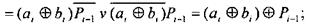
реалізація повного суматора.

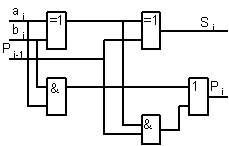
Рис. 225. Комбінаційний однорозрадний повний суматор.

Зі схеми мал. 2.25 видно, що повний суматор складається з двох напівсуматорів (мал. 2.26). Операція додавання трьох однорозрадних чисел у цій схемі розбивається на дві операції додавання двох однорозрадних чисел. Спочатку в першому напівсуматорі додаються числа a_i і b_i,а потім у другому напівсуматорівиконується додавання суми цих чисел S з числом Р_i-l. З табл.2.13 видно, що перенос у старший розряд виникає або коли a_i=b_i= 1, або коли одиниці рівні а_i або b_i і є сигнал переносу Р_i-l з попереднього розряду. У схемі мал.2.26 у першому випадку сигнал переносу в старший розряд формується першим напівсуматором (Р'=1), у другому – другим напівсуматором (Р'' = 1). Тому сигнал на виході повного суматора знімається з АБО схеми, на входи якої подаються сигнали Р' і Р ".

Рис. 2.26. Комбінаційний однорозрядний повний суматор, реалізований на двох напівсуматорах

Додавання багаторозрядних чисел можна реалізувати послідовно або паралельно. При послідовному введенні використовується один загальний для всіх розрядів повний суматор з додатковим ланцюгом затримки (мал. 2.27,а). Обидва складаються послідовно, починаючи з молодшого розряду, і результат переносу від додавання на попередньому такті подаються на входи суматора. Ланцюг затримки забезпечує збереження імпульсу переносу Р1 на час одного такту, тобто до приходу пари доданків наступного розряду, з якими він буде просумований Затримку забезпечує D-тригер (тригер затримки) (мал. 2.27,б). Для збереження і введення доданків a_i i b_i а також для запам'ятовування і збереження результату підсумовування використовуються регістри зсуву (мал.2.27,в).

Достоїнством послідовного сумратора є простота схеми, що вимагає мінімальної кількості устаткування, що не залежить від розрядності чисел, що сумуються. Недоліком є низька швидкодія, тому що для додавання кодів п- розрядних чисел потрібно (п+1) такт роботи пристрою. Додатковий такт необхідний для реалізації переносу від підсумовування старших розрядів. Однак тривалість операції підсумовування пропорційна розрядності операндів, тому послідовний суматор може використовуватися у відносно повільнодіючих цифрових пристроях.

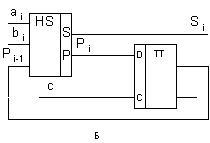
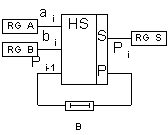
Рис. 2.27. Послідовний багаторозрядний суматор з ланцюгом затримки (а), D - тригером (б), з регістрами зсуву чисел А, В і їхньої суми (в)

На мал. 2.28 показана схема, що пояснює принцип дії п-розрядного рівнобіжного суматора з послідовним переносом. Число суматорів тут дорівнює числу розрядів. Вихід переносу р кожного суматора з'єднаний із входом переносу наступного, більш старшого розряду. На вході переносу суматора першого розряду встановлені потенціали, оскільки сигнал переносу сюди не надходить.

Після того, як сформується результат додавання на виходах однорозрядних суматорів, він зазвичай запам'ятовується в паралельному регістрі. Тривалість формування результату визначається часом встановлення вихідних сигналів (як суми, так і переносу з однорозрядних суматорів після встановлення сигналів на його входах. При цьому, якщо на входи a_і і b_i усіх розрядів сигнали надходять у момент початку такту, то на вхід P_i сигнал переносу надійде з деякою затримкою, обумовленою тривалістю перехідних процесів t₃ в суматорі попереднього розряду. У суматорі з порозрядним послідовним переносом, яким є суматор, зображений на мал. 2.28, сигнал поширюється послідовно від розряду до розряду в міру утворення суми в кожному окремому розряді. Для найгіршого випадку час поширення переносу t_nep = nt_зд при великій розрядності п чисел А і В може виявитися неприпустимо великим.

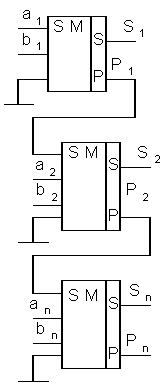
Рис. 2.28. Рівнобіжний n-розрядний сумаатор з послідовним переносом

Час переносу можна зменшити, ввівши паралельний перенос, для чого застосовують спеціальні вузли - блоки прискореного (наскрізного) переносу. Принцип прискореного переносу полягає в тім, що для кожного двійкового розряду додатково знаходяться два сигнали: утворення переносу G і поширення переносу Н. Ці функції визначаються в такий спосіб:

G_i =a_i b_i

H_i=a_i vb_i .

У випадку G _i=1, тобто. a_i =b_i =1, у даному і-му розряді формується сигнал переносу P_i у наступний вищий розряд незалежно від формування функцій суми в попередніх розрядах. Якщо хоча б один з доданків a_i або b_i дорівнює одиниці (тобто H _i = 1), то перенос у наступний розряд відбудеться при наявності сигналу переносу з попереднього розряду. Якщо функції поширення переносу в двох сусідніх розрядах рівні одиниці, тобто. H_i = H_{i +1} = 1, і при цьому існує сигнал переносу Р_{i +1} з попереднього розряду, то перенос виконується безпосередньо в розряд номер і+2.

Процес формування прискореного переносу описується наступним рівнянням:

P_i =G_i v Н_i G_i-1 vН_i Н_i-1 G_i-2 v...vH _i H _i-1 ...H₂H _i P₀

У серіях інтегральних мікросхем є одне-, двох- і чотирьохразрядні суматори, які можна об'єднати для одержання суматорів з будь-якою розрядністю. У серію ДО155, наприклад, входять суматори: ДО155НІХ1 - однорозрядний (мал.2.29,а), ДО155ІХ2 -дворозрядний (мал,2.29,б), ДО155ІМЗ - чотирирозрядний (мал. 2.29,в). У серіях ДО176 і ДО561 мається чотирирозрядний суматор ЇМ1 (мал. 2.29,г). МікросхемаДО155НІХ1 являє собою повний однорозрядний суматор і призначений для побудови багаторозрядних схем додавання і вирахування з паралельною обробкою вхідної інформації і послідовною передачею сигналів переносу. Завдяки ускладненій вхідній і вихідній логіці суматор володіє великими функціональними можливостями. Багаторозрядні суматори і пристрої віднімання на його основі організуються без додаткових логічних елементів і можуть працювати в позитивній і негативній логіці. Суматор К155ІМ1 зручний також для застосування в схемах з послідовним підсумовуванням.

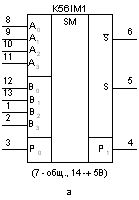
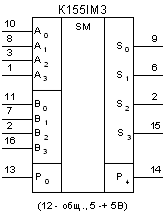
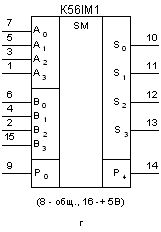
Мал.2.29. Однорозрядний (а),дворозрядний(б) і чотирирозрядний

(у,г) суматори

Принцип роботи дворозрядногосуматора К155ІМ2 і чотирирозрядного K155ІM3 однаковий. Дія їх базується на рівнобіжному підсумовуванні даних у різних розрядах при послідовному переносі з розряду в розряд. Вхід переносу P₀ є тільки в молодшого розряду, а вихід - тільки в старшого. Особливо зручна для застосування в апаратурі мікросхема К155ІМЗ: наявність чотирьох розрядів і можливість нарощування дозволяють використовувати її для виконання різних арифметичних операцій. При послідовному з'єднанні мікросхем з метою нарощування розрядності вихід переносу безпосередньо з'єднують із входом переносу мікросхем, що належать більш високим розрядам.

Мікросхему К155ІМ3 можна використовувати також як два незалежних суматора: дворозрядний і однорозрядний (мал. 2.30). суматорі доданки подають на входи А_о, В_о (з урахуванням Р_о) і А₁ В₁. Входи А₂, В₂ заземлюють. Результатом підсумовування служать сигнали на виходах S_o S₁ а сигналом переносу сигнал на виході S₂. Склади однорозрядного суматора подаються на входи A₃ і В₃. Сума знімається з виходу S₃, а перенос – з виходу Р₄. Мікросхема K561IM1 є чотирирозрядним суматором зі схемою прискореного переносу.

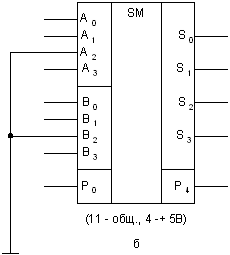
Рис. 2.30. Мікросхема К155ІМЗ у ролі дворозрядного й однорозрядного суматора

Для віднімання двох чисел можуть буті зібрані напіввіднімаючі і віднімаючі пристрої (напівсубтрактори і субтрактори). Напіввіднімаючий пристрій за принципом дії має два входи: для зменшуваного і для від’ємника, і тому може бути використаний тільки у вищому розряді багаторозрядного віднімального пристрою. В усіх інших розрядах повинні бути повні віднімаючі пристрої, що мають третій вхід для прийому сигналу позики.

У виді самостійних виробів віднімаючі пристрої виробляються. У випадку потреби віднімаючі пристрої (субтрактори) можна зпроектувати подубно тому, як це робилося для суматора. Таблиця істиності субтрактора (табл.2.14) описує роботу напівсуматора, а його логічна схема показана на мал.2.31.

Таблиця 2.14

a	b	Різниця	Позика

У пристоях цифрової техніки операція віднімання зазвичай замінюється додаванням зменшуваного з від’ємником, представленним у додатковому коді.

Чотирирозрядний суматор К155ІМЗ можна застосовувати в якості віднімаючого пристою. Операція віднімання виконується шляхом додавання зменшуваного з від’ємником, взятим у додатковому коді. На мал.2.32,а показано як це робиться.

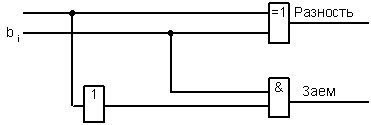
Мал.2.31. Логічна структура напівсубтрактора

Віднімаємо В = В₃ В₂В₁ В₀ за допомогою чотирьох інверторів перетвориться в зворотний код, і до нього по входу Р_о додається одиниця. Результат додавання числа А = А ₃А₂А ₁А_{) з числом В у додатковому коді формується на виходах S₃,S₂,S₁ S_o. Тут S₀ = A₀ + В_о + 1 (за рахунок Р_о = 1); S_l =A_l + В₁; S₂ = А₂ + В₂;S₃ = А₃ + В₃. Біт вищого розряду відкидається, тому вихід переносу Р₄ залишається вільним.

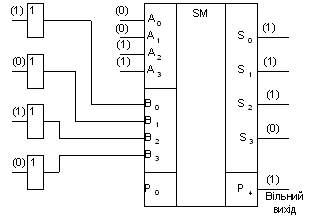
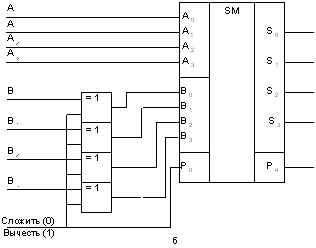
Рис. 2.32. Мікросхема К155ІМЗ у ролі віднімаючого пристрою (субтрактора) (а), у ролі сумуючого-віднімаючого пристрою(б)

Дата добавления: 2015-06-27