Двоичное дерево

Особое место в анализе цепочек формального языка занимает двоичное дерево, в состав которого входят корень и два непересекающихся двоичных поддерева, называемых левым и правым поддеревьями данного корня. В отличие от дерева разбора из корня и каждого узла дерева исходит не более двух дуг. Такое дерево оказывается более удобным для применения системы составляющих в анализе синтаксических конструкций цепочек. На рис.13 показано двоичное дерево и его два поддерева: левое поддерево, когда правое - пусто и правое поддерево, когда левое - пусто.

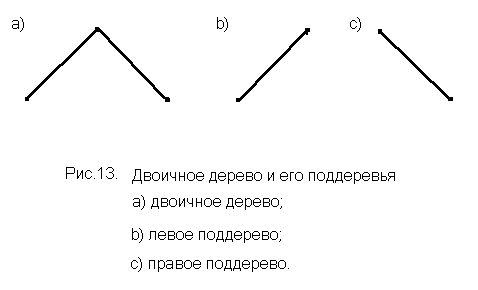
Для перехода от дерева разбора к его двоичному эквиваленту следует воспользоваться следующими правилами:

правило формирования левого поддерева: если вершина "K" является самым левым потомком вершины "J" в дереве разбора, то эта вершина формирует вершину-сток левого поддерева двоичного дерева и является левым потомком вершины "J" двоичного дерева; вершина-исток левого поддерева есть образ символа, находящегося в левой части правила грамматики, а вершина-сток - образ первого символа правой части правила грамматики;

правило формирования правого поддерева: если вершина "L" является старшим среди оставшихся (после удаления вершины "K" для формирования левого поддерева) братьев - потомков вершины "J" в дереве разбора, то эта вершина формирует вершину-сток правого поддерева двоичного дерева и является правым потомком старшего брата - вершины "K"; все последующие братья - потомки вершины "J" в дереве разбора являются правыми потомками братьев по старшинству и формируют правые поддеревья двоичного дерева; вершина-исток правого поддерева есть образ предшествующего левого символа в правой части правила, а вершина-сток - образ следующего справа символа в правой части правила

Пусть дано правило J::=KLM,

где J, K,L,M, Î VN.

На рис.14а) представлен граф двоичного дерева. В составе этого дерева - одно левое поддерево, соединяющее вершины J и K и два правых, соединяющих вершины K и L, L и M.

Пусть дано множество правил КС-грамматики:

J::= KLM, K::= k и L::= Pm,

где k,m Î V_T,

J,K,L,M,P Î V_N.

На рис. 14b) представлен граф двоичного дерева. В составе этого дерева три левых поддерева, соединяющих вершины J и K, K и k, L и P и три правых поддерева,соединяющих вершины K и L, L и M, Р и m.

Рассмотрим двоичные деревья для синтаксических деревьев и деревьев разбора, представленных в примерах 20, 21, 22 и 23.

Пример 30. Для синтаксического дерева, представленного на рис. 6, сформировать двоичное дерево.

На рис.15 представлен двоичный эквивалент дерева разбора в соответствии с правилами грамматики, заданными в примере 20.

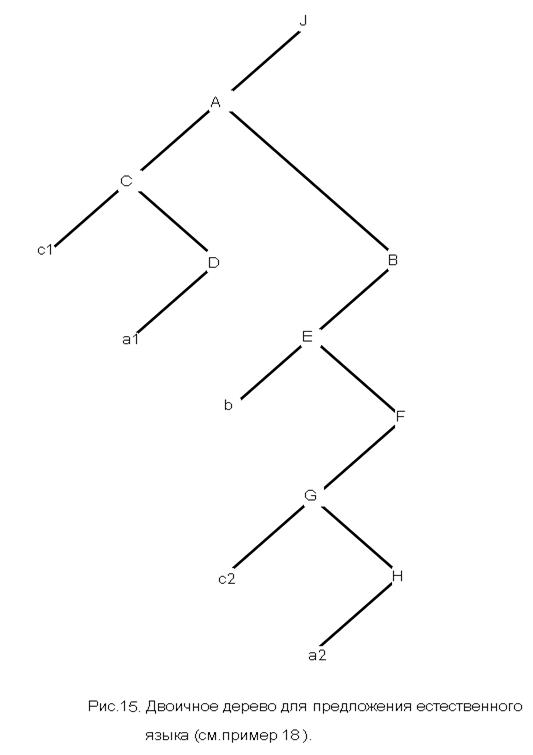
Пример 31. Для дерева разбора синтаксической переменной <программа> языка программирования Паскаль, представленного в примере 21 (рис. 7), сформировать двоичное дерево.

На рис.16 представлен двоичный эквивалент дерева разбора в соответствии с правилами грамматики, заданными в 2 (пример 1).

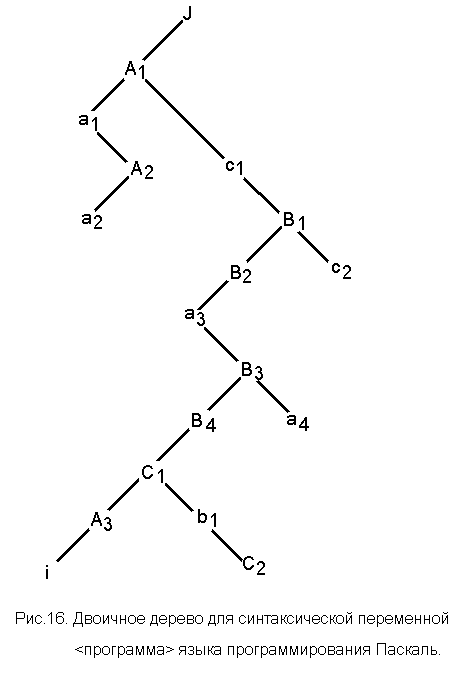
Пример 32. Для дерева разбора синтаксической переменной <выражение> языка программирования Паскаль, представленного в примере 22 (рис. 8), сформировать двоичное дерево.

На рис.17 представлен двоичный эквивалент дерева разбора в соответствии с правилами грамматики, заданными в 2 (пример 1).

Пример 33. Для синтаксических деревьев арифметических выражений:

a) J = a +b², b) J = a² + b²,

c) J = (a + b)² d)J = a x b + a(a - b)

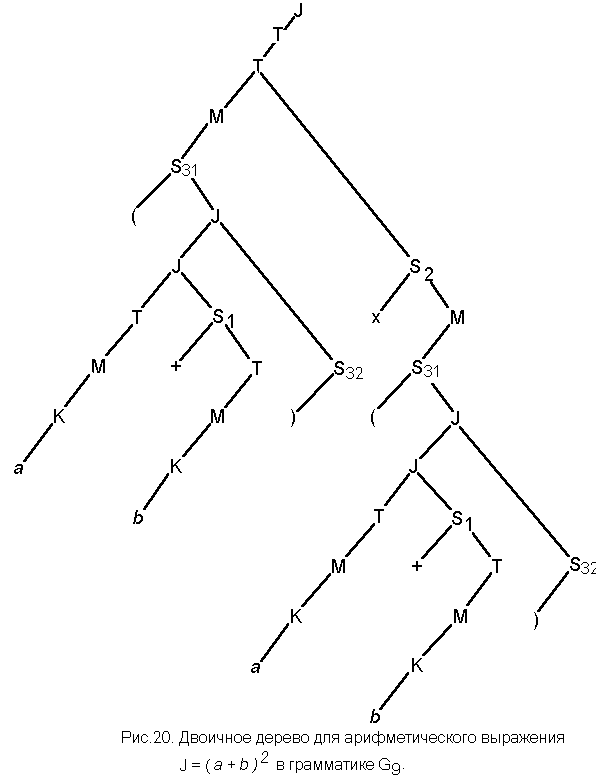
в грамматике G9, рассмотренных в примере 23 (рис. 9,10,11,12), сформировать двоичные деревья.

На рис.18, 19, 20 и 21 представлены двоичные эквиваленты синтаксических деревьев по правилам грамматики, заданными в 3 (пример 14).

Дата добавления: 2015-06-27