Свойства двоичного дерева

С первого взгляда двоичное дерево кажется гораздо менее удовлетворительным, чем дерево разбора. В дереве разбора все терминальные символы висят на концах веток, что позволяет выстроить цепочку формального языка в естественном порядке. В двоичном дереве терминальные символы равномерно распределены по дереву, что существенно затрудняет прочтение цепочки. В дереве разбора все нетерминальные символы являются узлами дерева. В двоичном дереве - нет. В двоичном дереве все левые поддеревья связывают левую часть и голову (первый символ) правой части правила грамматики, а все правые поддеревья связывают голову (первый символ) и хвост правой части правила грамматики, что существенно облегчает использование системы составляющих в разборе цепочек формального языка.

Свойства левого поддерева: последовательное соединение левых поддеревьев называют максимальным левым поддеревом; максимальное левое поддерево всегда начинается в узле, являющемся образом нетерминального символа, и заканчивается в вершине, являющейся образом терминального символа; максимальное левое поддерево, начинающееся в вершине, являющейся образом начального символа, и заканчивающееся в вершине, являющейся образом самого левого в цепочке терминального символа, называют позвоночником двоичного дерева; позвоночник двоичного дерева совпадает с левым поддеревом синтаксического дерева.

Например, максимальные левые поддеревья представляют цепочки вершин:

a) на рис. 15: {(J,A,C,c1), (B,E,b), (F,G,c2)};

b) на рис. 16: {(J,A1,a1), (B1,B2,a3), (B3,B4,C1,A3,i)};

c) на рис. 17: {(C2,C3,C4,A3,i), (C3,C4,C1,A}.

Cреди максимальных левых поддеревьев позвоночниками двоичных деревьев являются цепочки вершин:

а) на рис.15: (J,A,C,c1);

b) на рис. 16: (J,A1,a1);

c) на рис. 17: (C2,C3,C4,A3,i).

Оставшиеся максимальные левые поддеревья являются позвоночниками для поддеревьев соответствующих двоичных деревьев.

Свойства правого поддерева: последовательное соединение правых поддеревьев называют максимальным правым поддеревом; максимальное правое поддерево есть образ правой части правила; начальная вершина максимального правого поддерева есть образ головы (первого символа) правой части правила; максимальные правые поддеревья, начальные вершины которых принадлежат позвоночнику, называют ребрами двоичного дерева; позвоночник вместе с ребрами формируют скелет двоичного дерева.

Например, максимальные правые поддеревья представляют цепочки вершин:

a) на рис.15: {(A,B), (C,D), (E,F), (G,H)};

b) на рис. 16: {(A1,c1,B,c2), (a1,A2), (a3,B3,a4), (C1,b1,C2)};

c) на рис. 17:{(C3,D1,C3), (C4,D2,C4)}.

Cреди максимальных правых поддеревьев ребрами двоичных деревьев являются цепочки вершин:

a) на рис. 15: (A,B) и (C,D);

b) на рис.16: (A1,c!,B,c2) и (a1,A2);

c) на рис. 17: (C3,D1,C3) и (С4,D2,C4).

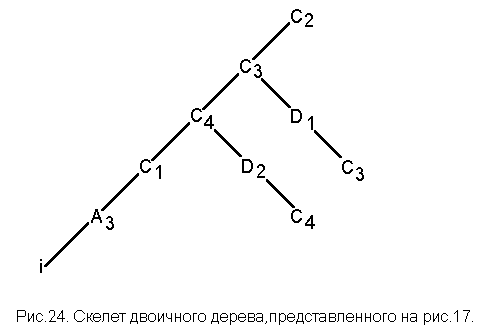
На рис.22, рис.23 и рис.24 приведены скелеты двоичных деревьев, изображенных на рис.15, рис.16 и рис.17

Каждая вершина двоичного дерева расположена либо на скелете, либо на поддеревьях, нисходящих влево от вершин, принадлежащих максимальным правым поддеревьям. В свою очередь, для каждого поддерева, нисходящего влево от вершины, принадлежащей максимальному правому поддереву, может быть найден свой позвоночник и свой скелет. Поэтому получение скелета является первым шагом для построения полного двоичного дерева. Для каждой правильной цепочки формального языка существует единственный скелет двоичного дерева и множество скелетов его поддеревьев. Для облегчения поиска скелетов рекомендуется индексировать правила грамматики (7) в порядке их следования в скелете сверху-вниз, т.е.

рi: ai::= bi..

Тогда номер правила грамматики, соответствующий ребру скелета, указывает на порядок его использования в разборе цепочки формального языка.

Последовательность номеров правил грамматики, соответствующих скелету называется индексом скелета.

Имя первого символа правой части используемого правила и индекс ребра скелета двоичного дерева формируют элемент системы составляющих.

Например, для дерева, представленного по правилам примера 14 на рис. 18, индексом основного скелета будет (1₁), для дерева, представленного на рис.19, - (1₁,2₁), для дерева, представленного на рис. 20, - (2₁,3₂) и, наконец, для дерева, представленного на рис. 21,- (1₁,2₁).

Существует много алгоритмов анализа цепочек формального языка при обходе вершин двоичного дерева сверху-вниз и снизу-вверх. Для объяснения их работы чаще всего используют матрицу связей и таблицу подстановок.

Матрицу связей представляет логическая функция двух переменных, описывающая наличие левых поддеревьев двоичного дерева:

ì true, если существует левое поддерево;

P(Ai;wi)= í (26)

î false, если нет такого поддерева,

где Ai - нетерминальный символ левой части правила, т.е. Ai ÎVn;

wi- первый символ правой части правила,т.е. wiÎV.

Матрицу связей удобно представить списком, как показано таблицей 1 или матрицей смежности, строки которой - символы левой части правила, столбцы - первый символ правой части правила, а элементы - значения 0 или 1,что соответствует значениям false или true логической функции P(Ai;wi).

Таблица 1

Номер правила	(символ левой части, первый символ правой части)
	(А1, w1)
	(А2, w2)
...	...

Матрица связей позволяет найти максимальные левые поддеревья, определить позвоночник и указать индекс скелета.

Таблицу подстановок представляет также логическая функция двух переменных, описывающая наличие максимальных правых поддеревьев

ì true, если существует правое поддерево;

P(i;bi\wi)= í (27)

î false, если нет такого поддерева,

где i -номер правила, для которого дается описание хвоста правой части правила;

bi\wi - хвост правой части правила, первый символ которой wi принадлежит матрице связей.

Таблица подстановок представляет множество максимальных правых поддеревьев и хранит корни всех левых поддеревьев. Связь таблицы с матрицей выполняется по номеру правила. Таблицу подстановок удобно изобразить так, как показано на таблице 2.

Таблица 2

Номер правила	(хвост правой части правила)
	(b1\w1)
	(b2\w2)
...	...

Дата добавления: 2015-06-27