Традиционная логика

Классификация и определение логик, алгебр, исчислений, теорий.

Основы математической логики

Термин логика происходит от греческого слова logos, что значит мысль, слово, разум, закономерность, и используется как для обозначения совокупности правил, которым подчиняется процесс мышления, отражающий действительность, так и для обозначения науки о правилах рассуждения и тех формах, в которых она осуществляется.

За время своего развития в математике было введено громадное количество различных понятий и определений, отражающих представления их авторов о наиболее истинном математическом описании реальной действительности или о единственно верном решении возникающих математических проблем. К наиболее фундаментальным определениям следует отнести понятия: логика, алгебра, исчисление, и теория. Анализ содержания этих понятий, установление их взаимосвязей, определение исторической последовательности введения этих понятий позволяет увидеть конечные цели введения той или иной математической абстракции. Здесь предлагается одна из возможных схем классификации этих понятий. (Схема 1)

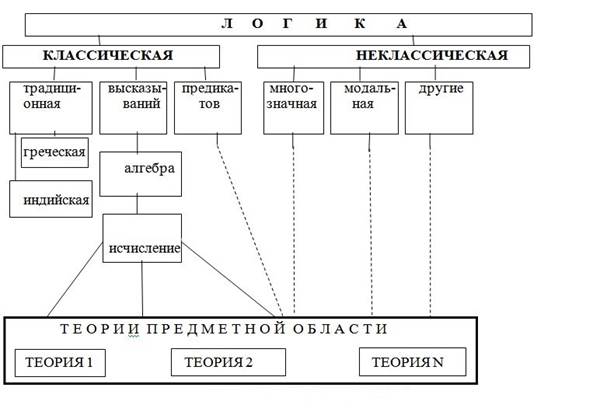
Схема 1. Классификация логики

Первоначально логика зародилась и развивалась в недрах философии единой нерасчленённой науки, которая объединяла всю совокупность знаний об объективном мире и о самом человеке и его мышлении. В традиционной логике законы и формы правильного мышления изучались в рамках ораторского искусства- одного из средств воздействия на умы людей, убеждения их в целесообразности того или иного поведения. Так было в Древней Греции, Древней Индии, Древнем Китае, Древнем Риме, средневековой России. Но в искусстве красноречия логический момент выступает ещё как подчинённый, поскольку логические приёмы служат не столько цели достижения истины, сколько цели убеждения аудитории.

Развитие науки логики на протяжении ряда столетий протекало по двум направлениям. Одно из них начиналось с древнегреческой логики (в особенности с логики Аристотеля), на основе которой развивалась логика в Древнем Риме, затем в Византии, Грузии, Армении, арабоязычных странах Ближнего Востока, в Западной Европе и России. Другое направление имело своим истоком индийскую логику, на основе которой развивалась логика в Китае, Тибете, Монголии, Корее, Японии, Индонезии, на Цейлоне.

Содержание традиционной логики соответствует первому этапу развития формальной логики. Необходимо отметить, что переходной фазой ко второму этапу является введение в традиционной логике понятия высказывание и разработка правил вывода применимых к высказываниям.

Второй этап - это появление математической (или символической) логики. Немецкий философ Г.В. Лейбниц (1646-1716) по праву считается основоположником этого этапа. Начиная с Лейбница, в логике используется в качестве метода исследования метод формализации, который традиционная логика относила только к методам математического исследования, а Лейбниц показал, что он имеет общенаучный характер. Лейбниц пытался построить универсальный язык, с помощью которого споры между людьми можно было разрешать посредством вычислений. В XIX в. математическая логика получила интенсивное развитие в работах Д. Буля (разработка алгебры высказываний), Э. Шрёдера (введение понятия логического исчисления), Г. Фреге (создание логики предикатов). Со времени своего возникновения и до двадцатых годов XX в. логика преимущественно развивалась в направлении формализации каталогизирования правильных способов рассуждений в пределах двух значений истинности. Суждения могли быть либо истинными, либо ложными. Такая логика именовалась классической или двузначной.

Третий этап развития математической логики связан с созданием неклассических логик, которые оперируют либо бесконечным множеством значений истинности, либо конструктивными (по сравнению с классической логикой) методами доказательства истинности суждений, либо модальными суждениями, либо исключают отрицания, имеющиеся в классической логике. В многозначных логиках число значений истинности аргументов и функций может быть любым конечным и даже бесконечным числом. К наиболее известным в этой области можно отнести работы Я. Лукасевича (введение трёхзначной системы), Гейтинга (введение трёхзначной системы с новыми операциями отрицания и импликации), Д.А.Бочвара (введение трёхзначной логики с целью разрешения парадоксов классической математической логики методом формального доказательства бессмысленности определённых высказываний), Г. Рейхенбаха (введение трёхзначной логики для описания явлений квантовой механики), Поста (введение n - значной логики). Развитие многозначных логик подтверждает мысль, что истина всегда конкретна, а также положение об относительном характере конкретно-научных знаний: то, что является тождественно-истинным в одной логической системе, не оказывается тождественно-истинным в другой. В классической двузначной логике рассматривались простые и сложные ассерторические суждения, т.е. такие, в которых не установлен характер связи между субъектом и предикатом.

Например: “Морская вода - солёная” или “Дождь то начинал хлестать тёплыми крупными каплями, то переставал”. В модальных суждениях раскрывается характер связи между субъектом и предикатом или между отдельными простыми суждениями в сложном модальном суждении. Например: “Необходимо соблюдать правила уличного движения” или “Если будет дуть попутный ветер, то, возможно, мы приплывём в гавань до наступления темноты”. Модальными являются суждения, которые включают модальные операторы (модальные понятия), т.е. слова “необходимо”, “хорошо”, “возможно”, “невозможно”, “случайно”, “запрещено” и многие другие. Модальные суждения рас-сматриваются в специальном направлении неклассической логики - в мо-дальной логике. Возникновение модальной логики как системы связано с именем американского логика и философа К.И. Льюиса. В этом направлении известны работы Ф.В. Аккермана и Р. Фейса. Интересна интерпретация модальных логик. Известный австрийский философ и логик Р. Карнап пытался интерпретировать модальные понятия с помощью, так называемой теории “возможных миров”, в которой допускается наличие множества “миров”, один из которых - действительный, реальный мир, а остальные - возможные миры. Необходимым объявляется то, что существует во всех мирах, возможным - то, что существует хотя бы в одном. К другим логикам можно отнести: интуиционистскую (Л. Брауэр, Гейтинг), конструктивную (А.Н. Колмогоров, В.И. Гливенко, А.А. Марков), паранепротиворечивую (С. Яськовский, Ньютон да Коста). Вообще, к настоящему времени, известно более семидесяти логик, соответствующих различным философским идеям и лежащих в основе решения множества научно-технических задач.

Для каждой из логик может быть построена своя алгебра. Содержанием этой алгебры являются операции над элементами данной логики: высказываниями, предикатами, модальными операторами и т.д. Эти алгебры могут отличаться друг от друга набором и определением операций над элементами логики. Также для каждой логики может быть создано своё исчисление, которое строится по схеме: алфавит, правила образования формул, правила преобразования (вывода). Формулы образуются из элементов логики с использованием операций соответствующей алгебры, правила преобразования (вывода) позволяют определить истинность конкретной формулы в данном исчислении. В более широком смысле любое исчисление является математической моделью процесса перехода от посылок к следствию, проводимого по определённым правилам вывода.

Для того чтобы использовать методы той или иной логики применительно к конкретной области знаний (предметной области) необходимо построить соответствующую теорию, состоящую из набора аксиом. Если теория адекватно описывает заданную предметную область, то все факты из этой области являющиеся истинными, будут следствиями аксиом этой теории, а ни один факт, являющийся ложным, не будет следствием данных аксиом. Адекватно построенная теория позволяет проверять те или иные гипотезы из данной предметной области формальным образом, что является математической основой решения конкретных практических в этой области знаний. Подробнее о методах построения теории в предметной области, т.е. онтологии и её практи-ческом использовании в лекции 11.

Основным представителем древнегреческой традиционной логики, является Аристотель (384-322 до н.э.). Аристотель попытался ввести в научную систему способы, с помощью которых можно наиболее эффективным образом постигать истину в разумной полемике. При описании логики Аристотеля вводится понятие суждение, обозначающее законченную мысль, которую можно выразить при помощи простого выражения естественного языка. Аристотель сформулировал следующих три закона традиционной логики, устанавливающих правила использования суждений в полемике.

1.Тождественность «А является А»

(некоторая вещь всегда равна самой себе; суждение означает само себя)

2.Противоречие «А не является не - А».

(вещь не может одновременно обладать и не обладать некоторым свойством; никакое суждение не является одновременно истинным и ложным)

3.Исключение третьего «А не является одновременно и А, и не – А»

(вещь либо обладает, либо не обладает некоторым свойством; каждое суждение либо истинно, либо ложно)

Согласно Аристотелю суждение состоит из четырех элементов: квантор, субъект, связка, предикат.

Пример: в суждении “Все русские являются любителями кваса”

“ русские” - это субъект, “все”- это квантор, “любители кваса”- это предикат, а “являются”- связка.

В традиционной логике допускаются четыре формы суждений, каждая из которых характеризует возможное отношение между классом субъектов (S) и классом предикатов (P).

· все S являются P;

· никакой из S не является P;

· некоторые из S являются P;

· некоторые из S не являются P.

Силлогизм-это множество правил, определяющих то, какие верные умозаключения могут быть получены из множества суждений, каждое из которых записано в одной из допустимых форм.

Пример: заданы два суждения в одной из допустимых форм:

“Все русские являются любителями кваса” (1)

“Все москвичи - русские” (2)

на основе силлогизма может быть получено корректное умозаключение:

“Все москвичи являются любителями кваса”

Таким образом, с самого зарождения логики основным вопросом этой науки был вопрос построения логического вывода из известных предпосылок. Каждое правило силлогизма определяет переход от предпосылок к умозаключению, являющемуся интуитивно очевидным. Если сложная дискуссия состоит из многих дедуктивных шагов, то вся она будет логически правильной в том случае, если каждый ее шаг можно объяснить при помощи силлогического правила.

Недостатки силлогизма являются, прежде всего, следствием канонизации основных четырех форм суждений. Все допустимые суждения касаются отношений между классами, т.е. силлогизм – это, прежде всего логика класса.

В предыдущем примере процесс вывода можно выполнить только тогда, когда класс предикатов одного суждения (“русские” в выражении 2) согласуется с классом субъектов другого суждения (“русские” в выражении 1).

Все силлогические правила основываются на заранее выполняемом свойстве транзитивности операции включения в состав класса, т.е. если класс A входит в состав класса B, а класс В входит в состав класса С, то класс А должен входить в состав класса С. Если это свойство нарушено, то умозаключение может быть неверным.

Например: “Все русские живут в России” (1)

“Некоторые русские живут в Нью-Йорке” (2)

“Нью-Йорк находится в России” (3)

В этом примере 3-е умозаключение неверно, т.к. “русские” из 1-ой предпосылки и “русские” из 2-ой предпосылки принадлежат разным классам. Для преодоления этого недостатка ученики Аристотеля выделили принципы дедуктивного вывода для более мелкого элемента логических рассуждений-высказываний.

Высказывание - это любое суждение, которому можно приписать истинностное значение (либо истина, либо ложь). Высказывание - это более общее понятие, чем суждение в силлогизме.

Например, выражение: “Слон Y существует”- является высказыванием, но не силлогическим суждением, так как оно не соответствует ни одной из четырёх приведённых выше форм суждений. Для решения основного вопроса логики, применительно к высказываниям (доказательство их истинности), последователями Аристотеля были получены правила дедуктивного вывода для высказываний (таблица 4).

Таблица 4

Латинское название правила вывода.	Правила вывода.
Modus Ponendo Ponens	Если из P следует Q и P истинно, то и Q истинно.
Modus Tollendo Tollens	Если из P следует Q и Q ложно, то и P ложно.
Modus Ponendo Tolles	Если P и Q не могут одновременно быть истинными и P истинно, то Q ложно (исключающее “ИЛИ”)
Modus Tollendo Ponens	Если либо P, либо Q является истин- ным и P не истинно, то Q истинно (включающее “ИЛИ”).

Данные правила представляют собой гораздо более общий метод вывода, чем исходный силлогизм. Они являются первым шагом к созданию логики высказываний. Такая логика была полностью разработана лишь в XIX вв.

Индийская логика развивалась на протяжении двух тысячелетий, и история её развития на мировом уровне ещё до конца не изучена. Хотя библиография по индийской философии и логике огромна, единства во взглядах на ход её развития не достигнуто. В индийской логике много внимания уделяется теории умозаключения, которое в ней отождествляется с доказательством. Существовавший первоначально взгляд, что силлогизм состоит из десяти суждений (членов), меняется. Развитие логики шло по пути сокращения членов силлогизма до пяти: 1)тезис, 2)основание, 3)пример, 4)применение и 5)вывод. Эта система силлогизма стала господствующей в индийской логике. Особенностями индийской логики являются следующие:

1. оригинальное учение о пятичленном силлогизме, в котором важна мысль о неразрывной связи дедукции и индукции;

2. суждение не признается самостоятельным актом мысли, а рассматривается как член умозаключения;

3. восприятие не есть нечто непосредственно данное, а заключает в себе акт “суждения-умозаключения”. Иными словами, в основе наших восприятий лежит приобретённый нами опыт;

4. различение вещи “в себе” (т.е. внутренний речи, являющейся формой процесса мышления, когда человек как бы ведёт разговор с самим собой) и речи “для других” (т.е. внешней речи, когда происходит передача мыслей и общение людей в устной или письменной форме).

Первая характеризуется более сокращённым способом мышления, чем вторая. Следует отметить, что европейская психология лишь в XX в. приступила к изучению этих видов речи и установлению различий между ними. Хотя индийская логика так и не пришла к использованию символов, что и ограничило её дальнейшее развитие, она уникальна и самобытна она возникла раньше и развивалась независимо от древнегреческой. С греческой философией и логикой Индия познакомилась лишь в результате похода Александра Македонского (356-323г. до н.э.)

Дата добавления: 2015-06-27