T(a,b) (4)

Y(b) (3)

T(a,b) (4)

Y(b) (3)

T(a,b) (4)

Y(b) (3)

T(a,b) (4)

Y(b) (3)

T(a,b) (4)

Y(b) (3)

J(b,c) (2)

Так как теория представляет из себя систему аксиом, связанных знаком “конъюнкция”, то (1) и (2) представляет из себя следующее выражение: ù J(b,c) ÙJ(b,c), которое всегда ложно и следовательно эта теория противоречива. Если дизъюнкты (1) и (2) резольвируются друг с другом, то получающаяся

резольвента называется пустым дизъюнктом. Таким образом вывод пустой дизъюнкты свидетельствует о пртиворечивости данной теории.

Алгоритм, позволяющий автоматизировать процесс доказательства теорем на основе правила резолюции, состоит из следующих шагов:

1. Добавление к системе аксиом дизъюнкта, являющегося отрицанием доказуемой теоремы.

2. Поиск среди дизъюнкт (аксиом) теории для добавленной дизъюнкты резольвируемой с ней второй родительской дизъюнкты.

3.Унификация переменных.

4.Выполнение правила резолюции и формирование резольвенты.

5.Если резольвента пустая, то теорема доказана и окончание работы алгоритма, если нет - присоединение резольвенты в виде новой дизъюнкты к существующей системе дизъюнкт (аксиом) теории и переход к шагу 2.

Пример: Пусть имеется некоторая теория, состоящая из следующих аксиом (дизъюнкт):

R(a) Ú ù J(a,b) (1)

J(x,y) Ú ù T(x,y) (2)

Необходимо доказать, что утверждение R(a) (5) является следствием данной теории.

Доказательство проведём в соответствии с предложенным алгоритмом.

Шаг 1. Добавим отрицание доказуемого утверждения к системе аксиом теории и получим новую систему аксиом:

R(a) Ú ù J(a,b) (1)

J(x,y) Ú ù T(x,y) (2)

ù R(a) (5)

Шаг 2. Дизъюнкты (1) и (5) являются родительскими.

Шаг 3. У родительских дизъюнкт аргументы унифицированы.

Шаг 4. Выполняя правило резолюции, получаем следующую резольвенту :ù J(a,b) (6).

Шаг 5. Резольвента не пустая, следовательно, присоединяем её к существующей системе аксиом, получаем новый набор аксиом и переходим к шагу 2.

R(a) Ú ù J(a,b) (1)

J(x,y) Ú ù T(x,y) (2)

ù R(a) (5)

ù J(a,b) (6)

Шаг 2. Две резольвенты (2) и (6) являются родительскими.

Шаг 3. Проводя унификацию переменных в родительских дизъюнктах, получим следующую систему аксиом:

R(a) Ú ù J(a,b) (1)

J(a,b) Ú ù T(a,b) (2)

ù R(a) (5)

ù J(a,b) (6)

Шаг 4. Выполняя правило резолюции, получим следующую резольвенту: ù T(a,b) (7).

Шаг 5. Резольвента не пустая, следовательно присоединяем её к существующей системе аксиом, получаем новый набор аксиом и переходим к шагу 2.

R(a) Ú ù J(a,b) (1)

J(x,y) Ú ù T(x,y) (2)

ù R(a) (5)

ù J(a,b) (6)

ù T(a,b) (7)

Шаг 2. Две резольвенты (4) и (7) являются родительскими.

Шаг 3. У родительских дизъюнкт аргументы унифицированы.

Шаг 4. Выполняя правило резолюции, получаем пустую резольвенту.

Шаг 5. Резольвента пустая, следовательно утверждение доказано и алгоритм заканчивает свою работу.

Отличия в различных алгоритмах, реализующих правило резолюции заключаются в основном в различии стратегии поиска родительских дизъюнкт.

ПРИМЕР:

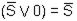
F₁ = C₁ ^ C₂ ^ C₃ ^ C₄

Проблема: Каким образом строить поиск пустой резольвенты.

А) C₁ и C₄ C₅ =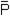

Б) C₂ и C₃ C₆ = Р

В) C₅ и C₆ C₇ = (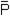 Ú 0) Ù (РÚ 0) = (0 Ù 0) пустая резольвента.

Значит F₁ противоречиво.

Если F₁ истина, то остановкой для алгоритма является отсутствие пар родительских предложений.

В случае использования предикатов, когда аргументом может быть переменная и константа, необходимо найти такие значения переменной, при которых данная формула F₁ будет противоречива. Такая подстановка (константы вместо переменных) называется унификацией.

ПРИМЕР:

x, y, z, t, v – переменные.

a, b, c – константы.

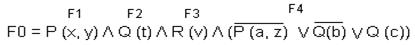
А) F₁ и F₄ S₁ = {x / a, y / z};

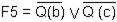
Б) F₂ и F₄ S₂= {t / b};

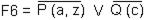
B) F₂ и F₄ S₃= {t / c};

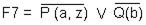
Г) F₂ и F₅ S₄= {t / b};

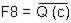
Д) F₂ и F₈ S₅= {t / с};

F₉ = пусто

Проблема: Чтобы использовать «Пролог» и доказательства, необходимо сформулировать исходные аксиомы и выходное целевое выражение в виде произведения дизъюнкт Хорна.

ПРИМЕР: Пусть высказаны следующие утверждения:

1. Кто может читать, тот грамотный.

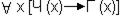
2. Дельфины не грамотны.

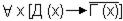
3. Некоторые дельфины обладают интеллектом.

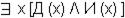
4. Некоторые из тех, кто обладает интеллектом не могут читать.

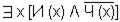Необходимо доказать.

Общее выражение имеет вид:

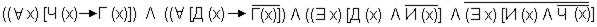исправить И(Х) без отрицания.

После преобразований (исключения кванторов, введения сколемовской переменной, исключения связок импликации, введения новых переменных) получаем следующую систему предложений:

1.

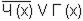
2.

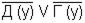
3. а) Д (А)

б) И (А)

А – сколемовская переменная.

Отрицание утверждения, которое нужно доказать, имеет вид:

4.*

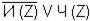
Одно из возможных доказательств создает следующую последовательность резольвент:

5. Ч(А) резольвента из 3 б) и 4*, и замена Z на A.

6. Г(А) резольвента из 5 и 1, и замена Х на A.

7. 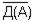резольвента из 6 и 2, и замена У на A.

8. Пустая резольвента из 7 и 3 а).

Данный вывод можно представить в виде графа вывода. Вершины графа помечены предложениями. Когда два предложения C_i и C_j создают резольвенту r_ij, то мы образуем новую вершину, помеченную r_ij, причем ребра связаны с вершинами C_i и C_j.

C_i и C_j - Родители для r_ij

r_ij - является потомком C_i и C_j

Опровержение на основе резолюций может быть представлено деревом опровержения, корневая вершина которого помечена предложением NIL.

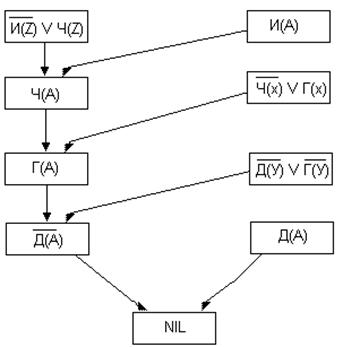
Рис.12. Стратегии поиска родительских предложений

Дата добавления: 2015-06-27