Рассчет средней величины лучевой скорости звезды и среднеквадратичной ошибки

Линий в спектре звезды.

Измерение положений спектральных линий в спектре звезды и определение их смещений относительно соответствующих

В соответствии с законом Доплера-Физо - V_л= СΔλ/λ, для определения лучевой скорости мы должны измерить Δλ - смещение какой-либо спектральной линии в спектре звезды относительно линии c такой же длинной волны в спектре сравнения.

Понятно, что Δλ должна быть измерена в тех же самых единицах, что и λ, т.е. не в миллиметрах, а в ангстремах.

Мы будем определять величину такого смещения не для одной линии, а для всех отождествлённых линий в спектре звезды.

Сначала эти смещения определяют в миллиметрах. Для этого измеряют расстояния L _звезды от того же самого “нуль пункта” до середины каждой из отождествлённых линиий в спектре звезды. Здесь важно придерживаться той же методики и такой же точности, что и в случае проведения измерений на спектре сравнения

Напоминаю, что расстояние до линий спектра сравнения - L _сравн. - мы уже измеряли раньше. Разница между измеренными величинами для одной и той же спектральной линии даст нам величину |ΔL_i| = L _звезды - L _{сравн .} смещения линии с какой-то длиной волны в спектре звезды относительно линиии с такой же длиной волны в спектре сравнения в мм. Находится абсолютная величина ΔL_i, так как знак лучевой скорости определяется только по направлению движения звездыотносительно наблюдаталя (см. начало инструкции).

Если найденное смещение - ΔL_i (мм.) умножить на величину дисперсии – D (Å/мм.), то мы найдем смещение одной линии спектра звезды относительно линии с такой же длиной волны в спектре сравнения - Δλ_i (Å)

Δλ_i=D × ΔL_i

Понятно, что в спектре звезды Вы будете измерять Δλ_i для всех отждествлённых линий спектра звезды. Результаты определения ΔL_i и Δλ_i заносятся в 4 и 5 столбцы таблицы 1.

По найденным значениям Δλ_i опираясь на формулу Доплера-Физо

V_л=С × Δλ/λ

рассчитаем V_i - лучевые скорости звезды, определённые по всем спектральным линиям, отождествлённым в спектре звезды. Напоминаю, что при определении значений лучевых скоростей, обязательно учитывают направление смещения спектральных линий, а значит, и знак лучевой скорости звезды. Напоминаю, что лучевая скорость считается положительной если звезда движется от Солнца и спектральные линии в её спектре смещены в область больших длин волн. В противном случае лучевая скорость отрицательна. Все дальнейшие расчёты следует проводить с учётом знака лучевой скорости.

По найденным значениям лучевых скоростей V_i находится среднее арифметическое значение - V_ср – лучевой скорости звезды.

V _ср=ΣV_i/n

Где:

n - число найденных значений лучевой скорости,

ΣV_i - сумма всех найденных значений лучевых скоростей.

Точность полученного результата оценим среднеквадратичной ошибкой:

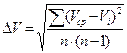
Внимание! Лучевые скорости и среднеквадратичную ошибку измерений достаточно считать с точностью до км/с. Не нужно рассчитывать их значения с точностью до м/с. Средняя лучевая скорость и среднеквадратичная ошибка измерений заносятся в 7 и 8 столбцы таблицы 1.

6. Учёт орбитального движения Земли.

Мы нашли значение средней лучевой скорости звезды относительно наблюдателя в день фотографирования её спектра. Это значение не характерно для звезды, так как содержит проекцию орбитальной скорости Земли на направление к звезде. Орбитальная скорость движения Земли около 30 км/c. По порядку величины сравнима с лучевой скоростью звезды, именно поэтому лучевые скорость звёзд измеряют относительно Солнца, а не Земли. Полученное значение лучевой скорости звезды необходимо исправить за движение Земли и вычислить лучевую скорость звезды относительно Солнца. Можно показать, что это можно сделать используя соотношение:

V_© = V_ср. – 29,8_*sin(λ_{зв. –} λ_с.)_*cos(β_зв.)

Здесь:

V_© – лучевая скорость звезды относительно Солнца.

Определение этой величины является целью данной работы.

29,8 - средняя орбитальная скорость движения Земли (км/с);

V_{ср – найденное нами выше среднее значение лучевой скоро звезды;}

λ _зв. - геоцентрическая эклиптическая долгота звезды;

β зв. - геоцентрическая эклиптическая широта звезды;

λ _с. - геоцентрическая долгота Солнца в день фотографирования спектра звезды.

Значения λ_зв. И βзв. звезды рассчитываются по известным экваториальным координатам звезды, которые приведены на выданном Вам планшете со спектрограммами. При этом используются следующие соотношения:

sin (β_зв.)= sin(δ)_*cos(ε) - cos(δ)_*sin(α)_*sin(ε)

cos(β_зв.)_*cos(λ_зв.)=cos(δ)_*cos(α)

cos(β_зв.)_*sin(λ_зв.)= sin(δ)_*sin(ε) + cos(δ)_*sin(α)_*cos(ε)

где:

ε = 3° 27' = 23,45^о - наклонение небесного экватора к эклиптике;

α и δ - экваториальные координаты звезды, причём α должна быть выражена в градусной мере.

β_{зв. -} геоцентрическая эклиптическая широта звезды;

λ_{зв. -} геоцентрическая эклиптическая долгота звезды;

Решение этой системы начинается с первого уравнения, которое позволяет сразу определить геоцентрическую эклиптическую широту звезды β зв.

Подставляя найденное её значение во второе уравнение, находим два значения второй координаты звезды - λ_зв. - её геоцентрической эклиптической долготы. Одно значение выдаст Вам калькулятор, а второе значение Вы определяете сами, зная, что косинус имеет одинаковые по величине и знаку значения в двух четвертях. Необходимо выбрать нужное значение. Для этого используют третье уравнение. Определяя из него знак синуса λ_зв, находим в какой четверти лежит верное решение.

Очень просто можно определить λ_{с ..} Геоцентрическая долгота Солнца в градусах, с удовлетворительной для наших целей точностью, численно равняется числу полных суток, прошедших с даты 21 марта до даты фотографирования спектра.

Дата фотографирования напечатана на выданном Вам листке со спектрограммой.

Результаты вычислений занесите в таблицу 3.

Таблица 3

α	δ	Cos(βзв.)	β^озв.	Cos(λзв.)	Sin(λзв.)	λ^озв.	λ с^о	V© (км\сек)

Таким образом, учёт орбитального движения Земли позволяет получить значение лучевой скорости звезды относительно Солнца. Окончательно результат записываем в виде:

V = V_© ± ΔV

Примечание. Цель нашей работы не столько определить точное значение лучевой скорости какой-то звезды, как понять методику её определения. Вы должны знать, что реальные пространственные (и лучевые) скорости звёзд имеют порядок нескольких десятков (редко до сотен) км/с. Мы выполняли все измерения на не подлинных спектрограммах звезды, а на искусственно начерченных. Это сделано по следующим соображениям: во-первых, подлинные спектрограммы звёзд (см. «Лабораторный практикум по курсу общей астрономии» М.М.Дагаева) довольно низкого качества и, во-вторых, и это главное, наш измерительный инструмент (линейка) не позволяет выявить разницу в величинах смещений «красных» и «синих» линий. Эта разница меньше точности (0,2-0,3 мм.) наших измерений. Для проведения качественных измерений таких спектрограмм нужен другой измерительный инструмент – измерительный микроскоп. Измерять такие спектрограммы с помощью простой линейки лишено всякого смысла – величина смещения всех линий спектра звезды относительно линий спектра сравнения будет практически одинаковой.

Дата добавления: 2015-06-27