Основы теории и расчетные формулы

Цель работы

Изучение теплопередачи от потока жидкости в трубе круглого сечения к воздуху в окружающей среде

Лабораторная работа 8

ПРЕДЛАГАТЬ БОЛЬШЕ ТОГО, ЧТО ВЫ ПРОДАЕТЕ 195

Прием 83. ЛИШНЕЕ ЯЙЦО В КОКТЕЙЛЬ..... 196

Прием 84. ПРОДАВЕЦ В РОЛИ СОВЕТЧИКА.... 198 Прием 85. ВОПРОС НЬЮ-ЙОРКСКОГО СТОЛА

ЗАКАЗОВ................ 200

Прием 86. ПРЕДЛАГАЙТЕ ЧУТЬ БОЛЬШЕ..... 202

Прием 87. ПОВЫШАЙТЕ, А НЕ ПОНИЖАЙТЕ... 204 Прием 88. НАЙДИТЕ ДЕЙСТВЕННЫЕ СРЕДСТВА

ПОКАЗАТЬ ИЗДЕЛИЕ.......... 206

Прием 89. ПРЕДЛАГАЙТЕ ПРЕМИЮ, КОТОРАЯ

ПРИВЯЖЕТ К ВАМ КЛИЕНТА..... 210

Прием 90. ПРИНИМАЙТЕ ПЛАСТИКОВЫЕ ДЕНЬГИ 213

Прием 91. ПРЕДЛАГАЙТЕ ПРЕМИЮ........ 215

СОДЕРЖАНИЕ

Прием 92. УВЕЛИЧИВАЙТЕ ВРЕМЯ, КОГДА ВЫ

ОТКРЫТЫ............... 217

Прием 93. ПРЕДЛАГАЙТЕ “ЛИДЕРА ЗАТРАТ”.. 218

Прием 94. ПРЕДЛАГАЙТЕ СОПУТСТВУЮЩИЕ

ТОВАРЫ................ 219

Прием 95. ПРЕДЛОЖИТЕ ТЕЛЕФОННЫЕ ЗАКАЗЫ

И ПОСКОРЕЕ!............. 221

Прием 96. НЕ ЖДИТЕ, КОГДА ПРИМУТ БЮДЖЕТ 224 Прием 97. ДАВАЙТЕ ВРЕМЯ НА РАЗДУМЬЕ... 225 Прием 98. БОРОТЬСЯ ЗА ПРАВО ПОЛУЧИТЬ... 226 Прием 99. ДАВАЙТЕ ПРЕМИЮ ТЕМ, КТО ПРИВО­ ДИТ К ВАМ КЛИЕНТА........ 228

Прием 100. СПРАШИВАЙТЕ ДРУГИХ, КАК ОНИ

РАЗВИВАЮТ БИЗНЕС......... 229

Прием 101. ОБНАЛИЧИВАЙТЕ ЧЕКИ....... 231

Определение средних (по поверхности трубы) коэффициентов теплоотдачи от жидкости к внутренней поверхности трубы и от внешней поверхности трубы к окружающему воздуху, а также среднего коэффициента теплопередачи от жидкости к воздуху через гладкую и ребристую стенки при ламинарном течении жидкости в трубе круглого сечения в условиях естественной конвекции окружающего воздуха.

Процесс теплообмена между текучей средой и твердым телом, происходящий на поверхности твердого тела, называется теплоотдачей. Как правило, теплоотдача осуществляется конвективными механизмами, т.е. вследствие движения макрообъемов текучей среды. При этом важную роль в процессе конвективной теплоотдачи играет и перенос тепла молекулярными механизмами (теплопроводность). Практический интерес представляет расчет теплового потока Q, Вт, передаваемого от жидкости к поверхности твердого тела (или наоборот). Эта величина описывается достаточно простой формулой, называемой формулой Ньютона–Рихмана

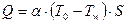, (8.1)

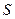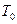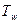где – площадь поверхности теплообмена, м²; и – температуры текучей среды и поверхности, соответственно, К; 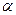– коэффициент теплоотдачи, Вт/(м²×К), характеризующий интенсивность этого процесса. Таким образом, для расчета величины теплового потока между жидкостью и поверхностью твердого тела необходимо найти коэффициент теплоотдачи. Это возможно либо расчетным, либо экспериментальным путем.

Расчетный подход основан на использовании критериальных соотношений, полученных в результате приближенного аналитического решения задачи теплообмена или статистической обработки экспериментальных данных. Принято различать вынужденную конвекцию (при которой причина движения среды является внешней по отношению к рассматриваемому процессу теплообмена) и свободную (естественную) конвекцию, при которой сам процесс теплообмена является причиной движения текучей среды. В обоих случаях решение задачи теплоотдачи может быть получено в виде зависимости безразмерного коэффициента теплоотдачи – так называемого критерия Нуссельта – от других безразмерных параметров и аргументов. Причем в случае вынужденной конвекции эта зависимость обычно имеет вид

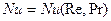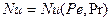или (8.2)

а при свободной конвекции –

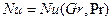(8.3)

Критерии, фигурирующие в выражениях (8.2) и (8.3), имеют следующие значения

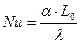– число Нуссельта (безразмерный коэффициент теплоотдачи);

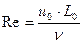– число Рейнольдса (отношение интенсивностей конвективного и молекулярного переноса импульса);

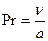– число Прандтля(отношение интенсивностей молекулярного переноса импульса и теплоты);

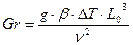– критерий Грасгофа (отношение произведения силы инерции и архимедовой силы к квадрату сил трения);

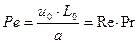– критерий Пекле (отношение интенсивностей конвективного и молекулярного переноса теплоты).

Величины, входящие в выражения для критериев, имеют следующий смысл:

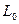– характерный размер или линейный масштаб потока, принимающий различные значения при разной геометрии движения (например, при движении жидкости в трубе это внутренний диаметр трубы, при свободной конвекции от горизонтальной трубы – это наружный диаметр трубы),м;

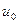– характерная скорость или масштаб скорости – также интерпретируемая по-разному при разной геометрии движения (например, при движении жидкости в трубе это средняя по сечению трубы скорость движения жидкости, а при внешнем обтекании трубы – это скорость жидкости вдали от поверхности трубы),м/с;

l – коэффициент теплопроводности жидкости, Вт/(м×К);

n – кинематический коэффициент вязкости жидкости, м²/с;

a – коэффициент температуропроводности жидкости, м²/с;

g – ускорение свободного падения, м/с²;

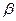– температурный коэффициент объемного расширения жидкости, К^-1;

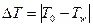– температурный напор (абсолютная величина разности температур жидкости и стенки), К.

Конкретный вид формул (8.2) и (8.3) зависит как от режима движения жидкости, так и от допущений, при которых производилась статистическая обработка экспериментальных данных (или приближенное аналитическое решение). В справочной литературе можно найти множество различных формул, относящихся к одним и тем же случаям теплоотдачи. Однако, как правило, все они дают близкие результаты. Так, например, в некоторых случаях критериальные зависимости (8.2) и (8.3) содержат множители, в которых учитываются неизотермичность среды вблизи поверхности, наличие участка неустановившегося движения и т.п.

В случае, если по горизонтальной трубе, помещенной в неподвижный воздух, течет жидкость, теплоотдача на внутренней поверхности трубы осуществляется посредством вынужденной конвекции, а на внешней – посредством свободной конвекции, при этом характерными размерами являются внутренний 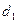и внешний 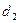диаметры трубы, соответственно.

При ламинарном течении (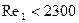) коэффициент теплоотдачи 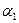может быть определен из выражения

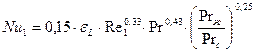, (8.4)

а при развитом турбулентном режиме (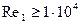) ­– из формулы Михеева

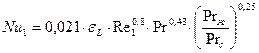(8.5)

где 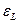– поправочный множитель, учитывающий вклад входного участка (его значения для разных значений числа 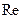и отношения 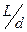приведены в Приложении 1V). Нижний индекс у критериев 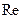и 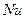в выражениях (8.4) и (8.5) показывает, что в качестве характерного размера в них фигурирует внутренний диаметр трубы 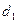. При этом все физические характеристики, входящие в критерии, вычисляются при средней температуре 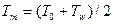жидкости вблизи поверхности, исключение составляет поправочный множитель 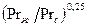, содержащий отношение чисел Прандтля жидкости вдали от поверхности 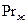и на самой поверхности 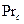, который учитывает изменение физических свойств жидкости в пристеночной области.

Теплоотдача на внешней поверхности трубы, происходящая посредством естественной конвекции, также может осуществляться в различных режимах. При малых температурных напорах (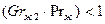) вокруг трубы образуется пленка нагретого воздуха. Этот режим называется пленочным. При этом

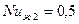, или 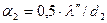, (8.6)

т.е. интенсивность теплообмена определяется теплопроводностью воздуха 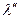. При увеличении температурного напора (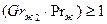) возможно разрушение ламинарного течения вокруг трубы. В этом случае расчет коэффициента теплоотдачи 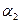на внешней поверхности трубы может быть произведен на основе соотношения

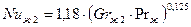. (8.7)

Нижние индексы у критериев в выражениях (8.6) и (8.7) показывает, что входящие в них теплофизические характеристики вычисляются при температуре жидкости вдали от твердой поверхности, а в качестве характерного размера в них фигурирует наружный диаметр трубы .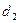

Процесс переноса тепла от одной текучей среды к другой через разделяющую их твердую перегородку называется теплопередачей. Например, при движении нагретой жидкости с температурой 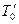в цилиндрической трубе, которую окружает воздух с температурой 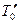, происходит теплопередача от жидкости к окружающему трубу воздуху через цилиндрическую стенку трубы. Этот процесс состоит из трех последовательных стадий:

· процесса теплоотдачи от жидкости к внутренней поверхности трубы, для которого величина теплового потока описывается выражением

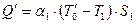, (8.8)

· процесса переноса тепла теплопроводностью через цилиндрическую стенку трубы, для которого величина теплового потока описывается выражением

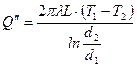, (8.9)

· и процесса теплоотдачи от наружной поверхности трубы к окружающему воздуху, для которого величина теплового потока описывается выражением

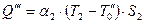. (8.10)

В приведенных формулах использованы следующие обозначения:

T₁, T₂ – температуры внутренней и наружной поверхностей цилиндрической трубы, соответственно, 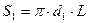и 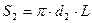- площади внутренней и наружной поверхностей цилиндрической трубы, соответственно, м²; l - коэффициент теплопроводности материала стенки трубы, Вт/(м×К); 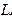- длина трубы, м.

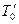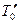Следует заметить, что, в отличие от температур текучих сред внутри и снаружи трубы – и – значения температур внутренней и наружной поверхностей цилиндрической трубы 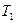и 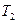не являются заданными (они зависят от теплового сопротивления различных стадий процесса передачи тепла).

В силу стационарности процесса теплопроводности

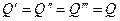. (8.11)

Подставляя (8.8), (8.9) и (8.10) в (8.11) и исключая неизвестные величины 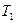и 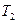, получаем

(8.12)

где величина

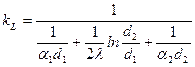(8.13)

называется линейным коэффициентом теплопередачи, Вт/(м×К).

Как правило, выражение (8.12) записывают для линейной плотности теплового потока Q_L=Q/L, Вт/м,представляющей собой величину теплового потока, приходящуюся на единицу длины трубы

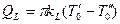. (8.14)

Именно величина 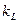характеризует интенсивность процесса теплопередачи. В общем случае, как это следует из формулы (8.13), она зависит как от интенсивности теплоотдачи (на внутренней и наружной поверхностях трубы), так и от интенсивности переноса тепла через стенку трубы за счет теплопроводности.

В случае, если величина l много больше, чем значение ln(d₂/d₁) (например, для меди l=390 Вт/(м×К)), можно записать:

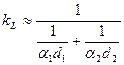(8.15)

Таким образом, для труб, выполненных из материала с хорошей теплопроводностью, лимитирующим звеном процесса теплопередачи оказываются процессы теплоотдачи на поверхностях стенки трубы.

Как правило, теплоотдача за счет вынужденной конвекции, осуществляющаяся на внутренней поверхности трубы, оказывается гораздо интенсивнее, чем теплоотдача за счет свободной конвекции, происходящая на наружной поверхности (в выражении для коэффициента теплопередачи (8.15) 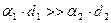). В этих условиях, когда лимитирующим звеном теплопередачи оказывается процесс теплоотдачи на наружной поверхности трубы, интенсификация именно этого процесса необходима для интенсификации теплопередачи в целом.

Одним из направлений такой интенсификации является оребрение наружной поверхности трубы. Предположим, что на внешнюю поверхность трубы нанесено 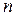ребер диаметром 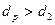и толщиной δ. Это приводит к тому, что площадь наружной поверхности в результате оребрения становится значительно больше, в соответствии с выражением

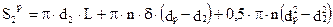(8.16)

Если ребра можно считать термически тонкими, оребренную поверхность можно считать изотермической. Поэтому в соответствии с выражением (8.15), линейный коэффициент теплопередачи через ребристую стенку можно представить в виде

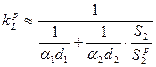, (8.17)

где величина 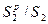называется коэффициентом оребрения.

Для экспериментального определения коэффициента теплопередачи необходимо знать изменение теплосодержания жидкости, протекающей в трубе, за единицу времени

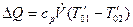. (8.18)

Для этого, как следует из (8.18), достаточно измерить объемный расход жидкости в трубе 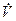, м³/с, и значения температуры жидкости во входном 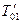и выходном 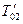сечениях трубы (средние по сечению), а также знать величину удельной теплоемкости жидкости при постоянном давлении 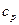, Дж/(м³×К).

Поскольку это изменение теплосодержания обусловлено теплопередачей, на основании закона сохранения энергии можно приравнять левые части выражений (8.12) и (8.18), что позволит получить необходимую расчетную формулу для коэффициента теплопередачи

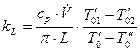. (8.19)

В силу стационарности процесса величина, описываемая выражением (8.18), может быть также приравнена величинам тепловых потоков на отдельных стадиях процесса теплопередачи, в частности, описываемым выражениями (8.8) и (8.10). Это позволяет, измеряя дополнительно температуру на внутренней поверхности трубы 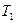и температуру на внешней поверхности трубы 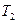, получить формулы для экспериментального определения коэффициентов теплоотдачи

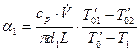, (8.20)

и

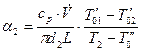. (8.21)

Дата добавления: 2015-06-27